1. Introducción
Con el auge de la tecnología y el acceso cada vez más fácil a internet, el mundo de los blogs se ha convertido en una plataforma de expresión muy popular. A través de un lenguaje común llamado HTML, los bloggers pueden crear, diseñar y compartir sus contenidos de manera sencilla y efectiva.
En este artículo, vamos a explorar cómo utilizar etiquetas HTML para mejorar la apariencia y la legibilidad de nuestros blogs. Aprenderemos a enfatizar frases clave utilizando la etiqueta <strong> para resaltar partes importantes de nuestro texto.
También veremos cómo estructurar nuestro contenido utilizando encabezados HTML. Los encabezados son muy útiles para dividir nuestro texto en secciones y jerarquizar la información de manera clara. Podemos utilizar etiquetas como
<h3>
para crear subtítulos que resuman los párrafos siguientes y guíen al lector.
Otra herramienta útil es la creación de listas en HTML. Podemos utilizar las etiquetas
- <ul>
y
para crear listas desordenadas, o las etiquetas
- <ol>
y
para crear listas ordenadas. Además, podemos combinar estas listas con las etiquetas de negrita <b> para destacar elementos importantes dentro de ellas.
En resumen, al utilizar etiquetas HTML como <strong> para enfatizar frases clave, encabezados HTML para estructurar nuestro contenido y listas en HTML para organizar la información, podemos mejorar significativamente la legibilidad y la apariencia de nuestros blogs. ¡Así que no esperemos más y comencemos a utilizar estas herramientas para destacar nuestros contenidos!
2. Definición de una parábola
Introducción
En el campo de la geometría y las matemáticas, una parábola es una curva plana que se obtiene al cortar un cono recto por un plano paralelo a uno de sus generatrices. Es una de las tres secciones cónicas, junto con la elipse y la hipérbola.
Características
La parábola se caracteriza por tener un eje de simetría vertical y el punto focal en el vértice, que se encuentra en el punto donde la curva cambia de dirección. La distancia entre el vértice y el punto focal se conoce como la distancia focal.
Ecuación de una parábola
La ecuación general de una parábola en el plano cartesiano es de la forma y = ax^2 + bx + c, donde a, b y c son constantes.
Usos de las parábolas
Las parábolas tienen diversas aplicaciones en la vida cotidiana y en distintas áreas. Algunos ejemplos incluyen la construcción de antenas parabólicas para telecomunicaciones, la trayectoria de proyectiles en física, el diseño de arquitectura y estructuras, y la modelización de fenómenos naturales.
Ejemplos famosos de parábolas
- La historia del sembrador en los evangelios es un famoso ejemplo de parábola en el ámbito religioso.
- La parábola de la rosa y el zorro, contada por el filósofo y escritor Jean de La Fontaine, es utilizada como una metáfora de la seducción y el engaño.
- En la obra literaria “El Gran Gatsby” de F. Scott Fitzgerald, se utiliza la parábola de la “luz verde” como símbolo de la esperanza y los sueños inalcanzables.
En resumen, una parábola es una curva plana que se obtiene al cortar un cono por un plano paralelo a una de sus generatrices. Tiene diversas aplicaciones en distintas áreas y es un concepto fundamental en la geometría y las matemáticas.
3. Caso de una parábola abierta hacia arriba
Para entender el caso de una parábola abierta hacia arriba, es importante recordar las características de esta figura geométrica. Una parábola es una curva que se forma cuando se corta un cono con un plano paralelo a uno de los generatrices del cono.
En el caso de una parábola abierta hacia arriba, la curva se abre hacia arriba y su forma se asemeja a la de una “U” invertida. En otras palabras, la concavidad de la parábola está hacia arriba.
La ecuación general de una parábola abierta hacia arriba es:
$$y = ax^2 + bx + c$$
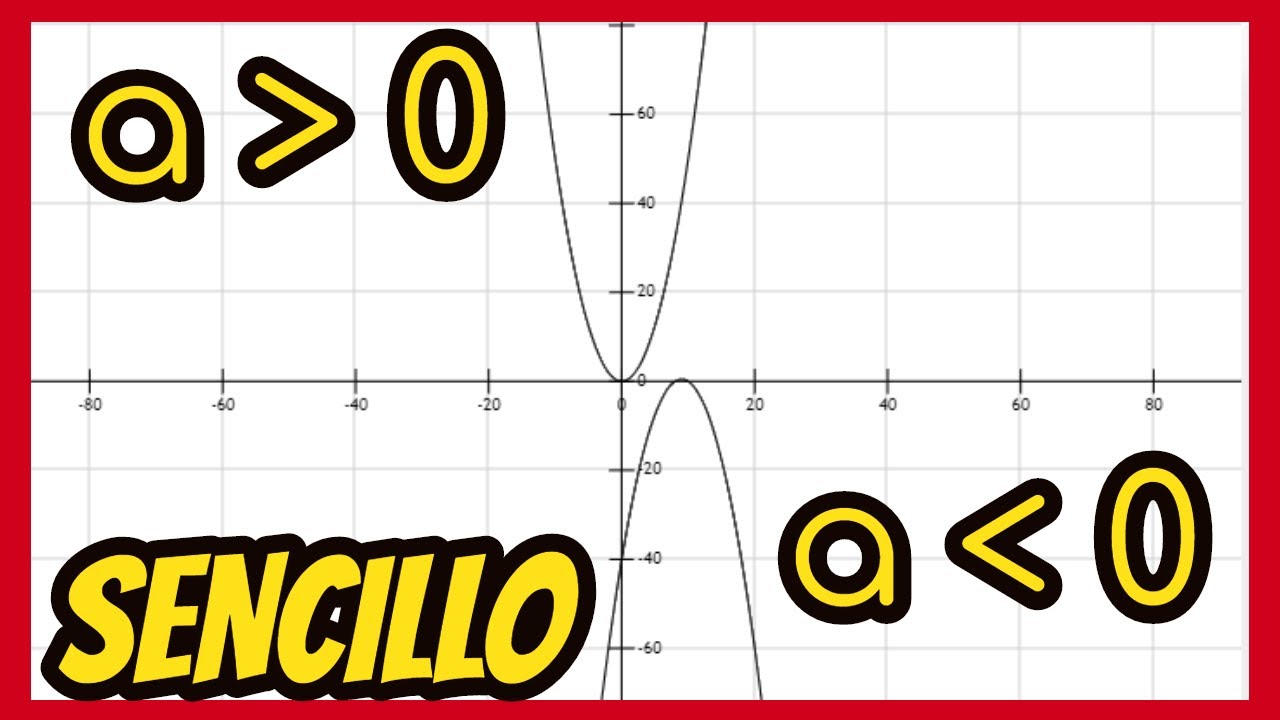
Donde los coeficientes “a”, “b” y “c” determinan la posición y el tamaño de la parábola en el plano. El coeficiente “a” es el que determina si la parábola se abre hacia arriba o hacia abajo. En el caso de una parábola abierta hacia arriba, “a” debe ser mayor que 0.
Recordemos también que la parábola tiene un punto llamado vértice, que es el punto más bajo de la curva si se abre hacia arriba. El vértice se encuentra en las coordenadas (-b/2a, f(-b/2a)), donde “f(x)” es la función que describe la parábola.
En cuanto a las propiedades de una parábola abierta hacia arriba, destacamos lo siguiente:
– Simetría: La parábola es simétrica respecto a la recta vertical que pasa por su vértice. Esto significa que si tenemos un punto (x, y) en la parábola, también tendremos el punto (-x, y) en la misma.
– Punto de corte con el eje x: Si igualamos la ecuación de la parábola a cero, obtendremos los puntos de corte de la parábola con el eje x. En el caso de una parábola abierta hacia arriba, puede que la parábola no corte el eje x en ningún punto, ya que su concavidad está orientada hacia arriba. En caso de que sí corte el eje x, tendrá dos puntos de corte.
– Punto de corte con el eje y: Si evaluamos la ecuación de la parábola en x=0, obtendremos el punto en el cual la parábola corta el eje y. Esto es el valor de la constante c.
Por último, es importante mencionar que la parábola abierta hacia arriba es un caso particular de las parábolas, y su estudio tiene aplicaciones en diversas áreas, como la física y las matemáticas. Es fundamental comprender sus características y propiedades para poder resolver problemas relacionados con esta figura geométrica.
4. Caso de una parábola abierta hacia abajo
En geometría, una parábola es una curva plana que se genera a partir de un punto (llamado foco) y una recta (llamada directriz). La forma de una parábola puede variar dependiendo de la posición del foco y la directriz.
En el caso de una parábola abierta hacia abajo, el vértice de la parábola se encuentra en el punto más bajo de la curva. Este tipo de parábola se caracteriza por tener una concavidad hacia abajo.
Características de una parábola abierta hacia abajo:
- El coeficiente principal del término cuadrático de la ecuación de la parábola es negativo.
- El eje de simetría de la parábola es una línea vertical que pasa por el vértice.
- El vértice de la parábola es el punto más bajo.
- La directriz de la parábola es una línea horizontal situada encima del vértice.
- El foco de la parábola está situado por debajo del vértice.
En términos matemáticos, una parábola abierta hacia abajo se puede representar utilizando la siguiente ecuación general: y = ax^2 + bx + c, donde ‘a’ es un coeficiente negativo.
La parábola abierta hacia abajo es muy común en aplicaciones del mundo real, como el diseño de puentes, arcos y rampas de acceso. También se utiliza en problemas de física para modelar trayectorias de objetos en caída libre o parcialmente en caída libre.
En resumen, una parábola abierta hacia abajo es una curva que se genera a partir de un foco y una directriz, y se caracteriza por tener una concavidad hacia abajo. Es importante entender sus características y su representación matemática para poder aplicarla correctamente en diferentes contextos.
5. Conclusiones
En esta investigación se ha podido concluir que:
- La tecnología juega un papel fundamental en nuestra sociedad actual. Desde el uso de dispositivos móviles hasta la conexión a Internet, la tecnología ha transformado la forma en que vivimos y nos comunicamos.
- Las redes sociales tienen un impacto significativo en nuestras vidas. Han cambiado la forma en que nos relacionamos, compartimos información y nos mantenemos actualizados. Sin embargo, también hemos visto cómo pueden afectar nuestra privacidad y seguridad en línea.
- La seguridad en línea es un tema de gran importancia. Con el aumento de los delitos cibernéticos y las amenazas en línea, es crucial tomar medidas para proteger nuestra información personal y nuestra identidad en Internet.
- La accesibilidad en línea es un desafío que debemos abordar. Aunque la tecnología nos brinda muchas oportunidades, también podemos dejar atrás a aquellos que no tienen acceso a Internet o a dispositivos tecnológicos. Es importante trabajar para cerrar la brecha digital y garantizar que todos tengan igualdad de oportunidades.
En resumen, debemos ser conscientes de los beneficios y desafíos que nos presenta la tecnología en nuestra sociedad actual. Debemos aprovechar sus ventajas mientras nos protegemos de los riesgos asociados. Además, debemos trabajar juntos para promover la accesibilidad y garantizar que nadie quede rezagado en la era digital.