¿Qué es una circunferencia inscrita en un triángulo?
Una circunferencia inscrita en un triángulo es una circunferencia que es tangente a los tres lados del triángulo.
Para que una circunferencia esté inscrita en un triángulo, su centro debe estar en el incentro del triángulo, que es el punto de intersección de las bisectrices de los ángulos del triángulo.
La circunferencia inscrita en un triángulo tiene varias propiedades interesantes. Una de ellas es que los segmentos que unen los vértices del triángulo con los puntos de contacto de la circunferencia inscrita en sus lados son bisectrices de los ángulos del triángulo.
También se puede demostrar que el área del triángulo es igual al producto del semiperímetro y el radio de la circunferencia inscrita, es decir, Área = Semiperímetro * Radio.
Además, el radio de la circunferencia inscrita en un triángulo está relacionado con las longitudes de los lados del triángulo a través de la fórmula:
Radio = Área / Semiperímetro
En resumen, una circunferencia inscrita en un triángulo es una circunferencia que es tangente a los tres lados del triángulo y tiene propiedades geométricas únicas que pueden ser utilizadas para resolver problemas relacionados con triángulos.
Propiedades de la circunferencia inscrita en un triángulo
La circunferencia inscrita en un triángulo tiene varias propiedades importantes que vale la pena destacar. Estas propiedades son las siguientes:
Centro
El centro de la circunferencia inscrita en un triángulo es el punto de intersección de las tres bisectrices de los ángulos del triángulo. Esta circunferencia es única y se denomina circunferencia inscrita.
Radio
El radio de la circunferencia inscrita en un triángulo se calcula utilizando la fórmula:
r = (área del triángulo) / (semiperímetro del triángulo)
Tangencia
La circunferencia inscrita en un triángulo es tangente a cada uno de los lados del triángulo. Esto significa que las líneas tangentes a la circunferencia en los puntos de tangencia son perpendiculares a los lados del triángulo.
Incentro
El incentro del triángulo es el punto donde se encuentra el centro de la circunferencia inscrita.
Relaciones de segmentos
La circunferencia inscrita en un triángulo también proporciona relaciones interesantes entre los segmentos del triángulo. Por ejemplo:
- La distancia desde el vértice de un triángulo hasta el punto de tangencia con la circunferencia es igual a la suma de las distancias desde ese vértice hasta los otros dos puntos de tangencia.
- El segmento de línea que une el punto de tangencia con la circunferencia con el vértice opuesto es perpendicular al lado correspondiente.
En resumen, la circunferencia inscrita en un triángulo es una figura geométrica importante que tiene varias propiedades clave. Estas propiedades incluyen el centro, el radio, la tangencia, el incentro y las relaciones de segmentos. Comprender estas propiedades puede ser útil en el estudio y análisis de triángulos.
Método para encontrar la ecuación de la circunferencia inscrita
En geometría, una circunferencia inscrita es aquella que se encuentra dentro de una figura geométrica, tangente a todos sus lados. En el caso particular de un triángulo, la circunferencia inscrita es aquella que pasa por los puntos de intersección de las bisectrices de los ángulos del triángulo.
Para encontrar la ecuación de la circunferencia inscrita en un triángulo, se puede utilizar el siguiente método:
- Encontrar las coordenadas de los vértices del triángulo. Esto se puede hacer utilizando las fórmulas para encontrar la distancia entre dos puntos.
- Calcular las longitudes de los lados del triángulo utilizando la fórmula de la distancia entre dos puntos.
- Calcular las coordenadas del centro de la circunferencia inscrita utilizando las fórmulas para encontrar el punto de intersección de las bisectrices de los ángulos del triángulo.
- Calcular el radio de la circunferencia inscrita utilizando la fórmula del radio de una circunferencia inscrita en un triángulo.
- Finalmente, utilizar la fórmula general de la ecuación de una circunferencia para obtener la ecuación de la circunferencia inscrita.
En resumen, el método para encontrar la ecuación de la circunferencia inscrita en un triángulo consiste en encontrar las coordenadas de los vértices del triángulo, calcular las longitudes de los lados, determinar las coordenadas del centro, calcular el radio y finalmente obtener la ecuación utilizando la fórmula general.
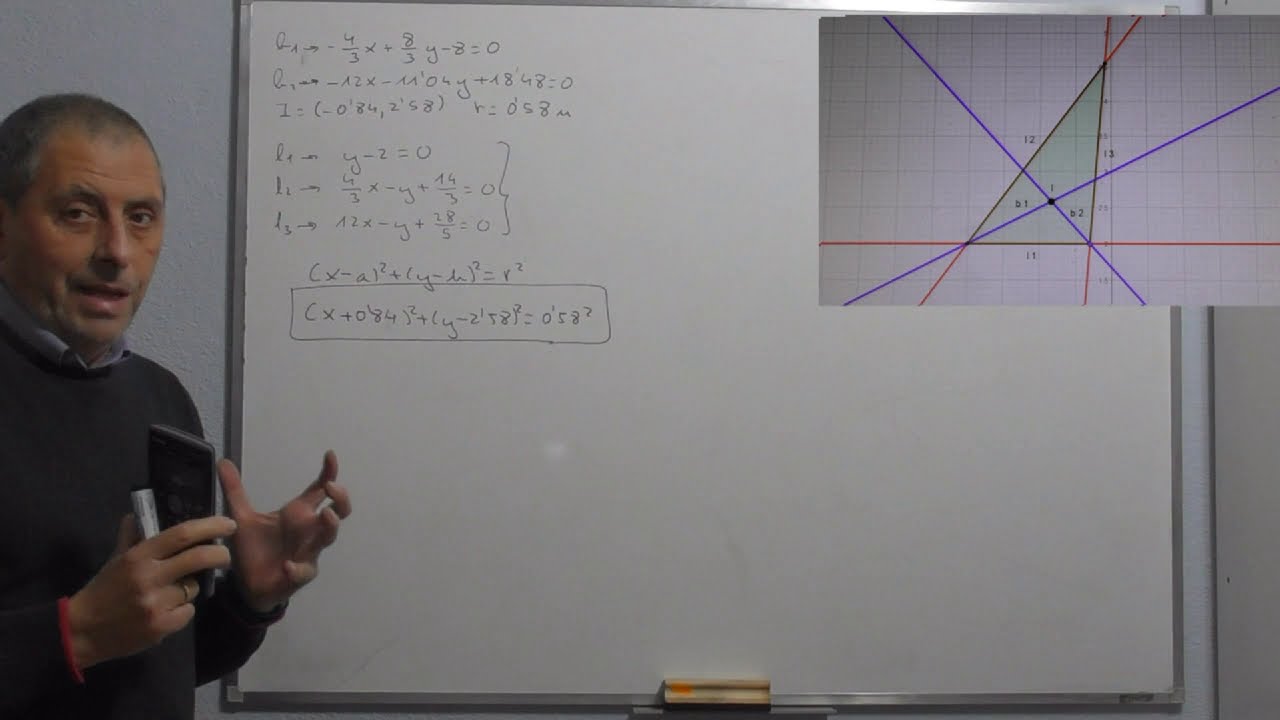
Ejemplo práctico: Resolviendo la ecuación de la circunferencia inscrita
En este ejemplo práctico, resolveremos la ecuación de la circunferencia inscrita en un triángulo. La circunferencia inscrita es una circunferencia que toca los tres lados del triángulo.
Supongamos que tenemos un triángulo ABC, donde AB, BC y AC representan los lados del triángulo. El objetivo es encontrar la ecuación de la circunferencia que toca los tres lados del triángulo simultáneamente.
Para resolver esta ecuación, necesitamos los puntos de intersección de las medianas del triángulo. Las medianas son segmentos que conectan cada vértice del triángulo con el punto medio del lado opuesto.
Paso 1:
Calcular las coordenadas de los puntos medios de los lados del triángulo.
Supongamos que las coordenadas de los vértices del triángulo son A(x1, y1), B(x2, y2) y C(x3, y3).
Las coordenadas del punto medio de AB se calculan promediando las coordenadas de A y B.
xm1 = (x1 + x2) / 2 ym1 = (y1 + y2) / 2
Las coordenadas del punto medio de BC se calculan promediando las coordenadas de B y C.
xm2 = (x2 + x3) / 2 ym2 = (y2 + y3) / 2
Las coordenadas del punto medio de AC se calculan promediando las coordenadas de A y C.
xm3 = (x1 + x3) / 2 ym3 = (y1 + y3) / 2
Paso 2:
Calcular las pendientes de las medianas.
La pendiente de la mediana que pasa por los puntos A y el punto medio de BC se calcula utilizando la fórmula:
m1 = (y1 - ym2) / (x1 - xm2)
De manera similar, podemos calcular las pendientes de las medianas que pasan por los puntos B y C, y los puntos A y C.
m2 = (y2 - ym3) / (x2 - xm3) m3 = (y1 - ym3) / (x1 - xm3)
Paso 3:
Encontrar las ecuaciones de las rectas que contienen las medianas.
Usando las pendientes calculadas en el paso anterior, podemos encontrar las ecuaciones de las rectas que contienen las medianas. La ecuación general de una recta es de la forma y = mx + b, donde m es la pendiente y b es la ordenada al origen.
Usando el punto medio de BC y la pendiente m1 calculada en el paso 2, la ecuación de la recta que contiene la mediana es:
y - ym2 = m1(x - xm2)
Calculamos de manera similar las ecuaciones de las rectas que contienen las medianas que pasan por los puntos B y C, y los puntos A y C.
y - ym3 = m2(x - xm3) y - ym1 = m3(x - xm1)
Paso 4:
Encontrar el punto de intersección de las rectas.
Resolviendo las ecuaciones de las rectas de manera simultánea, podemos encontrar el punto de intersección de las medianas. Las coordenadas de este punto se utilizan para encontrar la ecuación de la circunferencia inscrita.
Una vez que tenemos el punto de intersección, podemos usar la fórmula general de la ecuación de una circunferencia para encontrar la ecuación de la circunferencia inscrita.
La fórmula general de la ecuación de una circunferencia es de la forma (x – h)2 + (y – k)2 = r2, donde (h, k) representa las coordenadas del centro de la circunferencia y r es el radio.
Usando el punto de intersección como el centro de la circunferencia, encontramos el radio utilizando la distancia entre el centro y cualquier vértice del triángulo.
Una vez que tenemos el radio y las coordenadas del centro, podemos escribir la ecuación de la circunferencia inscrita.
En resumen, resolvemos la ecuación de la circunferencia inscrita en un triángulo encontrando los puntos de intersección de las medianas, y luego utilizando esas coordenadas para encontrar la ecuación de la circunferencia inscrita. Este ejemplo práctico muestra el proceso paso a paso para resolver esta ecuación.
Aplicaciones de la circunferencia inscrita en un triángulo
Una de las propiedades más interesantes de un triángulo es la existencia de una circunferencia inscrita en su interior. Para entender mejor las aplicaciones de esta circunferencia, es importante recordar que la circunferencia inscrita en un triángulo tiene su centro en el incentro del triángulo, el cual es el punto de intersección de las tres bisectrices de los ángulos del triángulo.
Relaciones entre los lados del triángulo y la longitud del radio
Una aplicación directa de la circunferencia inscrita en un triángulo es la relación entre los lados del triángulo y la longitud del radio de la circunferencia.
Por ejemplo, si consideramos un triángulo equilátero, en el cual todos los lados tienen la misma longitud, el radio de la circunferencia inscrita también tendrá la misma longitud que los lados del triángulo.
De manera más general, se puede demostrar que en cualquier triángulo, la longitud del radio de la circunferencia inscrita está relacionada con los lados del triángulo a través de la fórmula como r = abc / (4A), donde «r» es el radio de la circunferencia inscrita, «a», «b» y «c» son las longitudes de los lados del triángulo y «A» es el área del triángulo.
Propiedades de los ángulos del triángulo
Otra aplicación importante de la circunferencia inscrita es la relación entre los ángulos del triángulo y las medidas de los arcos que forman en la circunferencia.
En un triángulo, los ángulos opuestos a lados iguales tienen la misma medida. Esto implica que los arcos opuestos a lados iguales, y que corresponden a los ángulos del triángulo, también tienen la misma medida en la circunferencia inscrita.
Esta propiedad es especialmente útil en la resolución de problemas de geometría, ya que permite relacionar los ángulos del triángulo con las medidas de los arcos en la circunferencia inscrita, facilitando así los cálculos y demostraciones.
Intersección de las alturas del triángulo
La circunferencia inscrita en un triángulo también tiene relación directa con las alturas del triángulo. Las alturas de un triángulo corresponden a las perpendiculars trazadas desde cada vértice al lado opuesto.
Si trazamos las alturas de un triángulo y las prolongamos hasta que se intersecten, el punto de intersección se encuentra en la circunferencia inscrita. Este punto, llamado el ortocentro del triángulo, es de gran importancia en la geometría y tiene propiedades geométricas interesantes.
En resumen, la circunferencia inscrita en un triángulo tiene diversas aplicaciones en la geometría, relacionadas principalmente con las propiedades de los lados, ángulos y alturas del triángulo. Conocer estas aplicaciones permite resolver problemas geométricos de manera más eficiente y comprender mejor las propiedades fundamentales de los triángulos.