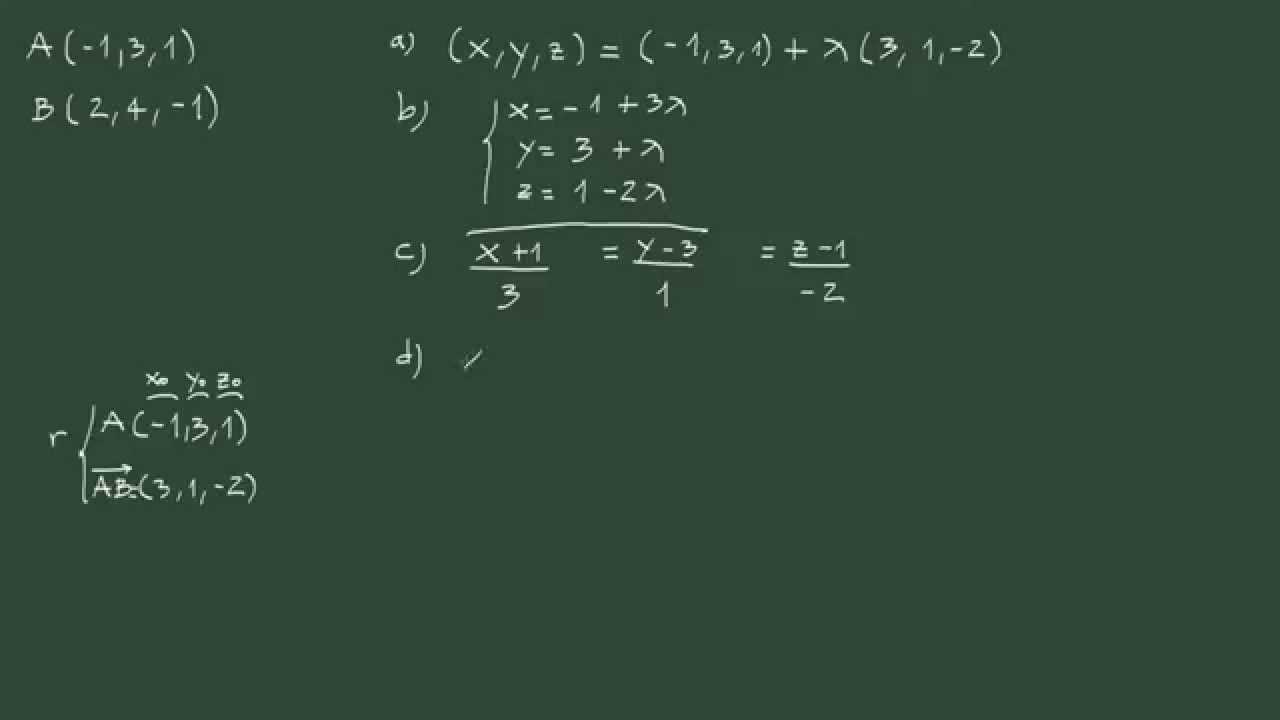En el mundo de la geometría tridimensional, encontrar la ecuación de una recta que pasa por dos puntos en el espacio tridimensional (R3) puede parecer un desafío intimidante al principio. Sin embargo, con un enfoque paso a paso y un entendimiento claro de los conceptos fundamentales, este proceso puede abordarse con confianza y éxito. En este artículo, exploraremos en detalle cómo identificar la ecuación de una recta en R3 que conecta dos puntos específicos, siguiendo un enfoque metódico que guiará a los lectores a través de cada paso crucial.
Cuando se trabaja en R3, es esencial comprender la representación geométrica de las rectas en este espacio tridimensional. A medida que nos sumergimos en el proceso de encontrar la ecuación de una recta que une dos puntos en R3, es útil recordar que la recta es una sucesión infinita de puntos que se extiende en ambas direcciones, y que cada punto en la recta se puede expresar como una combinación lineal de un punto base y un vector direccional. Manteniendo esta perspectiva en mente, nos adentraremos en el detalle de este fascinante proceso matemático.
Cómo identificar los puntos dados
Antes de calcular la ecuación de la recta que pasa por dos puntos en R3, el primer paso es identificar claramente las coordenadas de los dos puntos dados. Estos puntos se denotarán como P1(x1, y1, z1) y P2(x2, y2, z2), donde (x1, y1, z1) y (x2, y2, z2) representan las coordenadas de los puntos en el espacio tridimensional. Asegurarse de tener una comprensión clara y precisa de la ubicación de estos puntos es esencial antes de proceder con los cálculos para determinar la ecuación de la recta que los conecta.
Calcular el vector direccional
Una vez que se han identificado los puntos dados, el siguiente paso es determinar el vector direccional que define la dirección de la recta que conecta los puntos. El vector direccional, denotado como d = P2 – P1, se calcula restando las coordenadas del segundo punto dado (P2) de las coordenadas del primer punto dado (P1). Es importante recordar que este vector direccional representa la dirección y la pendiente de la recta en R3, y juega un papel crucial en la determinación de su ecuación.
Seleccionar un punto base
Después de calcular el vector direccional, el siguiente paso es elegir uno de los puntos dados como el punto base para la ecuación de la recta. Esta elección es fundamental, ya que el punto base se utilizará en la forma paramétrica de la ecuación de la recta, y su influencia se reflejará en la representación final de la recta en el espacio tridimensional.
Escribir la ecuación paramétrica de la recta
Con el vector direccional y el punto base claramente identificados, es hora de escribir la ecuación paramétrica de la recta que pasa por los dos puntos en R3. Utilizando la fórmula de la forma paramétrica de una recta en R3, que es r = P + td, donde r representa un punto genérico en la recta, P es el punto base, t es un parámetro real y d es el vector direccional de la recta, podemos construir la expresión paramétrica que describe la recta de manera concisa y precisa.
Escribir la ecuación simétrica de la recta
Además de la forma paramétrica, la ecuación simétrica de la recta que pasa por los dos puntos en R3 proporciona una representación alternativa que puede ser útil en ciertos contextos. La ecuación simétrica se expresa en términos de coordenadas cartesianas y permite una comprensión diferente de la recta en el espacio tridimensional, brindando una perspectiva adicional sobre su posición y dirección en relación con el sistema de ejes.
Verificar la validez de la ecuación
Una vez que se ha derivado la ecuación paramétrica y posiblemente la ecuación simétrica de la recta que conecta los dos puntos en R3, es fundamental verificar la validez de esta ecuación. Esta verificación implica asegurarse de que la ecuación obtenida realmente satisface las condiciones establecidas por los puntos dados y que representa una recta adecuada en el espacio tridimensional. La verificación cuidadosa brinda una capa adicional de certeza y comprensión en el proceso matemático.
Consideraciones adicionales y aplicaciones
Al abordar el desafío de encontrar la ecuación de una recta que pasa por dos puntos en R3, es crucial recordar que este concepto tiene diversas aplicaciones en campos como la geometría, la física y la ingeniería. Las rectas en R3 representan trayectorias, direcciones y relaciones espaciales, y comprender cómo determinar su ecuación es fundamental para una variedad de problemas del mundo real que involucran el espacio tridimensional.
Además, el proceso de encontrar la ecuación de una recta en R3 puede servir como un punto de partida para explorar conceptos más avanzados, como las intersecciones entre rectas, planos y superficies en el espacio tridimensional, lo que abre las puertas a una comprensión más profunda y completa de la geometría tridimensional. Al considerar estas aplicaciones más amplias, se revela la importancia y la relevancia de dominar el proceso de encontrar la ecuación de una recta en R3 que conecta dos puntos específicos.