1. Understanding the Concept of Dividing a Segment in a Given Ratio
When it comes to dividing a segment in a given ratio, it is important to have a clear understanding of the concept.
Dividing a segment in a given ratio means that we are splitting a line segment into two parts such that the ratio of their lengths is equal to the given ratio. This concept is commonly used in various fields including mathematics, engineering, and physics.
Why is it important to understand this concept?
Understanding the concept of dividing a segment in a given ratio allows us to solve problems involving proportions and ratios. It helps us determine the exact point at which to divide a line segment to achieve the desired ratio.
How do we divide a segment in a given ratio?
There are several methods to divide a segment in a given ratio, but one of the most commonly used methods is the use of a proportion.
Let’s say we have a line segment AB and we want to divide it in the ratio 2:3. To do this, we can set up a proportion using the lengths of the segments formed by the division:
- Let x be the length of the first segment.
- Then, the length of the second segment would be 2x.
- We can set up the proportion: AB / x = (AB – x) / 2x.
- Solving the proportion will give us the value of x, which can then be used to find the lengths of both segments.
Conclusion:
Dividing a segment in a given ratio is an important concept in mathematics and other fields. Understanding this concept allows us to solve problems involving proportions and ratios, and helps us determine the precise point at which to divide a line segment.
2. Identifying the Given Ratio and Segment Endpoints
When solving geometric problems involving ratios and segment endpoints, it is important to correctly identify the given information. This will allow you to apply the appropriate formulas or theorems to find the desired solution.
The given ratio refers to the relationship between the lengths of the segments involved. It can be written in the form of a fraction or a decimal. For example, a given ratio could be expressed as 2/3 or 0.5.
The segment endpoints are the points that define the ends of the segment. These endpoints are usually labeled with letters to distinguish them from other points. For example, the segment AB would have endpoints A and B.
To correctly identify the given ratio and segment endpoints, it is important to carefully read and analyze the problem statement. Look for any information about the lengths of the segments or any ratios provided. Additionally, identify any points that are labeled as endpoints or mentioned as part of the segment.
Once you have identified the given ratio and segment endpoints, you can proceed with solving the problem. This may involve using the given ratio to find the lengths of the segments or applying relevant theorems to find missing information.
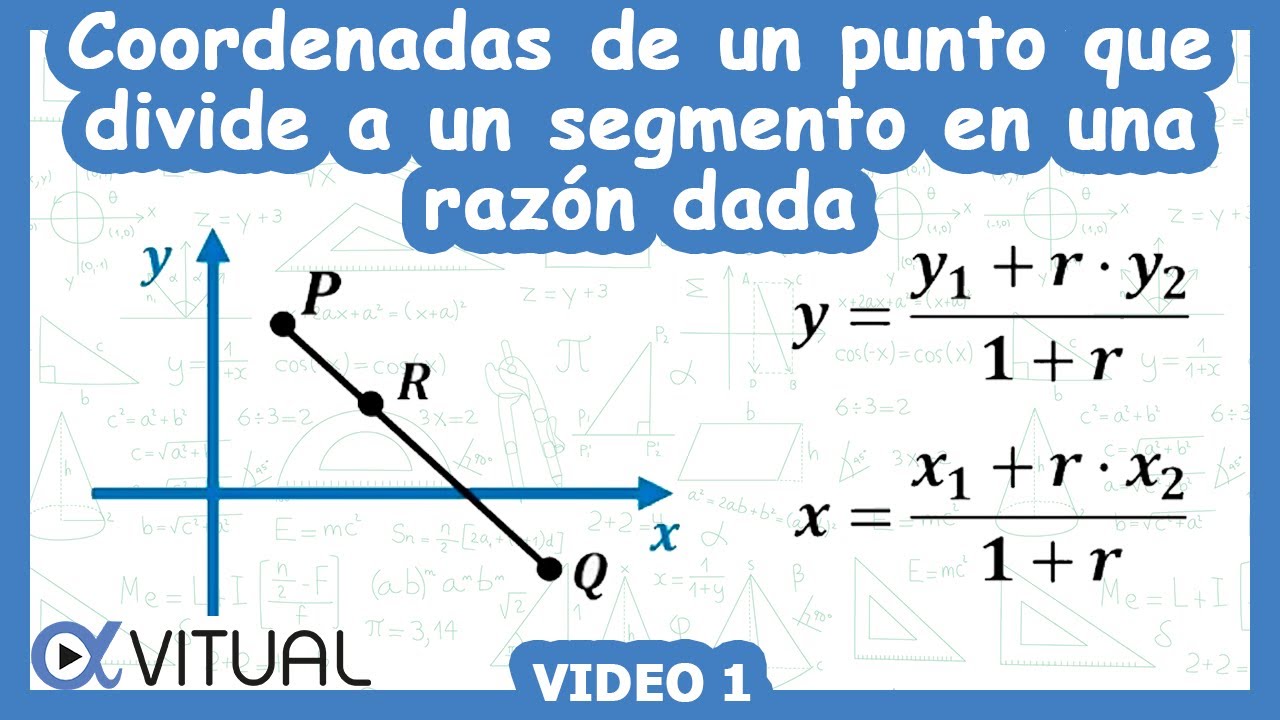
3. Applying the Section Formula
In previous posts, we have discussed various topics related to coordinate geometry. Today, we will delve deeper into the concept of the Section Formula.
The Section Formula is a fundamental concept in coordinate geometry that allows us to find the coordinates of a point that divides a line segment into a given ratio. This formula is widely used in various mathematical and real-life applications.
The Section Formula can be represented as:
[ frac{{x}}{{x_1}} = frac{{y}}{{y_1}} = frac{{m}}{{m+n}} ]
Here, (x) and (y) represent the coordinates of the point we want to find, while (x_1) and (y_1) represent the coordinates of one end of the line segment. (m) and (n) denote the ratio in which the line segment is divided.
Applying the Section Formula to Find Coordinates
Let’s walk through an example to better understand how the Section Formula works.
Suppose we have a line segment with endpoints A (3, 2) and B (9, 6), and we want to find the coordinates of a point P that divides the segment into a ratio of 3:1.
Using the Section Formula, we can calculate the coordinates of P:
[ frac{{x}}{{3}} = frac{{y}}{{1}} = frac{{3}}{{3+1}} ]
Simplifying the equation, we get:
[ frac{{x}}{{3}} = frac{{y}}{{1}} = frac{{3}}{{4}} ]
From the first two parts of the equation, we can determine that:
[ x = 3 times frac{{3}}{{4}} = frac{{9}}{{4}} ]
[ y = 1 times frac{{3}}{{4}} = frac{{3}}{{4}} ]
Thus, the coordinates of point P are (left(frac{{9}}{{4}}, frac{{3}}{{4}}right)).
In conclusion, the Section Formula is a powerful tool that allows us to find the coordinates of a point that divides a line segment in a given ratio. This formula can be used in various mathematical problems as well as real-life scenarios.
4. Solving a Sample Problem
Once you have a solid understanding of the problem and have analyzed the requirements, it’s time to start solving the sample problem. This step is crucial as it helps you determine the best approach to tackle similar problems in the future.
Identify the Problem:
First, analyze the given problem statement and understand what needs to be accomplished. Break down the problem into smaller tasks and identify any constraints or limitations.
Create a Plan:
Next, create a plan of action to solve the problem. This plan should outline the steps or algorithms you will follow to reach the desired outcome. Break down the problem further into subproblems if necessary.
Implement the Solution:
Once you have a clear plan, it’s time to implement the solution through coding. Use the programming language or tools that are most suitable for the problem at hand. Keep track of your progress and make sure to test your code as you go.
Test and Verify:
After the initial implementation, it’s crucial to test your solution by using sample inputs and comparing the outputs with the expected results. If any errors or bugs are found, debug and refine your code accordingly.
Analyze and Optimize:
Take the time to analyze the performance of your solution and see if there are any areas for improvement. Consider different test cases and edge scenarios to ensure the robustness of your code. If necessary, optimize your code for better efficiency.
Document the Solution:
Finally, it’s important to document your solution for future reference. This can include providing comments in the code, writing a summary of the approach used, and explaining any assumptions or trade-offs made during the problem-solving process.
By following these steps, you can effectively solve sample problems and improve your problem-solving skills. Remember to practice regularly and challenge yourself with different types of problems to continue growing as a developer.
5. Recap and Conclusion
As we near the end of this blog post, let’s take a moment to recap the key points discussed:
- HTML is a markup language used for creating the structure and content of web pages.
- H3 tags can be used to create subheadings within a section.
- Listas en HTML are a great way to organize information in a structured manner.
- The use of bold tags () can emphasize important words or phrases.
To conclude, HTML is a fundamental language for web development. By utilizing its various tags and elements, you can create well-structured and visually appealing web pages. Whether you’re a beginner or an experienced developer, understanding HTML is essential for creating engaging online content.
Thank you for reading this blog post, and we hope you found it informative. Feel free to leave any comments or questions below.