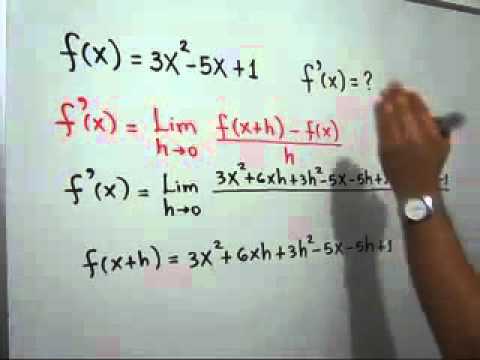Cómo obtener la derivada utilizando el límite

Introducción a la derivada utilizando el límite

La derivada es uno de los conceptos fundamentales en el cálculo diferencial. Permite medir la tasa de cambio instantánea de una función en un punto dado. En este artículo, exploraremos la introducción a la derivada utilizando el concepto de límite.

El límite

Antes de adentrarnos en la derivada, es importante entender el concepto de límite. El límite de una función describe el valor al que se acerca dicha función cuando su variable independiente se acerca a un cierto valor. Se utiliza una notación matemática específica para expresar el límite:

lim f(x) = L
x→a

Donde f(x) representa la función, L representa el límite y a es el punto al que la variable independiente se acerca.

El límite nos brinda información valiosa sobre el comportamiento de una función en un punto determinado. En el contexto de la derivada, utilizaremos el límite para calcular la tasa de cambio instantánea de una función en un punto.

La derivada

La derivada de una función describe la tasa de cambio instantánea de dicha función en un punto. Matemáticamente, se define como el límite de la razón incremental cuando el incremento en la variable independiente se acerca a cero:

f'(x) = lim [(f(x + h) - f(x)) / h]
h→0

Donde f'(x) representa la derivada de la función, f(x) es la función y h es el incremento en la variable independiente.

Para aquellos familiarizados con la geometría, la derivada también puede interpretarse como la pendiente de la recta tangente a la gráfica de la función en un punto dado. Es una medida instantánea de la inclinación de la curva en ese punto.

Aplicaciones de la derivada

La derivada tiene numerosas aplicaciones en diferentes campos de las matemáticas, la física y la ingeniería. Algunas de las aplicaciones comunes incluyen la optimización de funciones, la determinación de velocidades y aceleraciones instantáneas, el análisis de cambios en la economía, entre otros muchos campos donde se estudia el cambio y las tasas de cambio.

En resumen, la derivada es una herramienta poderosa para el análisis de funciones y el cálculo de tasas de cambio instantáneas. Utilizando el concepto de límite, podemos obtener información valiosa sobre el comportamiento de una función en un punto y aplicar este conocimiento en una amplia variedad de contextos.

Definición de la derivada

La derivada es un concepto fundamental en el cálculo diferencial. Se utiliza para representar la tasa de cambio instantáneo de una función en un punto específico.

La derivada de una función se representa mediante la notación f'(x) o dy/dx. Representa la pendiente de la recta tangente a la curva de la función en un punto dado.

La derivada se calcula utilizando el límite de diferenciales. Se toma la diferencia entre los valores de la función en dos puntos muy cercanos y se divide entre la diferencia de los valores de x correspondientes a esos puntos. A medida que estos dos puntos se acercan, la diferencia de los valores de x tiende a cero, lo que nos da la tasa de cambio instantánea de la función.

La derivada de una función nos proporciona información importante sobre su comportamiento. Nos indica si la función es creciente o decreciente en un intervalo determinado, si tiene máximos o mínimos locales, y nos ayuda a trazar el gráfico de la función.

Propiedades clave de la derivada

• Regla de la potencia: La derivada de una función potencial f(x^n) es n*x^(n-1).
• Regla de la constante: La derivada de una constante multiplicando a una función f(k*x) es k*f'(x).
• Regla de la suma y resta: La derivada de la suma o resta de dos funciones f(x) ± g(x) es f'(x) ± g'(x).
• Regla de la cadena: La derivada de una función compuesta h(g(x)) se calcula multiplicando la derivada externa por la derivada interna.

La derivada es una herramienta poderosa en matemáticas y ciencias físicas. Se utiliza en diversas aplicaciones como el cálculo de velocidades instantáneas, aceleraciones, optimizaciones y mucho más. Comprender y dominar la derivada es esencial para desarrollar habilidades en el cálculo diferencial.

Cálculo del límite para obtener la derivada

En cálculo, el proceso para obtener la derivada de una función a partir de su definición matemática se basa en el cálculo de límites. El límite es una herramienta fundamental que nos permite estudiar el comportamiento de una función en un punto específico. Para calcular el límite y obtener la derivada, se sigue un proceso paso a paso que nos permite encontrar la tasa de cambio instantánea de la función en un punto determinado.

Paso 1: Definir la función

El primer paso para calcular el límite y obtener la derivada es definir la función que queremos estudiar. Esta función puede ser cualquier expresión matemática que relacione una variable independiente con una variable dependiente. Por ejemplo, si queremos obtener la derivada de la función f(x) = x^2, debemos definir dicha función.

Para definir la función, podemos utilizar etiquetas HTML <h3> para resaltar el título y <p> para el contenido del párrafo.

Paso 2: Elegir el punto

Una vez que hemos definido la función, debemos elegir el punto en el cual queremos obtener la derivada. Este punto se representa usualmente como x=a, donde “a” es un número real que pertenece al dominio de la función. Al elegir el punto, estamos calculando la tasa de cambio instantánea de la función en ese punto.

Paso 3: Establecer la expresión límite

El siguiente paso es establecer la expresión límite que nos permitirá calcular la derivada de la función en el punto seleccionado. La expresión límite se define como el valor al cual se acercan los valores de la función cuando la variable independiente se acerca al punto seleccionado.

Para establecer la expresión límite, podemos utilizar etiquetas HTML <p> y <b> para resaltar las partes importantes de la explicación.

Paso 4: Calcular el límite

Una vez que hemos establecido la expresión límite, procedemos a calcular el límite. Para ello, utilizamos técnicas como factorización, racionalización, entre otras, que nos permiten simplificar la expresión y evaluarla en el punto seleccionado. El resultado obtenido será el valor del límite y, por lo tanto, la derivada de la función en ese punto.

Paso 5: Interpretar el resultado

Por último, interpretemos el resultado obtenido. La derivada representa la tasa de cambio instantánea de la función en un punto específico. Si el valor de la derivada es positivo, la función está creciendo en ese punto. Si el valor de la derivada es negativo, la función está disminuyendo en ese punto. Si el valor de la derivada es cero, la función tiene un punto crítico en ese punto.

En resumen, el cálculo del límite para obtener la derivada es un proceso fundamental en el campo del cálculo. A través de los pasos mencionados, podemos obtener información crucial sobre el comportamiento de una función en un punto específico.

Ejemplos de cálculo de la derivada utilizando el límite

En el cálculo diferencial, una de las herramientas fundamentales es el cálculo de la derivada de una función. Existen diferentes métodos para calcularla, y uno de los más comunes es utilizando el límite.

El cálculo de la derivada utilizando el límite consiste en encontrar la derivada de una función f(x) en un punto a, mediante el uso de la definición de derivada:

Para comprender mejor este concepto, veamos algunos ejemplos:

Ejemplo 1:

Calculemos la derivada de la función f(x) = x^2 en el punto a = 2 utilizando el límite.

1. Empecemos por expresar la definición de derivada:
Quizás también te interese:  Aprende sobre incrementos diferenciales y la regla de la cadena con una calificación de 4.7

f'(2) = lim [ f(x+h) – f(x) ] / h, cuando h tiende a 0.

2. Sustituimos la función f(x) = x^2 en la definición:

f'(2) = lim [ (x+h)^2 – 2^2 ] / h, cuando h tiende a 0.

3. Expandimos el cuadrado y simplificamos:

f'(2) = lim [ x^2 + 2hx + h^2 – 4 ] / h, cuando h tiende a 0.

4. Simplificamos la expresión:

f'(2) = lim [ 2x + h ] / h, cuando h tiende a 0.

5. Finalmente, evaluamos el límite cuando h tiende a 0:

f'(2) = 2x, evaluado en x = 2.

Por lo tanto, la derivada de la función f(x) = x^2 en el punto a = 2 es 4.

Ejemplo 2:

Calculemos la derivada de la función f(x) = sen(x) en el punto a = π/4 utilizando el límite.

1. Expresamos la definición de derivada:

f'(π/4) = lim [ f(x+h) – f(x) ] / h, cuando h tiende a 0.

2. Sustituimos la función f(x) = sen(x) en la definición:

f'(π/4) = lim [ sen(x+h) – sen(x) ] / h, cuando h tiende a 0.

3. Aplicamos la identidad trigonométrica de la resta de senos:

f'(π/4) = lim [ 2*cos((2x+h)/2)*sen(h/2) ] / h, cuando h tiende a 0.

4. Simplificamos la expresión:

f'(π/4) = lim [ cos((π/2+h)/2)*sen(h/2) ] / h, cuando h tiende a 0.

5. Finalmente, evaluamos el límite cuando h tiende a 0:

f'(π/4) = (√2/2) * 1 = √2/2.

En conclusión, el cálculo de la derivada utilizando el límite es una herramienta valiosa en el cálculo diferencial. Mediante la definición de derivada, podemos calcular la pendiente de una función en un punto específico. Estos ejemplos ilustran el proceso paso a paso para calcular la derivada utilizando el límite en diferentes funciones.

Aplicaciones de la derivada obtenida mediante el límite

La derivada obtenida mediante el límite tiene varias aplicaciones en diferentes campos. A continuación, mencionaremos algunas:

1. Análisis de funciones

La derivada nos permite analizar las propiedades de una función en un punto determinado. Por ejemplo, podemos utilizarla para determinar si una función es creciente o decreciente en un intervalo dado, identificar los puntos críticos de una función (donde la derivada es cero), encontrar los valores máximo y mínimo de una función, entre otros.

2. Estudio de la velocidad y aceleración

En física, la derivada se utiliza para estudiar la velocidad y aceleración de un objeto en movimiento. La velocidad instantánea de un objeto se obtiene a partir de la derivada de su posición respecto al tiempo, mientras que la aceleración se puede obtener a partir de la derivada de la velocidad respecto al tiempo.

3. Optimización de procesos

En ingeniería y economía, se utiliza la derivada para optimizar procesos y maximizar beneficios. Por ejemplo, en la producción de bienes, se busca maximizar la eficiencia y minimizar los costos, y la derivada nos ayuda a determinar los puntos críticos en los cuales se logra esto.

4. Estudio de las tasas de cambio

La derivada también se utiliza para analizar las tasas de cambio. Por ejemplo, en economía, se puede utilizar para calcular la elasticidad de demanda de un producto, que mide cómo cambia la demanda ante un cambio en el precio.

5. Modelado de fenómenos naturales

En ciencias naturales, la derivada se utiliza para modelar diversos fenómenos. Por ejemplo, en biología, se puede utilizar para modelar la tasa de crecimiento de una población o la velocidad de reacción en una reacción química.

Estas son solo algunas de las muchas aplicaciones de la derivada obtenida mediante el límite. Como se puede apreciar, la derivada es una herramienta fundamental en diferentes disciplinas y campos de estudio.