¿Qué es una elipse en geometría analítica?
Una elipse es una figura geométrica que se forma al cortar un cono con un plano en un ángulo oblicuo al eje del cono. En geometría analítica, una elipse puede ser descrita utilizando una ecuación en dos dimensiones.
La ecuación general de una elipse en el plano cartesiano es:
((x – h)^2) / a^2 + ((y – k)^2) / b^2 = 1
Donde (h, k) representa el centro de la elipse, ‘a’ es la longitud del semieje mayor y ‘b’ es la longitud del semieje menor.
Propiedades de una elipse:
- La suma de las distancias desde cualquier punto de la elipse a dos puntos fijos dentro de la misma, llamados ‘focos’, es constante. Esta propiedad se conoce como la propiedad de los focos de la elipse.
- Los puntos extremos de los ejes de la elipse se llaman ‘vértices’. Los vértices son puntos sobre la elipse que tienen una distancia fija al centro.
- La elipse tiene una simetría respecto a sus ejes. Esto significa que si tomamos cualquier punto sobre la elipse y lo reflejamos en el eje mayor o el eje menor, el nuevo punto también estará sobre la elipse.
La elipse tiene muchas aplicaciones en diferentes campos, como la astronomía, donde describe la forma de las órbitas planetarias, o en la arquitectura, donde se utiliza en el diseño de cúpulas y arcos.
Propiedades y características de la elipse en geometría analítica
En geometría analítica, la elipse es una figura plana definida como el lugar geométrico de todos los puntos cuya suma de distancias a dos puntos fijos (focos) es constante. Al estudiar las propiedades y características de la elipse, podemos destacar lo siguiente:
Ecuación de la elipse:
La ecuación general de la elipse en el plano cartesiano se puede expresar como:
(x – h)^2/a^2 + (y – k)^2/b^2 = 1
Donde (h, k) son las coordenadas del centro de la elipse, ‘a’ es la semianchura en el eje x y ‘b’ es la semianchura en el eje y.
Focos de la elipse:
Los dos puntos fijos que determinan la elipse se llaman focos. La distancia entre cada punto y cualquier punto de la elipse cumple la propiedad de que es constante y se denomina ‘c’.
Ejes y vértices:
La elipse tiene dos ejes: el eje mayor (2a) y el eje menor (2b). Los vértices son los puntos de intersección de la elipse con sus ejes.
Excentricidad:
La excentricidad (e) de la elipse es un valor que indica qué tan «aplanada» o «alargada» es la figura. Se calcula utilizando la fórmula e = c/a, donde ‘c’ es la distancia entre los focos y ‘a’ es la semianchura en el eje x.
Directrices:
Las directrices de la elipse son dos líneas paralelas al eje mayor que cumplen la propiedad de que la distancia de cualquier punto de la elipse a una directriz sumada con la distancia a la otra directriz es igual a la longitud del eje mayor (2a).
Simetría:
La elipse presenta simetría con respecto a sus ejes mayor y menor, lo que significa que si se traza una línea desde un punto en la elipse hasta el centro, y luego se traza una línea simétrica respecto a los ejes, ambas líneas tienen la misma longitud.
Estas son solo algunas de las propiedades y características de la elipse en geometría analítica. El estudio de esta figura geométrica tiene aplicaciones en diversas áreas como la astronomía, la ingeniería y la física.
Ecuación general de una elipse en geometría analítica
En geometría analítica, la ecuación general de una elipse se representa de la siguiente manera:
(x – h)^2 / a^2 + (y – k)^2 / b^2 = 1
Donde:
- (h, k) son las coordenadas del centro de la elipse.
- a es la distancia desde el centro hasta el vértice de la elipse en el eje horizontal.
- b es la distancia desde el centro hasta el vértice de la elipse en el eje vertical.
La elipse es una figura geométrica que se forma al cortar un cono por un plano inclinado que no llega a ser paralelo a las bases. La ecuación general representa todas las posibles ubicaciones de los puntos en la elipse.
En esta ecuación, los valores de (x, y) satisfacen la condición de que la suma de las distancias desde cualquier punto en la elipse hasta los dos focos es igual a una constante positiva. Estos focos son los puntos que se encuentran a una distancia c del centro de la elipse, donde c se calcula mediante la fórmula: c = sqrt(a^2 – b^2).
Además de la ecuación general, existen otras formas de representar una elipse, como la ecuación reducida o la ecuación paramétrica, que pueden ser más útiles en situaciones particulares.
La elipse tiene muchas aplicaciones en distintas áreas como la astronomía, la arquitectura y la ingeniería. Su simetría y propiedades hacen que sea una figura muy interesante de estudiar desde un punto de vista matemático.
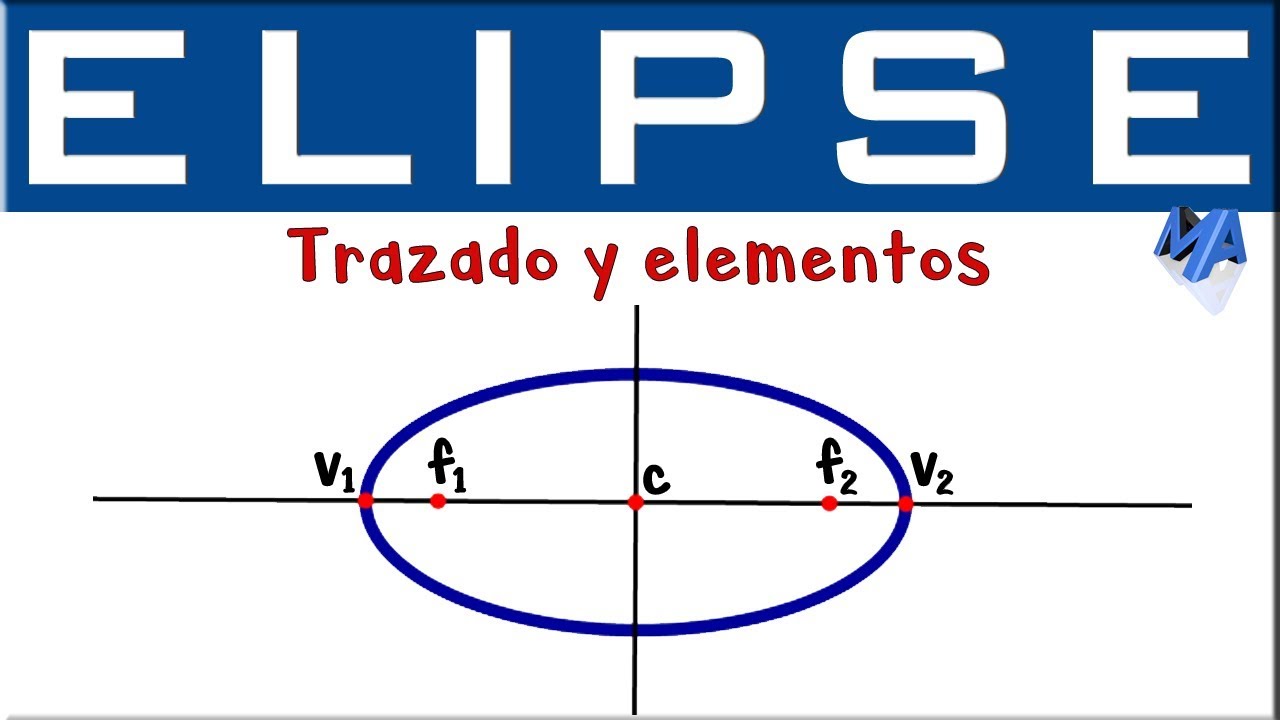
Elementos de una elipse en geometría analítica
El estudio de las elipses en geometría analítica es fundamental para comprender sus propiedades y aplicaciones en diversos campos. Una elipse está definida por varios elementos clave que nos permiten caracterizarla y analizarla en detalle.
Ejemplos de problemas resueltos sobre el concepto de elipse en geometría analítica
La elipse es una figura geométrica que se puede definir como el lugar geométrico de los puntos en un plano, tales que la suma de las distancias a dos puntos fijos llamados focos, siempre es constante.
Ejemplo 1:
Supongamos que tenemos una elipse con centro en el origen (0,0) de ecuación $frac{x^2}{a^2} + frac{y^2}{b^2} = 1$, donde a es la longitud del semieje mayor y b es la longitud del semieje menor.
Para encontrar el foco F1, utilizamos la fórmula $c = sqrt{a^2 – b^2}$, donde c es la distancia entre el centro y el foco F1.
Si a = 6 y b = 4, entonces c = $sqrt{36 – 16} = sqrt{20} = 2sqrt{5}$.
Por lo tanto, el foco F1 se encuentra en (2√5, 0).
Luego, podemos encontrar el segundo foco F2 sabiendo que F2 tiene las mismas coordenadas del foco F1 pero con signo negativo. Por lo tanto, el foco F2 se encuentra en (-2√5, 0).
Podemos comprobar esta solución trazando la elipse en un plano cartesiano.
Ejemplo 2:
Supongamos que tenemos una elipse con centro en (2,-3) de ecuación $frac{(x-2)^2}{9} + frac{(y+3)^2}{4} = 1$, donde a es la longitud del semieje mayor y b es la longitud del semieje menor.
Para encontrar los focos, utilizamos la misma fórmula c = $sqrt{a^2 – b^2}$.
En este caso, a = 3 y b = 2, entonces c = $sqrt{9 – 4} = sqrt{5}$.
Por lo tanto, los focos se encuentran en (2, -3 + √5) y (2, -3 – √5).
Ejemplo 3:
Supongamos que tenemos una elipse con centro en (-1,2) de ecuación $frac{(x+1)^2}{16} + frac{(y-2)^2}{25} = 1$, donde a es la longitud del semieje mayor y b es la longitud del semieje menor.
Para encontrar los focos, utilizamos la misma fórmula c = $sqrt{a^2 – b^2}$.
En este caso, a = 5 y b = 4, entonces c = $sqrt{25 – 16} = sqrt{9} = 3$.
Por lo tanto, los focos se encuentran en (-1, 2 + 3) y (-1, 2 – 3).
Estos son solo algunos ejemplos de problemas resueltos sobre el concepto de elipse en geometría analítica. La elipse es una figura con muchas propiedades interesantes y su estudio es fundamental en matemáticas.