La hipérbola, una de las curvas cónicas en geometría analítica, es un tema fundamental en matemáticas con una amplia gama de aplicaciones en la ciencia y la ingeniería. En este artículo, exploraremos en profundidad el concepto y las características de la hipérbola, desde su definición matemática hasta sus propiedades clave, brindándote una comprensión clara y detallada de este fascinante objeto geométrico.
Definición y Ecuación General de la Hipérbola
La hipérbola es el lugar geométrico de los puntos cuya diferencia de distancias a dos puntos fijos llamados focos es constante y mayor que la distancia entre los focos. En términos matemáticos, la hipérbola se puede definir mediante su ecuación general, que toma la forma:
donde $a$ y $b$ son constantes que determinan la forma y la orientación de la hipérbola. Esta ecuación revela la asimetría característica de la hipérbola, donde los ejes mayor y menor tienen longitudes diferentes.
Asíntotas de la Hipérbola
Una característica notable de la hipérbola son sus asíntotas. Estas son líneas rectas a las que se aproxima la curva a medida que nos alejamos hacia el infinito. La ecuación de las asíntotas de una hipérbola centrada en el origen es dada por $y = pmfrac{b}{a}x$, donde $a$ y $b$ son las semidistancias del eje transverso y conjugado, respectivamente.
Elementos Importantes de la Hipérbola
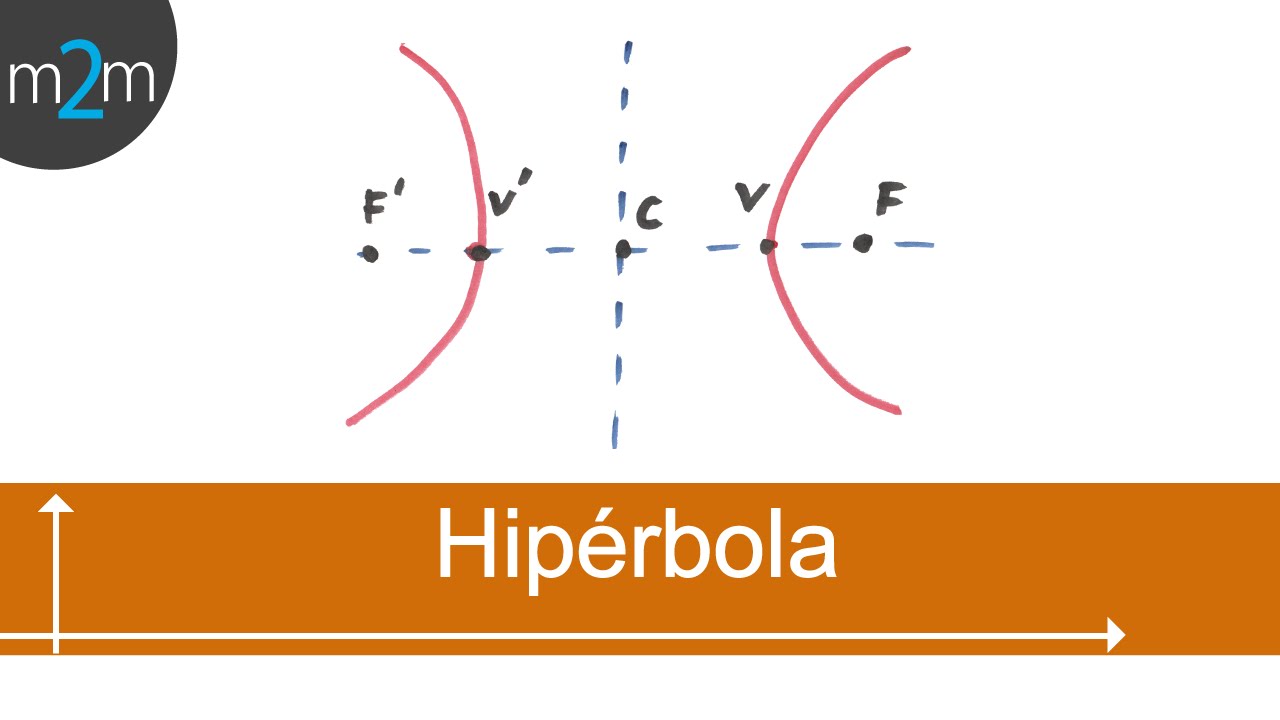
Además de sus focos y asíntotas, la hipérbola está definida por otros elementos importantes que ayudan a comprender su forma y posición en el plano cartesiano. El vértice de la hipérbola es el punto donde la curva cruza el eje transverso. Las distancias desde el centro de la hipérbola hasta los vértices son $pm a$ a lo largo del eje x. Los vértices también son el punto de intersección entre la hipérbola y sus ejes.
Ejes y Excentricidad
La hipérbola tiene dos ejes: el eje transverso, que se extiende entre los vértices, y el eje conjugado, que es perpendicular al eje transverso y pasa por el centro de la hipérbola. Además, la excentricidad de la hipérbola, denotada por $e$, es una medida de la forma en que la curva se desvía de ser circular. Para una hipérbola, la excentricidad se define como $e = sqrt{1 + frac{b^2}{a^2}}$.
Propiedades Asintóticas
Una propiedad crucial de la hipérbola es su comportamiento asintótico. A medida que nos alejamos hacia el infinito en cualquier dirección, la curva se aproxima a sus asíntotas, siguiendo un patrón predecible que ayuda a visualizar su forma y orientación en el plano cartesiano.
Intersecciones con los Ejes Coordinados
La hipérbola corta ambos ejes coordinados en puntos que determinan la posición y la orientación de la curva en el plano. Estos puntos de intersección proporcionan información esencial sobre la hipérbola y sus propiedades.
Ecuaciones Reducidas de la Hipérbola
Las ecuaciones reducidas de la hipérbola son formas alternativas de expresar la curva que simplifican su análisis y representación. Al reducir la forma general de la ecuación, obtenemos ecuaciones que nos permiten identificar rápidamente las características específicas de la hipérbola, como la ubicación de los focos, los vértices y otros elementos clave.
Hipérbolas con Centros Desplazados
Cuando la hipérbola tiene su centro en un punto distinto del origen, su ecuación general se complica ligeramente, pero sigue manteniendo sus propiedades distintivas. Las ecuaciones reducidas de hipérbolas con centros desplazados nos permiten estudiar y comprender la hipérbola en diferentes posiciones y orientaciones en el plano cartesiano.
Relación con la Geometría Euclidiana
La hipérbola desempeña un papel significativo en la geometría euclidiana, conectando conceptos fundamentales como las secciones cónicas, las transformaciones geométricas y las propiedades de los objetos geométricos en el plano. Al comprender la relación de la hipérbola con la geometría euclidiana, podemos apreciar su importancia en el amplio contexto matemático.
Transformaciones Lineales de la Hipérbola
Las transformaciones lineales, como las rotaciones y las traslaciones, pueden alterar la posición y la orientación de la hipérbola en el plano, manteniendo sus propiedades fundamentales. Estudiar estas transformaciones nos permite analizar cómo la hipérbola se comporta frente a cambios en su geometría subyacente.
Aplicaciones en Ciencia e Ingeniería
La hipérbola, al igual que otras curvas cónicas, tiene numerosas aplicaciones prácticas en campos tan diversos como la física, la ingeniería y la navegación. Su capacidad para modelar eficazmente ciertos fenómenos físicos la hace invaluable en la resolución de problemas del mundo real.
En la navegación por GPS, la hipérbola se utiliza para determinar la posición de un receptor mediante la medición de las diferencias de tiempo de llegada de las señales de varios satélites. Esta técnica, conocida como trilateración, se basa en la precisión matemática de la hipérbola para calcular ubicaciones con gran exactitud.
En resumen, la hipérbola es una curva cuyo estudio revela no solo propiedades matemáticas intrigantes, sino también aplicaciones prácticas vitales en la vida cotidiana. Comprender su estructura, características y relaciones con otros conceptos matemáticos es esencial para apreciar su amplio alcance en diversos campos de la ciencia y la ingeniería. Espero que este artículo te haya proporcionado una visión clara y enriquecedora de la hipérbola en geometría analítica.