¿El círculo unitario en la trigonometría?
La definición del círculo unitario es fundamental en el estudio de trigonometría. Este concepto es una herramienta clave que permite comprender y calcular las funciones trigonométricas de ángulos agudos. El círculo unitario se utiliza para visualizar las relaciones entre las coordenadas de un punto en una circunferencia de radio 1, su ángulo y las funciones trigonométricas.
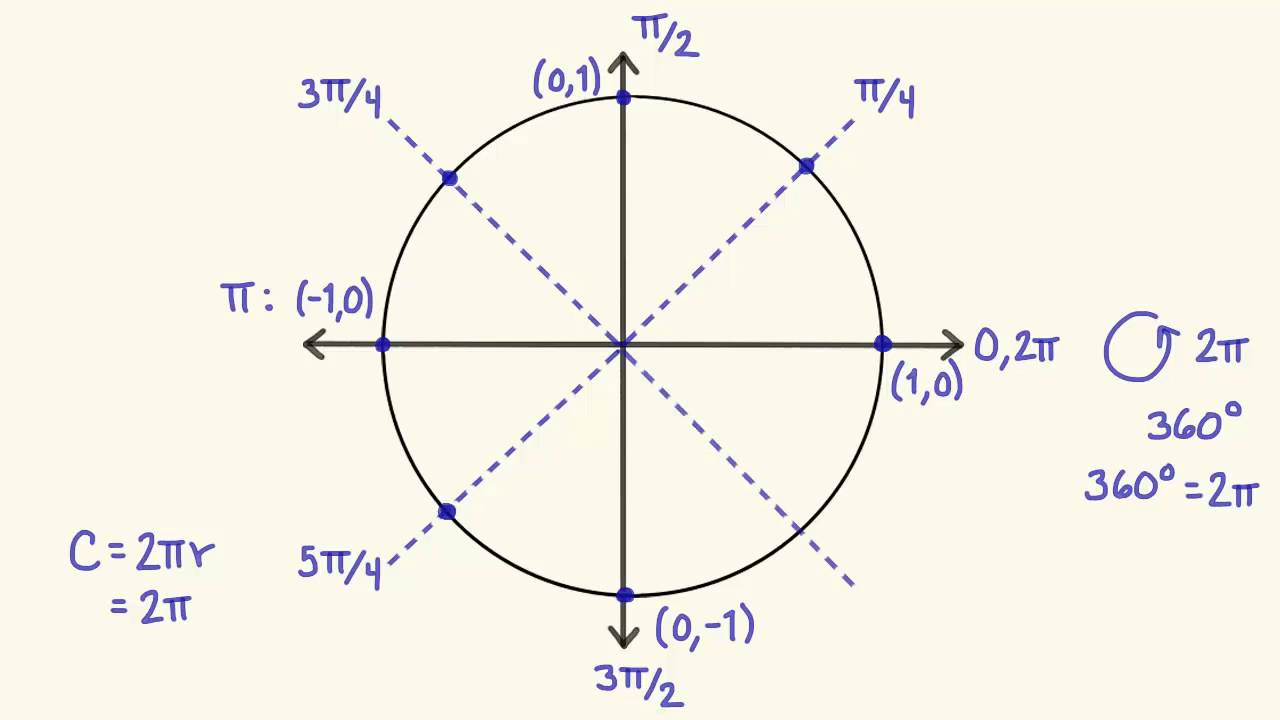
La representación del círculo unitario
El círculo unitario es una circunferencia de radio 1 centrada en el origen de un sistema de coordenadas cartesianas. Al trazar un ángulo en sentido contrario a las agujas del reloj a partir del eje x positivo, se puede ubicar un punto sobre la circunferencia. Este punto representa un ángulo y sus coordenadas (x, y) coinciden con las funciones trigonométricas seno y coseno del ángulo, respectivamente. Este enfoque proporciona una forma visual y conceptual de comprender las funciones trigonométricas y sus propiedades.
La conexión con las funciones trigonométricas
El círculo unitario establece una conexión directa entre las funciones trigonométricas y la geometría. Al trazar un ángulo a partir del eje x positivo y ubicar un punto sobre la circunferencia, se pueden determinar las coordenadas (x, y) de ese punto. Estas coordenadas representan los valores del coseno y el seno del ángulo respectivamente. De esta manera, el círculo unitario proporciona una visualización intuitiva de las funciones trigonométricas y de cómo varían con el cambio del ángulo.
Utilidad en cálculos de ángulos
El círculo unitario es una herramienta versátil que se utiliza para realizar cálculos trigonométricos con facilidad. Al conocer la relación entre las coordenadas de un punto en el círculo unitario y las funciones trigonométricas del ángulo correspondiente, es posible determinar rápidamente los valores de estas funciones para ángulos específicos. Esta capacidad resulta útil en diversas áreas, incluyendo la física, la ingeniería y las matemáticas aplicadas.
Relación con las identidades trigonométricas
El círculo unitario también proporciona un enfoque geométrico para comprender y demostrar las identidades trigonométricas. Al manipular triángulos en el círculo unitario, es posible establecer y demostrar las diversas identidades trigonométricas, lo que permite simplificar expresiones y resolver ecuaciones trigonométricas de manera más eficiente.
Aplicaciones en la resolución de problemas
Cuando se abordan problemas que involucran ángulos y funciones trigonométricas, el círculo unitario brinda una herramienta visual poderosa para comprender y resolver dichos problemas. La representación geométrica de los ángulos y las funciones trigonométricas en el círculo unitario permite abordar situaciones prácticas con mayor claridad y facilita la interpretación de los resultados obtenidos.
Interpretación de las funciones trigonométricas
El círculo unitario ofrece una perspectiva única para interpretar las funciones trigonométricas. Al trazar ángulos y relacionar sus coordenadas en el círculo unitario con las funciones seno y coseno, es posible comprender la relación entre los ángulos y los valores de estas funciones. Esta interpretación geométrica permite visualizar cómo varían las funciones trigonométricas y su comportamiento en relación con los ángulos.
Relación con otras áreas de las matemáticas
Además de su relevancia en trigonometría, el círculo unitario tiene conexiones con otras áreas de las matemáticas, como el cálculo, el álgebra y la geometría analítica. Su capacidad para visualizar y relacionar conceptos trigonométricos lo convierte en una herramienta fundamental en diversos contextos matemáticos, contribuyendo a una comprensión más profunda de los temas relacionados.
Abstracción del concepto
A pesar de ser un concepto geométrico, el círculo unitario también puede ser interpretado de manera abstracta como un enfoque algebraico de las funciones trigonométricas. Esta abstracción permite utilizar sus propiedades para resolver ecuaciones, graficar funciones y analizar patrones matemáticos de manera más general.
En resumen, el círculo unitario es un concepto fundamental en la trigonometría que proporciona una representación geométrica de las funciones trigonométricas y sus relaciones con los ángulos. Su utilidad en el cálculo de valores trigonométricos, la demostración de identidades y la resolución de problemas prácticos demuestra su relevancia en diferentes contextos matemáticos y aplicaciones en disciplinas científicas. Mediante su comprensión y aplicación, el círculo unitario ofrece una perspectiva visual y conceptual poderosa que enriquece el estudio de la trigonometría y otras áreas de las matemáticas.