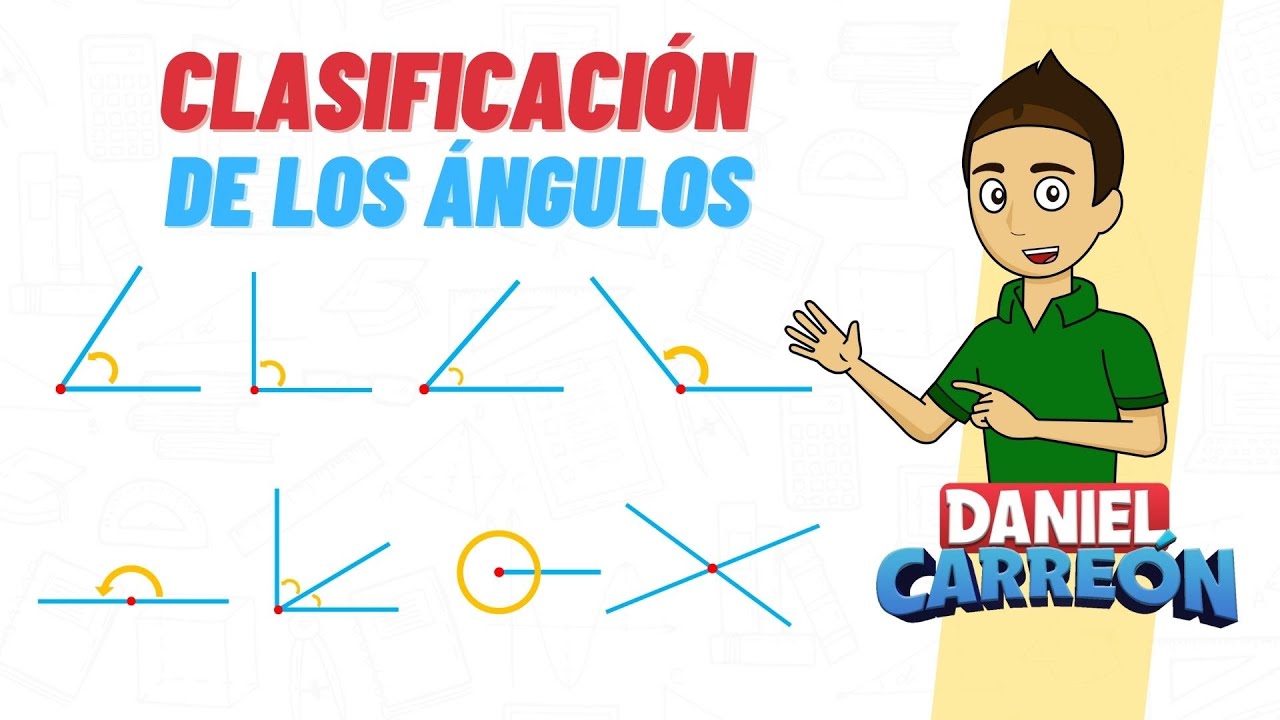
1. ¿Qué es un ángulo?
Un ángulo es la figura formada por dos rayos que tienen un punto común llamado vértice. Los rayos se llaman lados del ángulo y el vértice es el punto de unión de los dos lados. Los ángulos se miden en grados.
Existen diferentes tipos de ángulos:
- Ángulo agudo: es aquel que mide menos de 90 grados.
- Ángulo recto: es aquel que mide exactamente 90 grados.
- Ángulo obtuso: es aquel que mide más de 90 grados pero menos de 180 grados.
- Ángulo llano: es aquel que mide exactamente 180 grados.
- Ángulo completo: es aquel que mide exactamente 360 grados.
Los ángulos son utilizados en diversos campos, como la geometría, la trigonometría y la física. Son fundamentales para medir y describir la relación entre diferentes direcciones o posiciones.
2. Tipos de ángulos según su medida
Existen varios tipos de ángulos según su medida:
Ángulo agudo:
Es aquel que mide menos de 90 grados.
Ángulo recto:
Es aquel que mide exactamente 90 grados.
Ángulo obtuso:
Es aquel que mide más de 90 grados pero menos de 180 grados.
Ángulo llano:
Es aquel que mide exactamente 180 grados.
Ángulo completo:
Es aquel que mide exactamente 360 grados.
Es importante recordar que la medida de un ángulo se expresa en grados y se representa con el símbolo º.
¡Espero que esta información te haya sido útil!
3. Tipos de ángulos según su posición
En geometría, los ángulos son una medida de la separación entre dos líneas o planos que se cruzan en un punto común. Dependiendo de su posición, los ángulos pueden clasificarse en diferentes tipos:
Ángulos agudos:
Los ángulos agudos son aquellos cuya medida es menor a 90 grados. Estos ángulos suelen ser más pequeños y se encuentran en la parte inferior izquierda del vértice.
Ángulos obtusos:
Los ángulos obtusos son aquellos cuya medida es mayor a 90 grados pero menor a 180 grados. Estos ángulos se encuentran en la parte superior izquierda del vértice.
Ángulos rectos:
Los ángulos rectos son aquellos cuya medida es exactamente 90 grados. Estos ángulos forman una “L” y se encuentran en la parte inferior derecha del vértice.
Ángulos llanos:
Los ángulos llanos son aquellos cuya medida es exactamente 180 grados. Estos ángulos forman una línea recta y se encuentran en la parte superior derecha del vértice.
Conociendo los diferentes tipos de ángulos según su posición, es posible identificar y clasificar los ángulos en problemas y situaciones geométricas.
4. Ángulos complementarios y suplementarios
En geometría, los ángulos complementarios y suplementarios son conceptos importantes relacionados con la medida de los ángulos. Estos términos se utilizan para describir la relación entre dos ángulos.
Ángulos complementarios: Dos ángulos son complementarios si la suma de sus medidas es igual a 90 grados. En otras palabras, cuando se colocan uno junto al otro, forman un ángulo recto. Por ejemplo, si un ángulo mide 30 grados, su complementario medirá 60 grados.
Ángulos suplementarios: Dos ángulos son suplementarios si la suma de sus medidas es igual a 180 grados. En este caso, cuando se colocan uno junto al otro, forman una línea recta. Por ejemplo, si un ángulo mide 120 grados, su suplementario medirá 60 grados.
Una forma sencilla de recordar la diferencia entre los ángulos complementarios y suplementarios es pensar en el ángulo recto (90 grados) como “completo” y el ángulo recto doble (180 grados) como “suplementario”.
Es importante tener en cuenta que los ángulos complementarios y suplementarios no tienen que estar uno al lado del otro. Pueden estar en diferentes partes de una figura o incluso en diferentes figuras. Lo único que importa es que la suma de sus medidas cumpla con la definición de complementario o suplementario.
Ejemplos de ángulos complementarios:
- 35 grados y 55 grados
- 20 grados y 70 grados
- 45 grados y 45 grados
Ejemplos de ángulos suplementarios:
- 100 grados y 80 grados
- 150 grados y 30 grados
- 75 grados y 105 grados
En resumen, los ángulos complementarios son aquellos cuya suma es igual a 90 grados, mientras que los ángulos suplementarios tienen una suma de 180 grados. Estos conceptos son fundamentales en geometría y son útiles para el diseño y la resolución de problemas relacionados con ángulos.
5. Ángulos congruentes
En geometría, los ángulos congruentes son aquellos que tienen la misma medida. Es decir, si dos ángulos tienen la misma apertura, entonces se consideran congruentes.
Para demostrar que dos ángulos son congruentes, se pueden utilizar diferentes métodos. Uno de ellos es la comparación directa de las medidas de los ángulos. Si dos ángulos tienen la misma medida, se pueden afirmar que son congruentes.
Otro método común para demostrar la congruencia de dos ángulos es a través de la aplicación de teoremas y postulados geométricos. Por ejemplo, el teorema de los ángulos suplementarios establece que si la suma de dos ángulos es igual a 180 grados, entonces los ángulos son congruentes. También, el teorema de los ángulos correspondientes establece que si dos líneas paralelas son cortadas por una transversal, entonces los ángulos correspondientes son congruentes.
La congruencia de ángulos puede tener diversas aplicaciones en geometría. Por ejemplo, es utilizada en la demostración de teoremas y en la resolución de problemas geométricos. También, es fundamental en la construcción de figuras geométricas, ya que la congruencia de ángulos permite construir triángulos y cuadriláteros con medidas exactas.
En resumen, los ángulos congruentes son aquellos que tienen la misma medida. Su demostración puede realizarse mediante la comparación de sus medidas o a través de la aplicación de teoremas y postulados geométricos. La congruencia de ángulos es utilizada en la demostración de teoremas, en la resolución de problemas geométricos y en la construcción de figuras geométricas.