Concepto de monomios y polinomios
Los monomios y polinomios son conceptos fundamentales en el álgebra y las matemáticas. Comprender la diferencia entre ellos es esencial para desarrollar una base sólida en este campo. A menudo, se confunden entre sí, pero en realidad presentan diferencias significativas que vale la pena explorar.
¿Qué es un monomio?
Un monomio es una expresión algebraica compuesta por el producto de un coeficiente numérico y una o más variables elevadas a exponentes enteros no negativos. Por ejemplo, 2x, 3xy, o 4x2 son monomios. Los monomios pueden contener una única variable o múltiples variables, pero en todos los casos, los exponentes deben ser números enteros positivos. Al estudiar monomios, es crucial comprender que una constante sola también se considera un monomio, ya que puede expresarse como el producto de la constante y la variable elevada a cero, considerando x0 = 1.
Características de un monomio
Los monomios presentan algunas características clave que los distinguen en el ámbito algebraico. Primero, el grado de un monomio es la suma de los exponentes de las variables. Por ejemplo, el monomio 5x2y3 tiene un grado de 5, ya que la suma de 2 y 3 es 5. Además, es importante destacar que un monomio también puede tener un coeficiente fraccional, como 1/2x2. Esta variabilidad en los coeficientes es una de las particularidades de los monomios.
¿Qué es un polinomio?
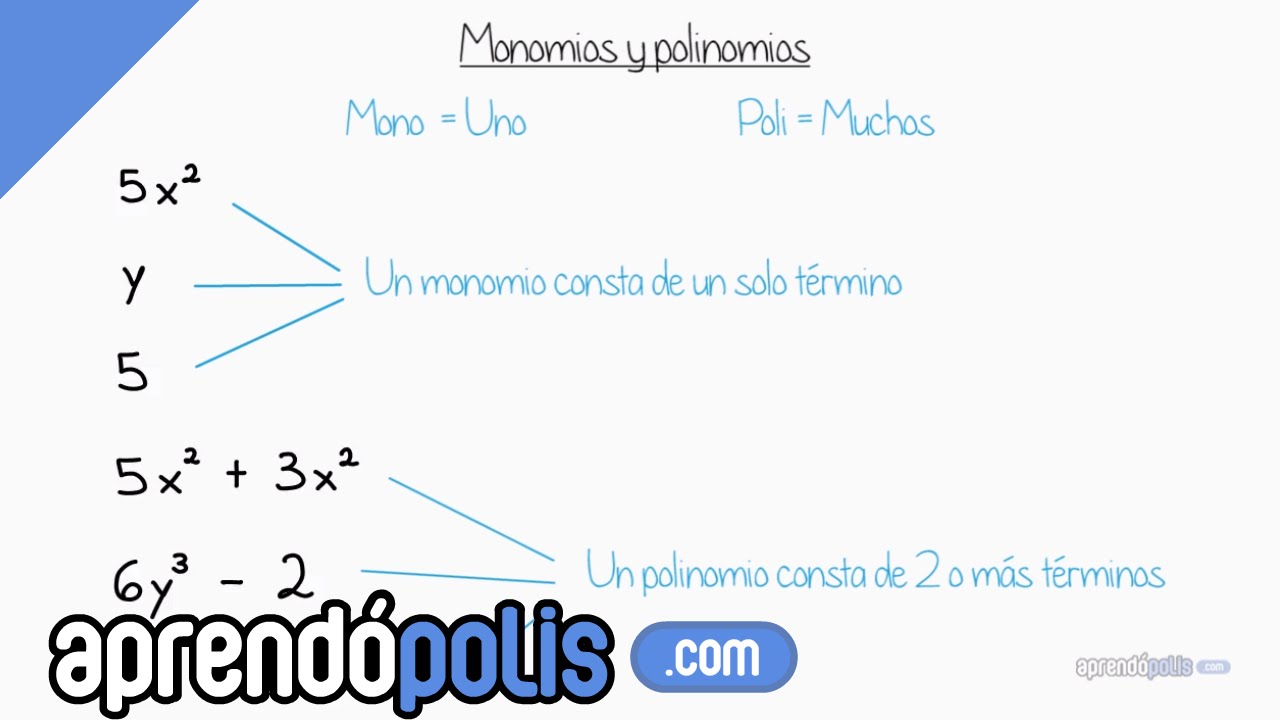
Un polinomio es una expresión algebraica que consiste en la suma de uno o más monomios. Esta suma puede incluir términos que varían en el número de variables y en los grados de las mismas. Por ejemplo, 2x + 3xy + 4x2 es un polinomio. Es vital comprender que cada término dentro de un polinomio puede ser un monomio por separado, pero al sumarlos, forman un polinomio.
Grado de un polinomio
El grado de un polinomio se determina tomando el término con el mayor exponente de las variables y sumándolo. Por ejemplo, en el polinomio 2x + 3xy + 4x2, el término de grado más alto es 4x2, lo que da como resultado un polinomio de grado 2. Este concepto es crucial para comprender y clasificar los polinomios en función de su complejidad y número de términos.
Diferencias clave entre monomios y polinomios
A pesar de que tanto los monomios como los polinomios están compuestos por variables y coeficientes, presentan diferencias significativas que los distinguen entre sí. La diferencia principal radica en la cantidad de términos que los componen: los monomios contienen un solo término, mientras que los polinomios contienen múltiples términos que se suman entre sí. Esta distinción es crucial para comprender la naturaleza y el alcance de cada uno de estos elementos algebraicos.
Ejemplos ilustrativos
Para comprender más claramente estas diferencias, consideremos los siguientes ejemplos:
El monomio 3x2 tiene un solo término y, por lo tanto, es clasificado como un monomio. Por otro lado, el polinomio 2x + 3xy + 4x2 consta de tres términos que se suman entre sí, lo que lo convierte en un polinomio. Esta distinción entre la cantidad de términos es fundamental para diferenciar entre monomios y polinomios en situaciones prácticas.
Aplicaciones en contextos reales
Los monomios y polinomios juegan un papel crucial en la resolución de problemas matemáticos y en un amplio abanico de aplicaciones en la vida cotidiana. Desde determinar áreas y volúmenes en geometría hasta modelar fenómenos físicos o económicos, estas expresiones algebraicas son fundamentales para comprender y resolver una amplia gama de situaciones cotidianas.
Desarrollo tecnológico
En el ámbito tecnológico, los monomios y polinomios son utilizados en algoritmos de procesamiento de imágenes, técnicas de compresión de datos y en las bases de los algoritmos de inteligencia artificial y aprendizaje automático. Comprender las diferencias y aplicaciones de monomios y polinomios es crucial para avanzar en estas áreas y desarrollar soluciones innovadoras y eficientes.
Importancia en las ciencias naturales
En las ciencias naturales, los monomios y polinomios se utilizan para modelar fenómenos físicos y químicos. Desde la descripción de trayectorias de partículas hasta la formulación de ecuaciones que describen el comportamiento de reacciones químicas, estas expresiones algebraicas desempeñan un papel fundamental en el avance y la comprensión de las ciencias naturales.
En resumen, los monomios y polinomios son conceptos fundamentales en el ámbito algebraico y matemático. Si bien comparten similitudes en términos de variables y coeficientes, presentan diferencias críticas en cuanto a la cantidad de términos que los componen. Comprender estas diferencias es crucial para avanzar en el estudio y la aplicación de expresiones algebraicas en contextos académicos y prácticos, ya que permiten abordar una amplia gama de problemas y situaciones de forma eficiente y precisa.