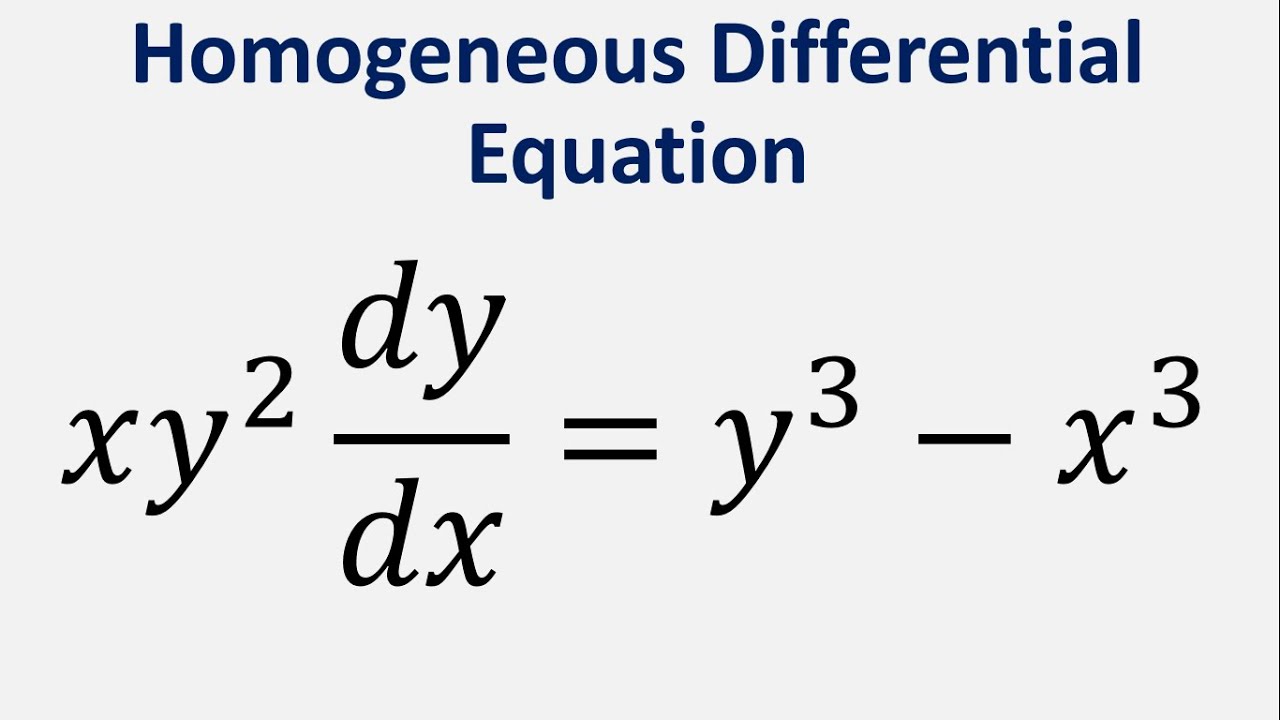En este artículo, exploraremos la ecuación diferencial no lineal de primer orden representada por la expresión xy^2 dy/dx = y^3 – x^3. Esta ecuación, aunque aparentemente compleja, puede desglosarse mediante diversos métodos para encontrar su solución. A lo largo de este artículo, abordaremos paso a paso cómo resolver esta ecuación diferencial y comprender su significado en el contexto matemático.

Anuncios

Entendiendo la ecuación diferencial

Antes de abordar la resolución de la ecuación diferencial, es crucial comprender su estructura y significado. Esta ecuación implica una derivada de y con respecto a x, multiplicada por la función y^2, y esta expresión es igual a la diferencia entre y^3 y x^3. Esta forma diferencial no lineal puede presentar desafíos únicos en su resolución, pero con los enfoques correctos, podemos desentrañar su solución de manera efectiva.

Método de separación de variables

Un enfoque inicial para abordar esta ecuación diferencial implica el método de separación de variables. Dividimos la ecuación en dos lados y reorganizamos los términos para agrupar las variables x e y por separado. Luego, se integran ambos lados de la ecuación para alcanzar una solución general.

Anuncios

Paso 1: Desglose de la ecuación

Comenzamos descomponiendo la ecuación diferencial dada en sus componentes principales. Esto implica reescribir la ecuación de manera que todas las variables y términos relacionados con y estén en un lado y los relacionados con x estén en el otro.

Paso 2: Integración de los términos

Una vez que hemos separado las variables, procedemos a integrar ambos lados de la ecuación. Este paso nos permitirá encontrar la solución general de la ecuación diferencial. Utilizamos técnicas de integración adecuadas para cada lado de la ecuación, manteniendo las constantes de integración necesarias.

Método de factor integrante

Otro enfoque para abordar esta ecuación diferencial implica el método del factor integrante. Al multiplicar la ecuación por un factor adecuado, podemos transformarla en una forma que sea más fácil de integrar, lo que nos ayudará a encontrar su solución general de manera más eficiente.

Paso 1: Identificación del factor integrante

Para utilizar este método, primero identificamos el factor integrante adecuado para la ecuación diferencial dada. Este factor se calcula a partir de los coeficientes de la ecuación y nos permite transformar la ecuación en una forma más manejable.

Paso 2: Integración de la ecuación transformada

Una vez que hemos aplicado el factor integrante y transformado la ecuación diferencial, procedemos a integrarla para encontrar su solución general. Este paso nos permite deshacernos de la derivada y obtener una expresión que representa todas las posibles soluciones de la ecuación.

Interpretación y aplicaciones

Una vez que hemos obtenido la solución general de la ecuación diferencial, es crucial analizar su significado y posibles aplicaciones. Las soluciones de ecuaciones diferenciales como la tratada en este artículo pueden ofrecer perspectivas valiosas en campos como la física, la ingeniería y la economía, proporcionando modelos matemáticos para diversos fenómenos observados en la naturaleza y la sociedad.

Análisis gráfico

Una forma de interpretar la solución de la ecuación diferencial es a través de un análisis gráfico. Graficar las soluciones en el plano xy puede proporcionar una comprensión visual de cómo se comporta la función y en relación con x, lo que puede tener implicaciones significativas en diversos contextos.

Aplicaciones en la física

En el ámbito de la física, las ecuaciones diferenciales no lineales pueden representar fenómenos complejos como el movimiento de fluidos, la propagación de ondas y el comportamiento de sistemas dinámicos. Las soluciones obtenidas a partir de estas ecuaciones pueden profundizar nuestra comprensión de dichos fenómenos y ayudarnos a formular predicciones y modelos matemáticos.

Conclusiones

En conclusión, la ecuación diferencial xy^2 dy/dx = y^3 – x^3 representa un desafío fascinante en el campo de las matemáticas y sus aplicaciones. A través de enfoques como la separación de variables y el factor integrante, podemos abordar esta ecuación de manera sistemática y alcanzar su solución general, proporcionando valiosas perspectivas sobre el comportamiento de las funciones involucradas. Las aplicaciones de estas soluciones en diversos campos destacan la importancia y relevancia de comprender y resolver ecuaciones diferenciales no lineales en el contexto actual de la investigación y la aplicación matemáticas.

“`