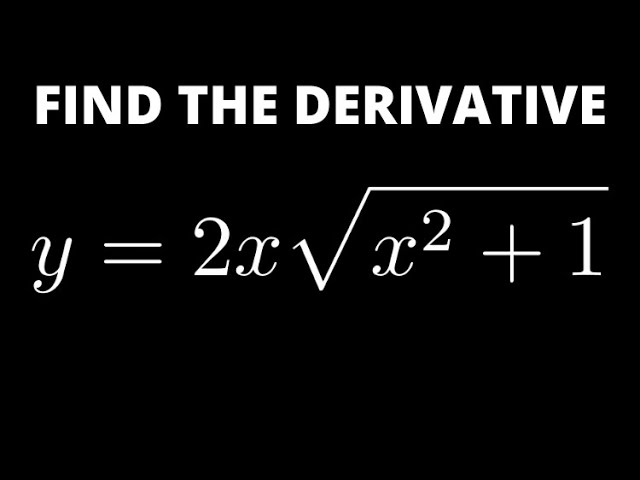Diferenciación de y con respecto a x: Introducción
La diferenciación es una parte fundamental del cálculo diferencial, y esencial en muchas disciplinas como la física y la economía. En matemáticas, la diferenciación se utiliza para calcular la tasa de cambio instantánea de una función en un determinado punto.
La diferenciación de una función y con respecto a x se representa como dy/dx. Esto significa que estamos calculando la tasa de cambio instantánea de la función y en relación a la variable x.
La diferenciación nos permite analizar cómo cambia una función a medida que modificamos el valor de la variable independiente. Por ejemplo, si tenemos una función que representa la posición de un objeto en función del tiempo, la diferenciación nos da la velocidad instantánea del objeto en cualquier momento dado.
En el cálculo diferencial, utilizamos límites para determinar la derivada de una función. La derivada representa la pendiente de la recta tangente a la función en un punto específico. La derivada también nos permite identificar los máximos y mínimos de una función, así como identificar su concavidad.
La diferenciación de y con respecto a x se puede realizar utilizando diferentes técnicas, como la regla del producto, la regla de la cadena y la regla del cociente. Estas reglas nos permiten calcular la derivada de funciones más complejas que están compuestas por varias funciones.
En resumen, la diferenciación de y con respecto a x nos permite calcular la tasa de cambio instantánea de una función en relación a la variable x. Este concepto es fundamental en el cálculo diferencial y nos brinda herramientas para analizar el comportamiento de las funciones en distintos puntos.
Cálculo de la derivada de y con respecto a x
En cálculo, la derivada representa la tasa instantánea de cambio de una función en relación a su variable independiente. Es decir, nos indica cómo varía la función en cada punto de su dominio.
Para calcular la derivada de una función y con respecto a la variable x, utilizamos la notación d/dx. Esto se lee como “la derivada de y respecto a x“.
Ahora bien, existen diferentes técnicas para calcular derivadas, dependiendo del tipo de función y los conocimientos matemáticos disponibles. Algunas de las técnicas más comunes incluyen:
Regla de potencias:
Esta regla se aplica cuando tenemos una función de la forma y = x^n, donde n es un número real. La derivada se calcula multiplicando el exponente por el coeficiente y restando 1 al exponente:
- Si n ≠ 0, entonces dy/dx = n * x^(n-1).
- Si n = 0, entonces dy/dx = 0.
Regla del producto:
Esta regla se utiliza cuando tenemos una función que es el producto de dos funciones más simples. La derivada se calcula utilizando la siguiente fórmula:
d/dx (f(x) * g(x)) = f'(x) * g(x) + f(x) * g'(x)
Regla de la cadena:
Esta regla se aplica cuando tenemos una función compuesta, es decir, una función dentro de otra función. La derivada se calcula utilizando la siguiente fórmula:
d/dx (f(g(x))) = f'(g(x)) * g'(x)
Estas son solo algunas de las técnicas utilizadas para calcular derivadas. A medida que se avanza en el estudio del cálculo, se aprenden más técnicas y se aplican en situaciones más complejas.
Es importante recordar que la derivada de una función nos proporciona información sobre la variación instantánea de la función, lo cual es de gran utilidad en áreas como la física, la ingeniería y la economía.
Aplicación de la regla del producto en la diferenciación
La regla del producto es una herramienta fundamental en la diferenciación de funciones compuestas. Esta regla nos permite encontrar la derivada de dos funciones multiplicadas entre sí.
Para aplicar la regla del producto, simplemente debemos derivar cada una de las funciones por separado y luego multiplicar los resultados obtenidos. Es decir, si tenemos dos funciones f(x) y g(x), la derivada de su producto f(x) * g(x) se obtiene de la siguiente manera:
“`html
Derivada del producto: (f(x) * g(x))’ = f'(x) * g(x) + f(x) * g'(x)
“`
Donde f'(x) es la derivada de f(x) y g'(x) es la derivada de g(x). Es importante recordar que la regla del producto sólo se aplica a funciones que son multiplicadas entre sí, no a funciones que están siendo sumadas o restadas.
Un ejemplo sencillo de aplicación de la regla del producto sería encontrar la derivada de la función f(x) = x^2 * sin(x). Aplicando la regla del producto, obtendríamos lo siguiente:
“`html
f'(x) = (x^2 * sin(x))’ = 2x * sin(x) + x^2 * cos(x)
“`
Como podemos ver, derivamos cada una de las funciones por separado y luego multiplicamos los resultados.
Es importante practicar y familiarizarse con la regla del producto para poder aplicarla correctamente en problemas más complejos de cálculo diferencial. También es conveniente recordar que existen otras reglas de derivación, como la regla de la cadena y la regla del cociente, que se utilizan en diferentes situaciones.
En resumen, la regla del producto es una herramienta útil en la diferenciación de funciones compuestas. Nos permite encontrar la derivada de dos funciones multiplicadas entre sí, derivando cada una por separado y luego multiplicando los resultados. Es importante practicar y comprender esta regla para poder utilizarla correctamente en problemas de cálculo diferencial.
Solución de la ecuación diferencial obtenida
Una ecuación diferencial es una ecuación que relaciona una función desconocida con una o más de sus derivadas. Resolver una ecuación diferencial implica encontrar la función que satisface dicha ecuación.
Para resolver una ecuación diferencial, es necesario realizar una serie de pasos que dependen del tipo de ecuación y de sus condiciones iniciales o de contorno. En general, se busca encontrar una función que cumpla con la ecuación y las condiciones dadas.
Pasos para resolver una ecuación diferencial:
- Identificar el tipo de ecuación diferencial: lineal, no lineal, homogénea, no homogénea, etc.
- Si es posible, simplificar la ecuación o escribirla en una forma más manejable.
- Encontrar la solución general de la ecuación diferencial, que es una familia de funciones que cumplen con la ecuación.
- Aplicar las condiciones iniciales o de contorno para encontrar la solución particular, que es una función con valores específicos.
Es importante destacar que no todas las ecuaciones diferenciales tienen solución analítica, es decir, una función que las resuelva de manera exacta. En muchos casos, se recurre a métodos numéricos o aproximados para obtener una solución.
Algunos de los métodos más comunes utilizados para resolver ecuaciones diferenciales son:
- Método de separación de variables
- Método de coeficientes indeterminados
- Método de variación de parámetros
- Método de solución por series
En conclusión, resolver una ecuación diferencial implica encontrar una función que satisface dicha ecuación y las condiciones dadas. Existen diferentes métodos para resolver ecuaciones diferenciales, y en algunos casos se requiere utilizar métodos numéricos o aproximados.
Interpretación geométrica de la diferenciación
La interpretación geométrica de la diferenciación se refiere a la representación visual de cómo cambia una función en un punto específico. Para entenderlo mejor, pensemos en una función como una curva en un plano cartesiano.
Derivada como pendiente de la recta tangente
La derivada de una función en un punto dado nos indica la pendiente de la recta tangente a la curva de la función en ese punto. Este concepto es fundamental para comprender la interpretación geométrica de la diferenciación.
Imaginemos que trazamos una recta tangente a la curva de la función en un punto determinado. La pendiente de esta recta es igual a la derivada de la función en ese punto.
La derivada nos da información sobre la inclinación de la curva en ese punto específico, lo cual nos ayuda a entender cómo cambia la función en esa ubicación.
Máximos, mínimos y puntos de inflexión
Otra interpretación geométrica importante de la diferenciación es la relación entre las derivadas y los máximos, mínimos y puntos de inflexión de una función.
- Si la derivada de una función es positiva en un punto, eso significa que la pendiente de la curva en ese punto es ascendente y la función tiene un mínimo local.
- Si la derivada de una función es negativa en un punto, entonces la pendiente de la curva en ese punto es descendente y la función tiene un máximo local.
- Si la derivada es igual a cero en un punto, ese puede ser un máximo, un mínimo o un punto de inflexión, y debemos realizar más análisis para determinar cuál es el caso.
Estos son solo algunos ejemplos de cómo podemos interpretar geométricamente la diferenciación en el contexto de las funciones. La geometría nos permite visualizar y comprender mejor el comportamiento de las funciones en diferentes puntos y entender cómo cambian en relación con sus derivadas.