La distribución de probabilidad normal es un concepto fundamental en estadística y probabilidad. Se utiliza para modelar una amplia variedad de fenómenos naturales y se encuentra ampliamente en la teoría y la práctica de diferentes disciplinas. En este artículo, exploraremos en profundidad la distribución de probabilidad normal, sus características y su importancia en diversos contextos.
Definición y Fundamentos
La distribución de probabilidad normal, también conocida como distribución gaussiana, es una distribución de probabilidad continua que está completamente determinada por su media y su desviación estándar. Se caracteriza por tener una forma de campana simétrica en torno a su media, lo que la hace particularmente útil para modelar fenómenos en los que la media es el valor más probable y los valores extremos son menos probables.
Función de densidad de probabilidad
La distribución normal se describe mediante su función de densidad de probabilidad, que es una función matemática que representa la forma de la curva de campana. Esta función está determinada por la fórmula matemática específica que define la distribución normal en términos de su media (μ) y desviación estándar (σ).
Características Principales
Existen varias características fundamentales que definen la distribución de probabilidad normal y la hacen especialmente relevante en distintos ámbitos:
Simetria y forma de campana
Una de las características más distintivas de la distribución normal es su simetría en torno a la media, lo que se traduce en una forma de campana en su gráfica de densidad de probabilidad. Esta simetría implica que la mitad de la distribución se encuentra a cada lado de la media, lo que la hace útil para modelar fenómenos donde los valores extremos son menos probables que los valores cercanos a la media.
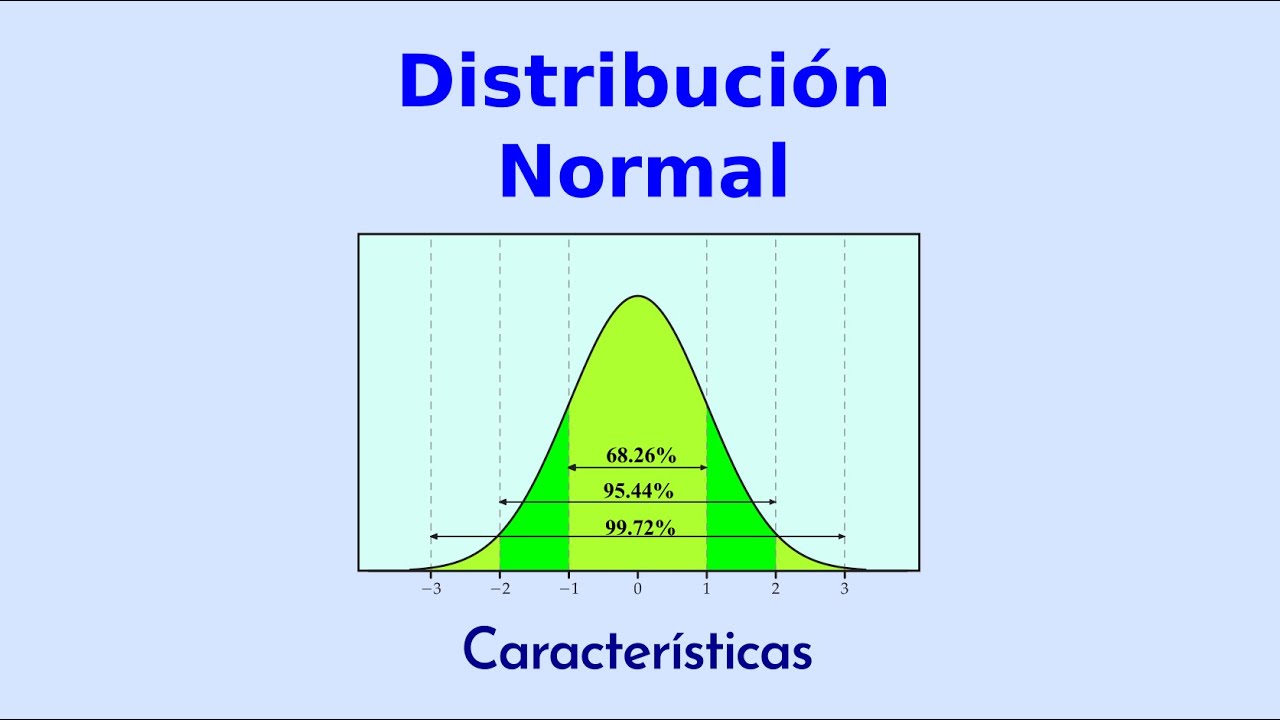
Regla 68-95-99.7
La distribución normal sigue la conocida regla empírica del 68-95-99.7, que establece que aproximadamente el 68% de los datos se encuentran dentro de una desviación estándar de la media, alrededor del 95% dentro de dos desviaciones estándar, y casi la totalidad (99.7%) dentro de tres desviaciones estándar. Esta regla es de gran utilidad para comprender la dispersión de los datos en una distribución normal.
Aplicaciones y Significado
La distribución de probabilidad normal tiene una amplia gama de aplicaciones en la práctica y la investigación en diversas disciplinas. Algunas de las aplicaciones más destacadas incluyen:
Modelado de procesos naturales
En la física, biología, economía y otras disciplinas, la distribución normal se utiliza para modelar fenómenos naturales como la distribución de tamaños de moléculas, la altura de una población, o la distribución de ingresos. Su simetría y propiedades estadísticas la hacen especialmente idónea para estas aplicaciones.
Estadística inferencial
En estadística, la distribución normal desempeña un papel fundamental en la inferencia estadística y en la construcción de intervalos de confianza. La asunción de normalidad en muchos métodos estadísticos permite tomar decisiones basadas en la teoría de la probabilidad y estimar parámetros de la población de interés.
Propiedades Matemáticas
La distribución de probabilidad normal también posee varias propiedades matemáticas que la hacen única y relevante en la teoría de la probabilidad y la estadística:
Transformaciones lineales
Una de las propiedades más importantes de la distribución normal es que cualquier combinación lineal de variables aleatorias independientes y normalmente distribuidas también sigue una distribución normal. Esta propiedad es clave en muchas aplicaciones, como en la corrección de errores de medición en instrumentos científicos.
Distribución límite
Otra propiedad relevante es que la distribución normal surge como la distribución límite de la suma de un gran número de variables aleatorias independientes e idénticamente distribuidas. Este resultado, conocido como el teorema del límite central, es fundamental en estadística y tiene aplicaciones en la inferencia estadística.
En resumen, la distribución de probabilidad normal es un concepto central en la teoría de la probabilidad y la estadística, con una amplia gama de aplicaciones en distintos campos. Sus características únicas, propiedades matemáticas y relevancia en la modelización de fenómenos naturales la hacen indispensable en la comprensión y el análisis de datos. Comprender a fondo la distribución de probabilidad normal es esencial para cualquier persona interesada en la ciencia de datos, la investigación científica y la toma de decisiones fundamentadas en datos.