La Teoría de Conjuntos es un campo fundamental en las Matemáticas que juega un papel crucial en el desarrollo de esta disciplina. Comprender los fundamentos de la Teoría de Conjuntos es esencial para tener una base sólida en Matemáticas y para poder abordar problemas más avanzados en áreas como la Probabilidad, la Lógica y la Teoría de Números, entre otras. En este artículo, exploraremos en detalle los conceptos clave de la Teoría de Conjuntos, proporcionando claves para dominar este tema y mejorar la comprensión de las Matemáticas en general.
Fundamentos de la Teoría de Conjuntos
Definición y elementos básicos
En la Teoría de Conjuntos, un conjunto es una colección bien definida de elementos distintos. Un conjunto se representa usualmente mediante llaves {} y se escriben los elementos separados por comas. Por ejemplo, el conjunto de los números naturales se representa como {1, 2, 3, …}.
Un conjunto puede contener tanto elementos individuales como elementos abstractos. Por ejemplo, el conjunto de letras del alfabeto se representa como {a, b, c, … , z}. En este caso, los elementos son letras individuales. Por otro lado, el conjunto de todos los números pares puede representarse como {2, 4, 6, …}, donde los elementos son números abstractos que tienen en común la propiedad de ser pares.
Es importante destacar que un conjunto no puede tener elementos repetidos, es decir, todos los elementos deben ser distintos entre sí.
Existen conjuntos finitos e infinitos. Los conjuntos finitos tienen un número finito de elementos, como por ejemplo el conjunto de los meses del año. Por otro lado, los conjuntos infinitos tienen un número infinito de elementos, como el conjunto de números naturales.
Relaciones entre conjuntos
En la Teoría de Conjuntos, existen varias relaciones importantes entre conjuntos que permiten comparar, combinar y manipular conjuntos de diferentes maneras.
Un conjunto A se considera subconjunto de otro conjunto B si todos los elementos de A también están en B. Se denota como A ⊆ B. Un conjunto que contiene todos los elementos de otro conjunto se conoce como superconjunto. Se denota como B ⊇ A.
El conjunto vacío, representado como ∅, es un conjunto que no contiene ningún elemento. Por otro lado, el conjunto universal U es un conjunto que contiene a todos los elementos en consideración.
Las operaciones fundamentales con conjuntos son la intersección, la unión y la diferencia.
La intersección de dos conjuntos A y B, denotada como A ∩ B, es un conjunto que contiene todos los elementos que están en A y también están en B. Por ejemplo, si A = {1, 2, 3} y B = {2, 3, 4}, entonces A ∩ B = {2, 3}.
La unión de dos conjuntos A y B, denotada como A ∪ B, es un conjunto que contiene todos los elementos que están en A, en B, o en ambos conjuntos. Por ejemplo, si A = {1, 2, 3} y B = {2, 3, 4}, entonces A ∪ B = {1, 2, 3, 4}.
La diferencia entre dos conjuntos A y B, denotada como A – B, es un conjunto que contiene todos los elementos que están en A pero no están en B. Por ejemplo, si A = {1, 2, 3} y B = {2, 3, 4}, entonces A – B = {1}.
Diagramas de Venn
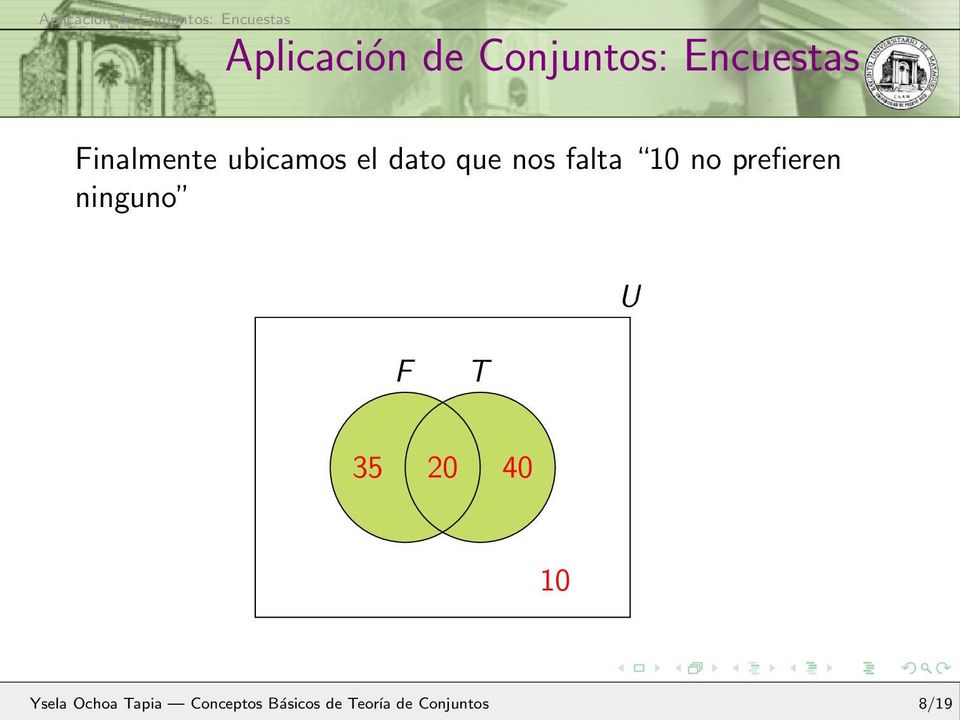
Los diagramas de Venn son herramientas gráficas que permiten representar las relaciones entre conjuntos. Estos diagramas consisten en círculos superpuestos, cada uno representando un conjunto, y áreas sombreadas que indican qué elementos están en cada conjunto y cómo se relacionan entre sí.
Los diagramas de Venn son especialmente útiles para resolver problemas de conjuntos y visualizar las diferentes operaciones entre ellos. Por ejemplo, si se tienen tres conjuntos A, B y C, se pueden crear diagramas de Venn que muestren la intersección, la unión y la diferencia entre estos conjuntos.
Por ejemplo, si se tienen A = {1, 2, 3}, B = {2, 3, 4} y C = {3, 4, 5}, se puede dibujar un diagrama de Venn con tres círculos superpuestos. El área donde se superponen los tres círculos representa la intersección de los tres conjuntos. Las áreas donde se superponen dos círculos representan las intersecciones entre dos conjuntos, y las áreas individuales de cada círculo representan los conjuntos individuales.
Propiedades y operaciones avanzadas
Conjuntos disjuntos y conjuntos complemento
En la Teoría de Conjuntos, se dice que dos conjuntos son disjuntos si no tienen elementos en común, es decir, su intersección es el conjunto vacío. Por ejemplo, si A = {1, 2, 3} y B = {4, 5, 6}, entonces A y B son conjuntos disjuntos.
Por otro lado, el complemento de un conjunto A con respecto a un conjunto universal U, denotado como A’, es un conjunto que contiene todos los elementos en U que no están en A. Por ejemplo, si U es el conjunto de todos los números enteros y A es el conjunto de números pares, entonces A’ es el conjunto de números impares.
Leyes de De Morgan
Las leyes de De Morgan son una serie de identidades que relacionan las operaciones de complemento, intersección y unión en conjuntos.
La primera ley de De Morgan establece que el complemento de la unión de dos conjuntos es igual a la intersección de sus complementos. Matemáticamente, se expresa de la siguiente manera:
(A ∪ B)’ = A’ ∩ B’
La segunda ley de De Morgan establece que el complemento de la intersección de dos conjuntos es igual a la unión de sus complementos. Matemáticamente, se expresa de la siguiente manera:
(A ∩ B)’ = A’ ∪ B’
Estas leyes son útiles para simplificar expresiones booleanas y para demostrar propiedades en la Teoría de Conjuntos.
Producto cartesiano
El producto cartesiano es una operación que permite combinar elementos de diferentes conjuntos para formar parejas ordenadas. El producto cartesiano entre dos conjuntos A y B, denotado como A x B, es un conjunto que contiene todas las parejas ordenadas (a, b), donde a pertenece a A y b pertenece a B.
El producto cartesiano es especialmente útil para representar relaciones entre conjuntos. Por ejemplo, si se tienen los conjuntos A = {1, 2} y B = {a, b, c}, el producto cartesiano A x B contiene las siguientes parejas ordenadas:
A x B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)}
Cardinalidad de conjuntos
En la Teoría de Conjuntos, la cardinalidad de un conjunto es el número de elementos que contiene. Se denota como |A|, donde A es el conjunto en cuestión.
La cardinalidad de un conjunto finito se calcula simplemente contando el número de elementos en el conjunto. Por ejemplo, si A = {1, 2, 3}, entonces |A| = 3.
En el caso de conjuntos infinitos, la cardinalidad se compara utilizando conceptos como igualdad de cardinalidades, cardinalidad más pequeña y cardinalidad más grande. Por ejemplo, se dice que el conjunto de números naturales tiene una cardinalidad más pequeña que el conjunto de números reales, ya que hay una correspondencia uno a uno entre los números naturales y los números enteros positivos.
Aplicaciones de la Teoría de Conjuntos
Probabilidad y teoría de conjuntos
La Teoría de Conjuntos es fundamental en el campo de la Probabilidad, ya que permite calcular la probabilidad de eventos utilizando conjuntos. La probabilidad de un evento se define como el número de casos favorables dividido por el número total de casos posibles.
Se utilizan conjuntos para representar el espacio muestral, que es el conjunto de todos los posibles resultados de un experimento aleatorio. Los eventos se representan mediante subconjuntos del espacio muestral. La probabilidad de un evento se calcula como la cardinalidad del evento dividida por la cardinalidad del espacio muestral.
Por ejemplo, si se tiene un experimento en el que se lanza un dado de seis caras, el espacio muestral contiene los resultados posibles: {1, 2, 3, 4, 5, 6}. Si se desea calcular la probabilidad de obtener un número par, el evento se representa como {2, 4, 6}. La probabilidad de este evento es 3/6 = 1/2.
Lógica y teoría de conjuntos
La Teoría de Conjuntos también tiene aplicaciones en el campo de la Lógica, especialmente en la lógica proposicional y la lógica de predicados.
En la lógica proposicional, las variables proposicionales y los conectores lógicos pueden representarse mediante conjuntos. Por ejemplo, si se tiene la proposición «Si llueve, entonces me quedo en casa», se pueden representar las variables propisicionales «llueve» y «me quedo en casa» como conjuntos. El conjunto que representa «llueve» contiene todos los posibles valores verdadero o falso que puede tomar esta variable.
En la lógica de predicados, los conjuntos se utilizan para representar conjuntos de objetos y relaciones entre ellos. Por ejemplo, si se desea representar la proposición «Para todo x, si x es un número par, entonces x es divisible por 2», se puede utilizar un conjunto que representa el conjunto de todos los números enteros y operaciones lógicas para expresar la relación.
La Teoría de Conjuntos es un campo fundamental en Matemáticas que proporciona una base sólida para abordar problemas más avanzados en diferentes áreas. En este artículo, hemos explorado en detalle los conceptos clave de la Teoría de Conjuntos, desde los fundamentos de los conjuntos hasta operaciones avanzadas como las leyes de De Morgan y el producto cartesiano. También hemos discutido las aplicaciones de la Teoría de Conjuntos en la Probabilidad y la Lógica. Dominar la Teoría de Conjuntos es esencial para tener una comprensión sólida de las Matemáticas y poder resolver problemas con solidez.
Si deseas mejorar tu comprensión de la Teoría de Conjuntos, se recomienda practicar con ejercicios y problemas variados, así como buscar cursos y recursos adicionales que profundicen en este tema. La Teoría de Conjuntos es un área amplia y fascinante que te abrirá puertas en muchas otras áreas de las Matemáticas. ¡No te detengas aquí, sigue aprendiendo y expandiendo tus conocimientos!