Una circunferencia con centro en el origen y radio de 15 es una forma geométrica fundamental que tiene muchas aplicaciones en matemáticas, física y otras disciplinas. En este artículo, exploraremos en detalle cómo encontrar la ecuación de esta circunferencia y comprender su significado geométrico.
Además, discutiremos cómo esta ecuación se relaciona con otros conceptos matemáticos y cómo se puede emplear para resolver problemas del mundo real.
Hallar la ecuación de la circunferencia
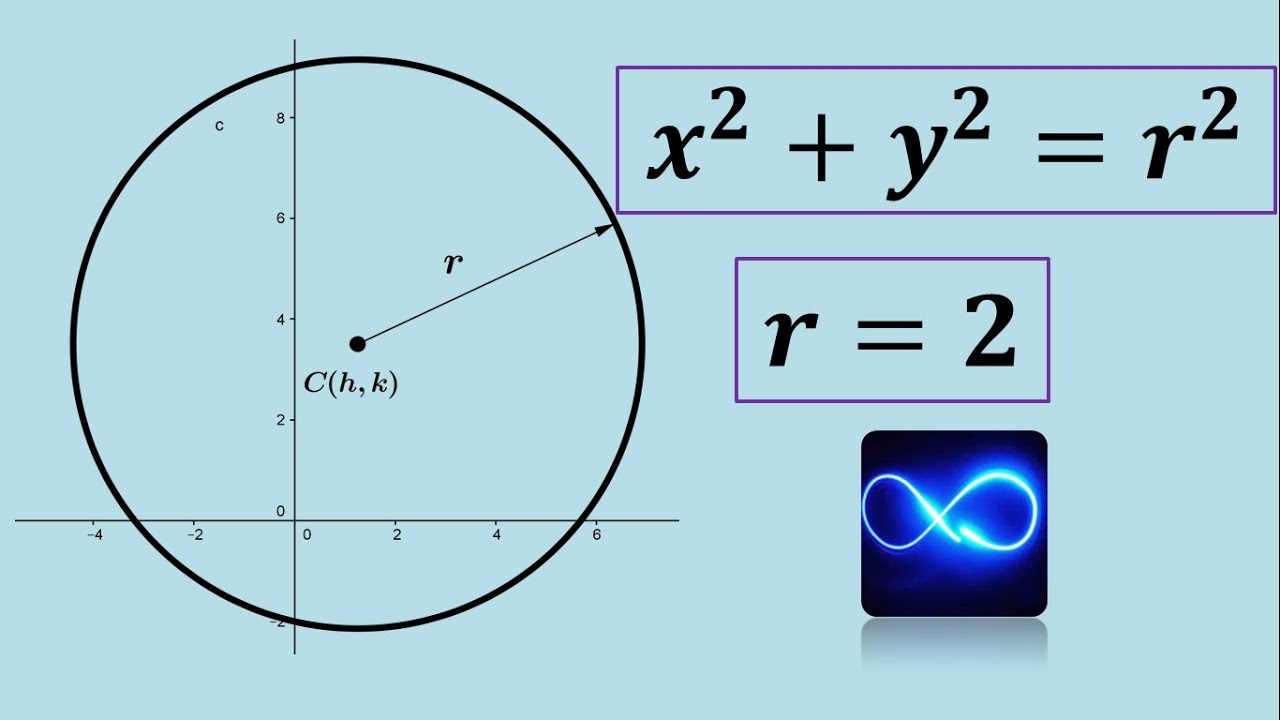
El primer paso para encontrar la ecuación de la circunferencia con centro en el origen y radio de 15 es comprender la forma estándar de la ecuación de una circunferencia. En coordenadas cartesianas, la ecuación de una circunferencia con centro en (h, k) y radio r está dada por la fórmula:
(x – h)² + (y – k)² = r²
Para el caso de una circunferencia con centro en el origen (0, 0), la ecuación se simplifica a:
x² + y² = r²
Interpretación geométrica
La ecuación anterior representa todas las posibles combinaciones de valores de x e y que satisfacen la restricción imposta por la circunferencia con centro en el origen y radio de 15. Geométricamente, esto significa que todos los puntos (x, y) que satisfacen la ecuación están ubicados a una distancia de 15 unidades del origen.
Esta representación geométrica nos permite visualizar la forma de la circunferencia y comprender cómo se relaciona con otras formas y objetos en el plano cartesiano.
Entendiendo las coordenadas
Un aspecto interesante de la ecuación de la circunferencia con centro en el origen es que nos permite comprender cómo los valores de x e y interactúan para ubicar puntos en relación con la circunferencia. Por ejemplo, si queremos encontrar las coordenadas de un punto en la circunferencia con un ángulo específico θ con respecto al eje x positivo, podemos usar las funciones trigonométricas seno y coseno para calcular las coordenadas.
Si el radio de la circunferencia es 15, entonces las coordenadas de un punto en la circunferencia son (15*cos(θ), 15*sen(θ)), donde θ es el ángulo medido en radianes.
Relación con el círculo unitario
La circunferencia con centro en el origen y radio de 15 se relaciona de manera interesante con el concepto de círculo unitario en trigonometría. El círculo unitario es una circunferencia con radio 1 y centro en el origen, que juega un papel crucial en el estudio de las funciones trigonométricas.
Al comparar la circunferencia con centro en el origen y radio de 15 con el círculo unitario, podemos observar cómo las funciones trigonométricas están relacionadas con la geometría de la circunferencia y cómo se pueden usar para resolver problemas geométricos y analíticos.
Aplicaciones en el mundo real
Además de su importancia teórica, la ecuación de la circunferencia con centro en el origen y radio de 15 tiene numerosas aplicaciones en el mundo real. Por ejemplo, en el diseño de ruedas o engranajes, esta ecuación puede utilizarse para modelar la forma y el tamaño de las circunferencias necesarias para girar un mecanismo dado.
Del mismo modo, en astronomía, la órbita de un planeta alrededor del sol puede modelarse mediante una ecuación de circunferencia, lo que permite a los científicos comprender y predecir el movimiento de los cuerpos celestes con gran precisión.
Generalización a otras dimensiones
Hasta ahora, hemos estado discutiendo la ecuación de la circunferencia con centro en el origen y radio de 15 en el contexto del plano cartesiano bidimensional. Sin embargo, es importante destacar que estos conceptos se pueden generalizar a espacios de mayor dimensión.
En un espacio tridimensional, por ejemplo, la ecuación de una esfera con centro en el origen y radio de 15 tendría la forma x² + y² + z² = r², donde (x, y, z) son las coordenadas tridimensionales de un punto en el espacio.
Conclusiones
En resumen, la ecuación de la circunferencia con centro en el origen y radio de 15 es un concepto fundamental en matemáticas y tiene una amplia gama de aplicaciones en varios campos. Comprender cómo encontrar esta ecuación, su interpretación geométrica y sus conexiones con otros conceptos matemáticos es crucial para desarrollar habilidades analíticas y geométricas sólidas.
Además, la capacidad de generalizar estos conceptos a espacios de mayor dimensión amplía aún más su relevancia y utilidad en el estudio y la resolución de problemas del mundo real.