¿Qué es una ecuación de la recta?
Una ecuación de la recta es una fórmula matemática que describe una línea recta en un plano cartesiano. Dicha ecuación establece la relación entre las coordenadas x e y de los puntos que pertenecen a la recta.
La forma general de una ecuación de la recta es y = mx + b, donde m es la pendiente de la recta y b es el término independiente, que representa el punto de intersección de la recta con el eje y.
La pendiente de una recta indica la inclinación o la dirección de la misma. Si la pendiente es positiva, la recta tiene una inclinación ascendente de izquierda a derecha; si es negativa, la inclinación es descendente de izquierda a derecha. Una pendiente de cero indica una línea horizontal, mientras que una pendiente infinita representa una línea vertical.
El término independiente b determina la posición vertical de la recta. Si b es igual a cero, la recta atraviesa el origen de coordenadas (0,0); si b es mayor a cero, la recta se cruza con el eje y por encima del origen; y si b es menor a cero, la recta se cruza con el eje y por debajo del origen.
En resumen, una ecuación de la recta nos permite determinar la posición y la inclinación de una línea recta en un plano cartesiano. Mediante la pendiente y el término independiente, podemos trazar la recta y calcular las coordenadas de cualquier punto que pertenezca a ella.
Fórmula de la ecuación de la recta
La fórmula de la ecuación de la recta es una herramienta fundamental en el estudio de la geometría analítica. Permite representar una línea recta en un sistema de coordenadas cartesianas.
La fórmula general de la ecuación de la recta es: y = mx + b, donde:
- y representa la coordenada en el eje y
- x representa la coordenada en el eje x
- m es la pendiente de la recta
- b es el punto de intersección con el eje y, también conocido como la ordenada al origen
La pendiente de la recta, representada por m, indica el grado de inclinación de la línea. Se calcula dividiendo el cambio en la coordenada y por el cambio en la coordenada x entre dos puntos en la recta.
El punto de intersección con el eje y, representado por b, se encuentra donde la recta cruza dicho eje. Para encontrar su valor, es necesario conocer al menos otro punto en la recta.
Conociendo la pendiente y el punto de intersección con el eje y, podemos graficar la recta en un plano cartesiano.
Además de la fórmula general, existen otras formas de escribir la ecuación de la recta, como la forma pendiente-intercepto y la forma punto-pendiente, que resultan útiles en diferentes situaciones.
En resumen, la fórmula de la ecuación de la recta, y = mx + b, es una herramienta esencial para representar y entender líneas rectas en un sistema de coordenadas cartesianas.
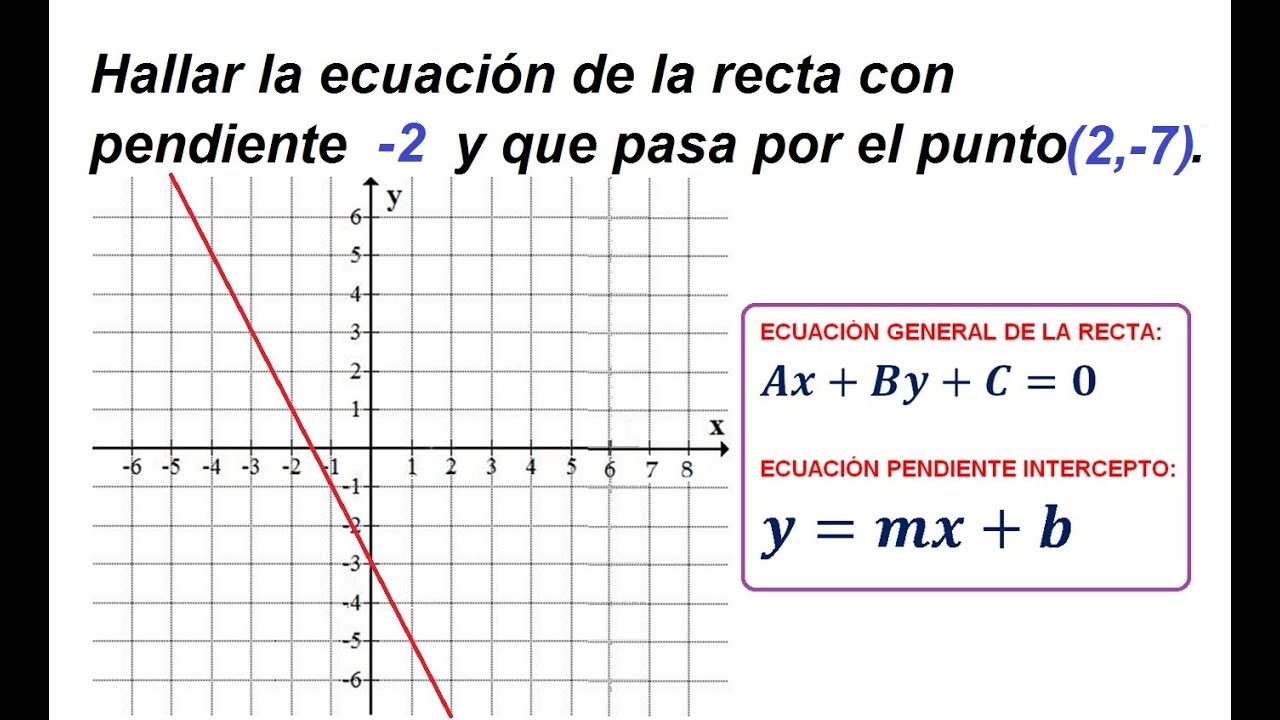
Encontrar la ecuación de la recta que pasa por un punto dado con una pendiente dada
Para encontrar la ecuación de una recta que pasa por un punto dado con una pendiente dada, podemos utilizar la fórmula de la pendiente-intersección, también conocida como la forma punto-pendiente.
La fórmula de la pendiente-intersección es y = mx + b, donde m es la pendiente de la recta y b es la coordenada y donde la recta intersecta el eje y.
Podemos utilizar la siguiente lista de pasos para encontrar la ecuación de la recta:
- Identificar el valor de la pendiente m y las coordenadas (x, y) del punto dado.
- Sustituir la pendiente m en la fórmula de la pendiente-intersección.
- Sustituir las coordenadas (x, y) del punto dado en la ecuación obtenida en el paso anterior.
- Resolver la ecuación para encontrar el valor de b.
- Escribir la ecuación de la recta utilizando el valor de m y el valor de b obtenidos en los pasos anteriores.
Así que, para encontrar la ecuación de la recta que pasa por un punto dado con una pendiente dada, simplemente sigue estos pasos y sustituye los valores correspondientes en la fórmula de la pendiente-intersección.
Verificar la solución
En cualquier proyecto o situación, es crucial verificar la solución propuesta antes de tomar decisiones o implementar cambios. La verificación es un proceso de evaluación que tiene como objetivo asegurarse de que la solución propuesta cumple con los requisitos y soluciona el problema planteado.
Para llevar a cabo la verificación de la solución, es importante prestar atención a las frases más importantes del texto. Estas frases suelen resumir los puntos clave y brindar una visión general de la solución propuesta. Para resaltar estas frases, se pueden utilizar las etiquetas HTML o , que aplican formato de negrita al texto.
Algunos pasos a seguir para verificar la solución son:
- Analizar los requisitos: Comprender a fondo los requisitos del proyecto o problema planteado es fundamental para verificar la solución propuesta. Esto implica revisar los documentos, especificaciones o cualquier información relevante.
- Comparar con la solución propuesta: Evaluar si la solución propuesta se alinea con los requisitos analizados. Es importante prestar atención a los detalles y asegurarse de que cada aspecto clave esté abordado.
- Realizar pruebas: Probar la solución propuesta en un entorno controlado es una manera efectiva de verificar su funcionamiento. Las pruebas pueden incluir escenarios típicos, situaciones extremas y cualquier caso especial identificado previamente.
- Recopilar feedback: Obtener opiniones y retroalimentación de personas involucradas en el proyecto o de usuarios finales es una forma valiosa de verificar la solución propuesta. Esto ayuda a identificar posibles mejoras o ajustes necesarios.
- Tomar decisiones: Basándose en los resultados de la verificación y el feedback recibido, es necesario tomar decisiones informadas sobre la solución propuesta. Esto puede implicar ajustes, mejoras o incluso la elección de una solución alternativa.
La verificación de la solución es un paso esencial antes de su implementación o ejecución. Ayuda a evitar errores y asegura que la solución cumple con los requisitos establecidos. Siguiendo estos pasos y prestando atención a las frases más importantes, se puede realizar una verificación eficiente y efectiva.