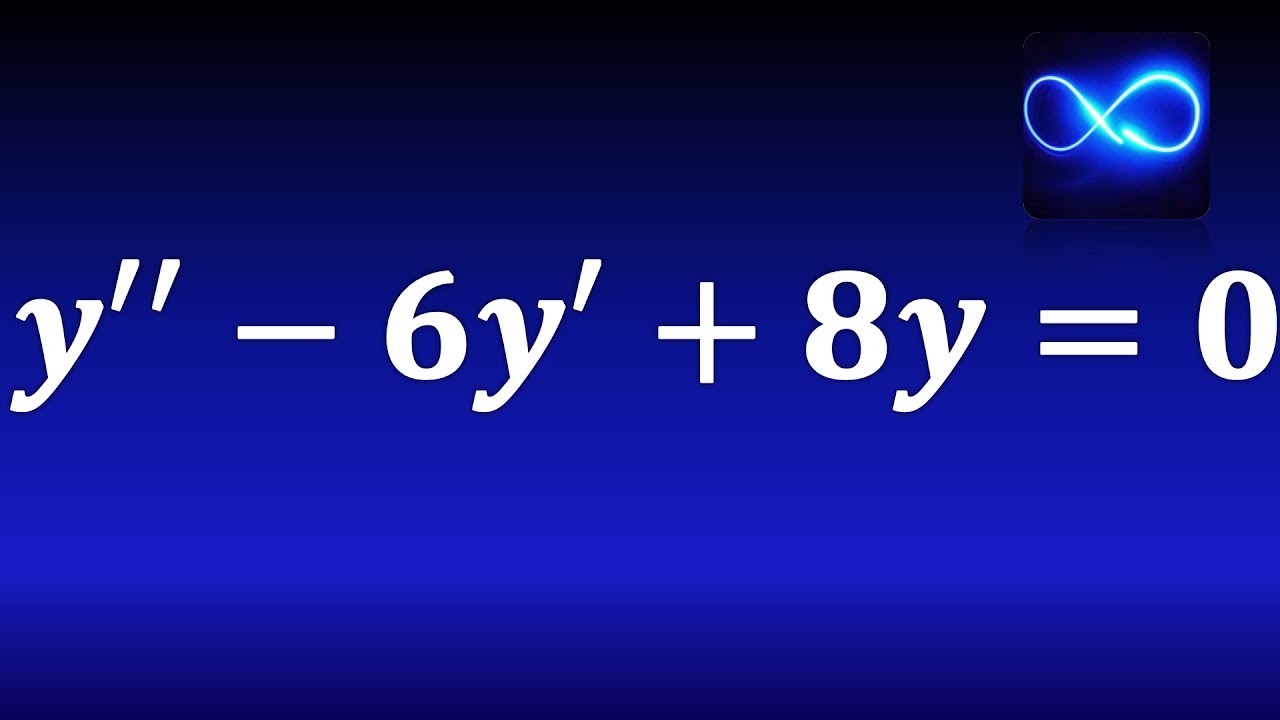Una ecuación diferencial de segundo orden con coeficientes constantes es un tipo particular de ecuación diferencial que aparece con frecuencia en la física y la ingeniería. Este tipo de ecuación es de suma importancia debido a su amplio rango de aplicaciones, que van desde problemas de movimiento armónico simple hasta circuitos eléctricos y fenómenos de vibración. En este artículo, exploraremos en detalle cómo resolver este tipo de ecuaciones paso a paso, brindando una comprensión profunda y clara de los conceptos involucrados.
La forma general de la ecuación diferencial
Antes de sumergirnos en la resolución de la ecuación diferencial de segundo orden con coeficientes constantes, es crucial comprender su forma general. Esta ecuación se puede expresar de la siguiente manera:
dy/dx + ay» + by’ + cy = 0
Donde y es la función desconocida dependiente de x, y’ y y» representan la primera y segunda derivada de y con respecto a x, respectivamente, y a, b y c son coeficientes constantes.
Resolviendo la ecuación diferencial de segundo orden con coeficientes constantes: Paso a paso
Ahora que estamos familiarizados con la forma general de la ecuación diferencial de segundo orden, procederemos a resolverla paso a paso. Este proceso implicará técnicas como encontrar la solución homogénea, la solución particular y la solución general, así como la aplicación de condiciones iniciales si corresponde.
Encontrando la solución homogénea
La primera etapa en la resolución de la ecuación diferencial de segundo orden es encontrar la solución homogénea. Esto implica resolver la ecuación característica asociada, que se obtiene al reemplazar y» por m^2, y’ por m y y por 1 en la ecuación original. La ecuación característica toma la forma:
m^2 + bm + c = 0
Donde m es una variable. Dependiendo de las raíces de esta ecuación característica, la solución homogénea tomará una de las siguientes formas:
Caso 1: Raíces reales distintas
Si las raíces de la ecuación característica son reales y distintas, la solución homogénea estará dada por:
y_h = c1e^(m1x) + c2e^(m2x)
Donde c1 y c2 son constantes que se determinan a partir de condiciones iniciales si estas se proporcionan.
Caso 2: Raíces reales repetidas
En el caso de que las raíces de la ecuación característica sean reales pero repetidas, la solución homogénea será:
y_h = (c1 + c2x)e^(mx)
Donde c1 y c2 son constantes.
Caso 3: Raíces complejas
Si las raíces de la ecuación característica son complejas, por ejemplo, m = α ± βi, la solución homogénea se expresa como:
y_h = e^(αx)(c1cos(βx) + c2sin(βx))
Donde c1 y c2 son constantes.
Encontrando la solución particular
Una vez que se ha encontrado la solución homogénea, el siguiente paso es buscar una solución particular de la ecuación diferencial original. La forma de esta solución particular dependerá del lado derecho de la ecuación diferencial, es decir, de la función f(x) en dy/dx + ay» + by’ + cy = f(x). Para encontrar una solución particular, se pueden utilizar métodos como el método de los coeficientes indeterminados o el método de la variación de parámetros, dependiendo de f(x).
Formando la solución general
Una vez que se ha obtenido la solución homogénea y la solución particular, la solución general de la ecuación diferencial se forma sumando la solución homogénea y la solución particular. Esto proporciona la forma general de la solución y se pueden determinar las constantes involucradas usando las condiciones iniciales si estas se proporcionan.
Aplicando condiciones iniciales
En muchos problemas físicos o de ingeniería, se proporcionarán condiciones iniciales que permiten determinar los valores de las constantes presentes en la solución general. Estas condiciones iniciales suelen tomar la forma de valores de y, y’ o y» en ciertos puntos específicos del dominio, y se utilizan para resolver las constantes desconocidas y obtener una solución específica para el problema en cuestión.
A lo largo de este artículo, hemos desglosado el proceso de resolución de una ecuación diferencial de segundo orden con coeficientes constantes, desde la forma general de la ecuación hasta la obtención de la solución general e la aplicación de condiciones iniciales. Este tipo de ecuación es fundamental en numerosos contextos y dominios de la ciencia y la ingeniería, y comprender su resolución paso a paso es esencial para abordar una variedad de problemas prácticos de manera efectiva.