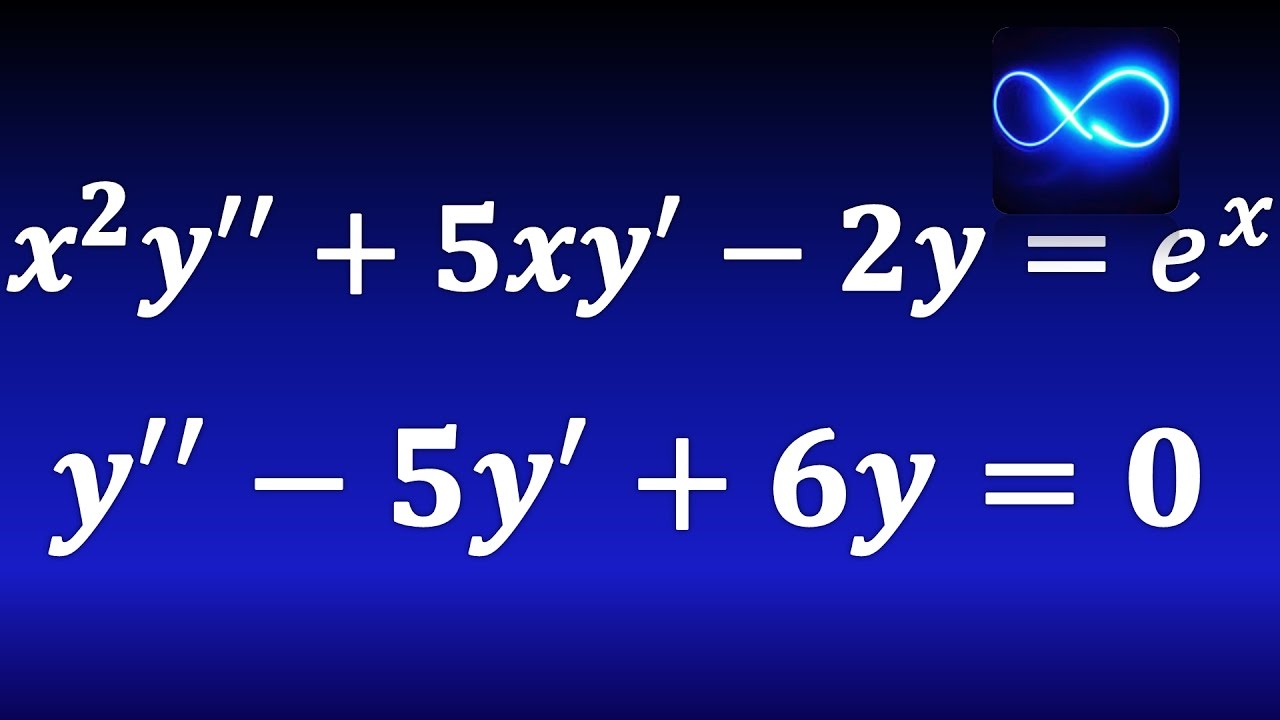¿Qué es una ecuación diferencial de segundo orden?
Una ecuación diferencial de segundo orden es una ecuación que involucra una función desconocida, su derivada primera y su derivada segunda. Estas ecuaciones son comúnmente utilizadas en diferentes disciplinas como la física, la ingeniería, la economía y la biología para describir fenómenos que cambian con respecto a dos variables independientes.
Las ecuaciones diferenciales de segundo orden son más complejas que las ecuaciones diferenciales de primer orden, ya que contienen información adicional sobre la función desconocida y su comportamiento. Estas ecuaciones pueden ser clasificadas en tres categorías principales: lineales, no lineales y lineales pero no homogéneas.
En una ecuación diferencial de segundo orden lineal, la función desconocida y sus derivadas aparecen de manera lineal. Este tipo de ecuaciones se pueden resolver utilizando métodos como la combinación de soluciones particulares y homogéneas.
En cambio, una ecuación diferencial de segundo orden no lineal incluye términos no lineales de la función desconocida o sus derivadas. La solución de este tipo de ecuaciones es más compleja y generalmente requiere técnicas numéricas o aproximaciones.
Por último, una ecuación diferencial de segundo orden lineal pero no homogénea contiene términos que no se cancelan en la solución homogénea. Su solución general se obtiene sumando la solución específica de la ecuación no homogénea con la solución general de la ecuación homogénea.
En resumen, una ecuación diferencial de segundo orden es una herramienta matemática utilizada para modelar fenómenos que involucran dos variables independientes y su solución depende de la naturaleza de la ecuación. Estas ecuaciones son ampliamente utilizadas en diversas áreas de la ciencia y la ingeniería para describir y predecir el comportamiento de sistemas dinámicos.
Características de las ecuaciones diferenciales de segundo orden
Las ecuaciones diferenciales de segundo orden son aquellas en las que la incógnita depende de su segunda derivada.
Estas ecuaciones suelen presentar diversas características que las distinguen de las de orden inferior. Algunas de estas características son:
- Mayor complejidad: Al involucrar la segunda derivada, las ecuaciones diferenciales de segundo orden son más complejas que las de primer orden.
- Mayor expresividad: La presencia de la segunda derivada proporciona mayor información sobre la función incógnita, lo que permite modelar fenómenos más diversos y detallados.
- Solución general: A diferencia de las ecuaciones de primer orden, las ecuaciones diferenciales de segundo orden suelen tener una solución general que depende de dos constantes arbitrarias.
- Tres clases de soluciones: Dependiendo de las raíces del polinomio característico asociado a la ecuación, estas pueden presentar soluciones reales distintas, soluciones complejas conjugadas o raíces repetidas.
En resumen, las ecuaciones diferenciales de segundo orden son más complejas que las de primer orden, pero también más expresivas. Poseen una solución general que depende de dos constantes arbitrarias y pueden presentar diferentes tipos de soluciones dependiendo de las raíces del polinomio característico.
Métodos de resolución
En la resolución de problemas, existen diferentes métodos que se pueden utilizar para encontrar soluciones eficientes y efectivas. A continuación, se presentan algunos de los métodos más comunes utilizados:
1. Método de ensayo y error:
Este método implica probar diferentes posibilidades hasta encontrar la solución adecuada. A medida que se realizan más intentos, se van descartando las opciones que no funcionan, lo que permite acercarse cada vez más a la solución. Es un enfoque simple, pero puede ser tedioso y consumir mucho tiempo.
2. Método de división y conquista:
Este método consiste en dividir un problema en subproblemas más pequeños y más fáciles de resolver. Cada subproblema se aborda de manera individual y luego se combinan las soluciones para resolver el problema original. Es útil cuando el problema puede descomponerse en partes más simples y cuando se dispone de los recursos necesarios para abordar cada subproblema.
3. Método de prueba y evaluación:
Este método implica probar diferentes soluciones y evaluar su efectividad. Se pueden probar diferentes enfoques y técnicas para encontrar la mejor solución posible. A medida que se realizan pruebas, se evalúan los resultados y se ajusta el enfoque en consecuencia.
4. Método heurístico:
Este método se basa en la experiencia y el conocimiento previo para encontrar soluciones. Se utilizan reglas generales o estrategias aprendidas para resolver el problema. Aunque puede no garantizar una solución óptima, puede ser útil cuando se dispone de poco tiempo o información limitada.
5. Método de programación lineal:
Este método se utiliza en problemas que implican la maximización o minimización de una función lineal sujeta a restricciones. Se utiliza un conjunto de ecuaciones y desigualdades para representar el problema y se busca la solución que optimice la función objetivo.
Estos son solo algunos ejemplos de métodos de resolución utilizados en diferentes disciplinas y situaciones. La elección del método adecuado depende del problema específico y los recursos disponibles.
Aplicaciones de las ecuaciones diferenciales de segundo orden con términos exponenciales y constantes
Las ecuaciones diferenciales de segundo orden con términos exponenciales y constantes son fundamentales en muchas áreas de la ciencia y la ingeniería. Estas ecuaciones permiten modelar una amplia gama de fenómenos físicos y naturales que involucran cambios en el tiempo.
1. Mecánica clásica
En la mecánica clásica, las ecuaciones diferenciales de segundo orden con términos exponenciales y constantes se utilizan para describir el movimiento de partículas y sistemas físicos. Por ejemplo, la ecuación del oscilador armónico es una ecuación diferencial de segundo orden que muestra cómo se mueve un objeto bajo la influencia de una fuerza restauradora proporcional a su desplazamiento. Esta ecuación se puede resolver para determinar la posición y la velocidad del objeto en función del tiempo.
2. Circuitos eléctricos
En el campo de los circuitos eléctricos, las ecuaciones diferenciales de segundo orden con términos exponenciales y constantes son esenciales para analizar el comportamiento de circuitos con componentes inductivos y capacitivos. Por ejemplo, en un circuito RLC serie, la corriente puede describirse mediante una ecuación diferencial de segundo orden que tiene términos exponenciales y constantes relacionados con la resistencia, la capacitancia y la inductancia del circuito. Resolver esta ecuación permite determinar el comportamiento transitorio y el estado estable del circuito.
3. Dinámica de fluidos
En la dinámica de fluidos, las ecuaciones diferenciales de segundo orden con términos exponenciales y constantes se utilizan para modelar el flujo de fluidos en diferentes situaciones. Por ejemplo, la ecuación de Bernoulli, que describe el flujo de un fluido incompresible a lo largo de una línea de corriente, es una ecuación diferencial de segundo orden que puede resolverse para determinar la velocidad del fluido en diferentes puntos.
4. Vibraciones mecánicas
En el estudio de las vibraciones mecánicas, las ecuaciones diferenciales de segundo orden con términos exponenciales y constantes son cruciales para entender el comportamiento de sistemas vibrantes. Por ejemplo, el sistema masa-resorte-amortiguador se describe mediante una ecuación diferencial de segundo orden que tiene términos exponenciales y constantes relacionados con la masa, la constante del resorte y el coeficiente de amortiguamiento. Resolver esta ecuación proporciona información sobre la frecuencia natural, la amplitud y la respuesta del sistema ante excitaciones externas.
En resumen, las ecuaciones diferenciales de segundo orden con términos exponenciales y constantes tienen una amplia variedad de aplicaciones en la ciencia y la ingeniería, permitiendo describir y analizar fenómenos físicos y naturales de manera precisa.
Conclusiones
Las conclusiones son una parte fundamental de cualquier texto, ya que nos permiten resumir y destacar los puntos clave expuestos anteriormente. A continuación, se presentan las principales conclusiones extraídas del análisis realizado:
1. Importancia de las etiquetas HTML
Las etiquetas HTML son fundamentales para estructurar y dar formato a nuestro contenido web. El uso adecuado de etiquetas como <strong> permite resaltar visualmente las frases más importantes y enfatizar su significado para el lector.
2. Uso de encabezados y listas
Los encabezados, como <h3>, son esenciales para organizar y jerarquizar la información en un texto. Además, las listas en HTML nos ayudan a presentar datos de manera ordenada y fácil de leer para el usuario.
3. Poder de las negritas
El uso de negritas, representado por la etiqueta <b>, es una herramienta eficaz para resaltar términos, ideas o frases relevantes. Las negritas captan la atención del lector y le permiten identificar rápidamente los puntos más destacados del texto.
En resumen, el uso adecuado de etiquetas HTML, como <strong>, junto con encabezados, listas y negritas, contribuye a mejorar la legibilidad y comprensión del contenido web. Estas herramientas permiten destacar la información esencial y guiar al lector a través del texto de manera efectiva.