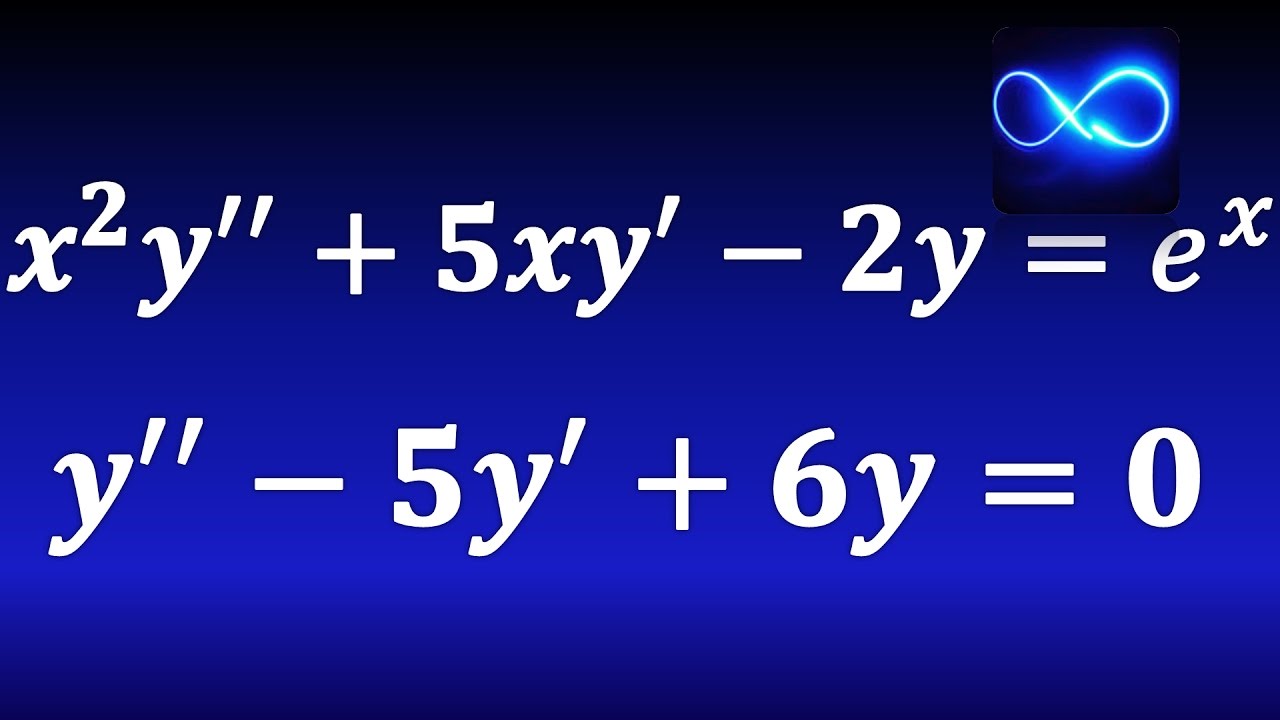Ecuación diferencial de segundo orden sin términos lineales

Una ecuación diferencial de segundo orden sin términos lineales es una ecuación diferencial en la que la segunda derivada de la función desconocida es la única derivada presente y no hay términos lineales.

Anuncios

En matemáticas, una ecuación diferencial es una ecuación que relaciona una función desconocida con sus derivadas. En particular, las ecuaciones diferenciales de segundo orden son aquellas en las que la segunda derivada de la función desconocida aparece en la ecuación.

Por otro lado, los términos lineales en una ecuación diferencial son aquellos que involucran la función desconocida y sus derivadas de primer orden. Estos términos pueden ser multiplicados por una constante o una función de la variable independiente.

Por lo tanto, una ecuación diferencial de segundo orden sin términos lineales se refiere a una ecuación en la que solo aparece la segunda derivada de la función desconocida y no hay términos que involucren las derivadas de primer orden.

Estas ecuaciones diferenciales son de gran importancia en diversos campos de la física y la ingeniería, ya que modelan fenómenos en los que la aceleración es la única fuerza presente. Algunos ejemplos de ecuaciones diferenciales de segundo orden sin términos lineales son la ecuación del oscilador armónico simple y la ecuación de Laplace en electrostática.

Anuncios

Aplicaciones de las ecuaciones diferenciales de segundo orden sin términos lineales

Las ecuaciones diferenciales de segundo orden sin términos lineales tienen numerosas aplicaciones en diversas áreas:

Física y mecánica:

Movimiento armónico simple: Las ecuaciones diferenciales de segundo orden sin términos lineales son fundamentales en el estudio del movimiento armónico simple. Este tipo de movimiento se encuentra en sistemas que oscilan alrededor de una posición de equilibrio, como un péndulo o un resorte. Se pueden modelar utilizando ecuaciones diferenciales de segundo orden sin términos lineales.
Vibraciones mecánicas: Las ecuaciones diferenciales de segundo orden sin términos lineales también son útiles en el estudio de las vibraciones mecánicas, como las vibraciones de puentes o edificios. Estas vibraciones se pueden describir mediante modelos matemáticos que involucran ecuaciones diferenciales de segundo orden sin términos lineales.
Oscilaciones eléctricas: En circuitos eléctricos, las ecuaciones diferenciales de segundo orden sin términos lineales son utilizadas para analizar el comportamiento de las oscilaciones eléctricas en elementos como los capacitores o inductores.

Ingeniería y control:

Sistemas dinámicos: Los sistemas dinámicos presentes en la ingeniería y el control se pueden modelar con ecuaciones diferenciales de segundo orden sin términos lineales. Esto permite estudiar el comportamiento de sistemas complejos y predecir su evolución en el tiempo.
Análisis de estructuras: Las ecuaciones diferenciales de segundo orden sin términos lineales son indispensables en el análisis de estructuras como puentes, edificios o pórticos. Estas ecuaciones permiten determinar su respuesta frente a cargas externas y evaluar la estabilidad de la estructura.

Otras aplicaciones:

Biología: En biología, las ecuaciones diferenciales de segundo orden sin términos lineales se utilizan para describir fenómenos como el crecimiento de poblaciones o las oscilaciones en los ritmos biológicos.
Economía: Las ecuaciones diferenciales de segundo orden sin términos lineales también encuentran aplicación en la economía, permitiendo modelar y predecir el comportamiento de variables económicas, como la inflación o el crecimiento económico.

En conclusión, las ecuaciones diferenciales de segundo orden sin términos lineales son herramientas fundamentales en diversas áreas de estudio, tanto en ciencias naturales como en ingeniería y economía. Su utilización permite comprender y predecir el comportamiento de sistemas dinámicos y fenómenos oscilatorios.

Anuncios

Métodos de resolución de ecuaciones diferenciales de segundo orden sin términos lineales

En el estudio de las ecuaciones diferenciales de segundo orden sin términos lineales, existen diferentes métodos para su resolución. Estos métodos nos permiten encontrar soluciones particulares que satisfacen la ecuación diferencial dada.

Método del factor integrante

El método del factor integrante es utilizado cuando la ecuación diferencial puede ser transformada en una forma donde su solución se obtiene al multiplicar ambos lados de la ecuación por un factor integrante adecuado.

El factor integrante se elige de tal manera que al multiplicar la ecuación diferencial por este factor, la ecuación se pueda reescribir de forma que pueda ser integrada más fácilmente. Al obtener la integral, se obtiene la solución de la ecuación diferencial original.

Variación de parámetros

El método de variación de parámetros es utilizado cuando ya se conoce una solución particular de la ecuación diferencial homogénea asociada. Si se tiene una solución particular de la ecuación homogénea, la cual no contiene los términos no homogéneos, se puede encontrar una solución particular para la ecuación diferencial completa.

Para aplicar este método, se asume que la solución particular puede ser escrita como una combinación lineal de la solución particular de la ecuación homogénea y una función desconocida multiplicada por el factor integrante.

Método de coeficientes indeterminados

El método de coeficientes indeterminados es utilizado cuando la ecuación diferencial de segundo orden sin términos lineales tiene términos no homogéneos que pueden ser expresados como una función algebraica, exponencial, trigonométrica o una combinación de ellas.

Este método consiste en adivinar una solución particular y sustituirla en la ecuación diferencial. A través de manipulaciones algebraicas, se determinan los coeficientes que hacen que la solución adivinada satisfaga la ecuación diferencial.

Método del operador diferencial

El método del operador diferencial es utilizado cuando la ecuación diferencial puede ser expresada como una relación entre el operador diferencial y la función desconocida.

Este método consiste en representar al operador diferencial en términos de funciones elementales, como el seno, coseno o exponenciales, y luego encontrar una solución que satisfaga la relación entre el operador diferencial y la función desconocida.

En resumen, los métodos de resolución de ecuaciones diferenciales de segundo orden sin términos lineales son herramientas útiles para encontrar soluciones particulares que satisfacen estas ecuaciones. El método del factor integrante, la variación de parámetros, el método de coeficientes indeterminados y el método del operador diferencial ofrecen diferentes enfoques para abordar la resolución de este tipo de ecuaciones diferenciales.

Ejemplo de resolución de una ecuación diferencial de segundo orden sin términos lineales

Introducción

En el campo de las matemáticas, especialmente en el cálculo diferencial, una ecuación diferencial es una ecuación que relaciona una función desconocida y sus derivadas. En este blog post, vamos a resolver un ejemplo de una ecuación diferencial de segundo orden sin términos lineales.

Definición de una ecuación diferencial de segundo orden sin términos lineales

Una ecuación diferencial de segundo orden sin términos lineales se puede representar matemáticamente de la siguiente manera:

y”(x) = f(x)

Donde y”(x) es la segunda derivada de la función desconocida y(x) con respecto a x, y f(x) es una función dada sin términos lineales.

Resolución del ejemplo

Para resolver la ecuación diferencial de segundo orden sin términos lineales, debemos seguir los siguientes pasos:

Obtener la función y(x) desconocida.
Encontrar la segunda derivada y”(x).
Escribir la ecuación diferencial sin términos lineales, reemplazando y”(x) por f(x).
Resolver la ecuación obtenida.

Veamos un ejemplo paso a paso:

Obtener la función y(x) desconocida: Supongamos que tenemos la ecuación y”(x) = sin(x). Queremos encontrar la función y(x).
Encontrar la segunda derivada y”(x): La segunda derivada de y(x) es y”(x).
Escribir la ecuación diferencial sin términos lineales: Reemplazamos y”(x) por f(x) en la ecuación: sin(x) = f(x).
Resolver la ecuación obtenida: En este caso, la función f(x) es igual a sin(x), por lo que la solución de la ecuación diferencial sería y(x) = -cos(x) más una constante de integración.

En conclusión, hemos resuelto con éxito un ejemplo de una ecuación diferencial de segundo orden sin términos lineales. La clave para resolver este tipo de ecuaciones es identificar los pasos mencionados anteriormente y aplicar los conceptos adecuados de cálculo diferencial.