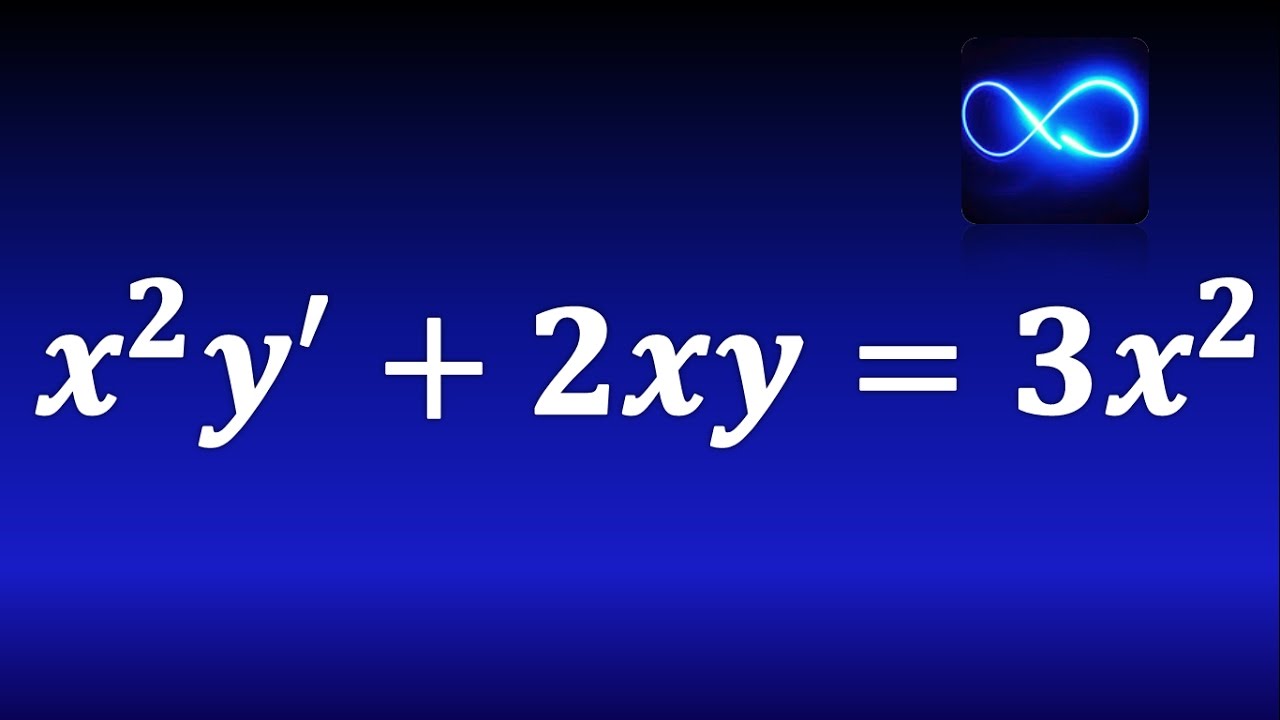La ecuación diferencial lineal de primer orden con coeficientes variables es un concepto fundamental en el campo de las matemáticas y la física. Este tipo de ecuación diferencial aparece en una variedad de aplicaciones, desde circuitos eléctricos hasta la mecánica cuántica. En este artículo, exploraremos en detalle esta clase de ecuaciones diferenciales, su resolución paso a paso y su relevancia en diversos contextos.
Definición de la ecuación diferencial
Una ecuación diferencial lineal de primer orden con coeficientes variables tiene la forma general ( frac{dy}{dx} + P(x)y = Q(x) ), donde ( P(x) ) y ( Q(x) ) son funciones continuas definidas en un intervalo ( I ). La incógnita es la función ( y = y(x) ) que satisface esta ecuación diferencial en el intervalo ( I ).
Conceptos fundamentales
Antes de adentrarnos en la resolución de este tipo de ecuaciones diferenciales, es crucial comprender algunos conceptos fundamentales. La idea central detrás de estas ecuaciones es la relación entre la tasa de cambio de una función y la función misma, en función de variables independientes complejas.
Coeficientes variables
La presencia de coeficientes variables en la ecuación diferencial añade un grado de complejidad significativo. Mientras que en las ecuaciones con coeficientes constantes, los términos ( P(x) ) y ( Q(x) ) son constantes reales, en este caso, pueden variar con respecto a la variable ( x ). Esta variabilidad introduce desafíos únicos en la resolución, pero también permite modelar sistemas más realistas y diversos.
Aplicaciones en física y ingeniería
Las ecuaciones diferenciales de primer orden con coeficientes variables son de suma importancia en aplicaciones prácticas. En física, por ejemplo, estas ecuaciones son la base para comprender el comportamiento de circuitos eléctricos complejos, así como en la mecánica cuántica moderna. En ingeniería, se utilizan para describir fenómenos como la transferencia de calor y la dinámica de fluidos, entre otros.
Resolución paso a paso
Ahora, abordemos la resolución de la ecuación diferencial lineal de primer orden con coeficientes variables. Este proceso implica el uso de diferentes técnicas, como la integración y la manipulación algebraica, para encontrar la solución general de la ecuación diferencial.
Método de integración directa
Comenzaremos aplicando el método de integración directa para resolver la ecuación diferencial. Este enfoque implica reorganizar la ecuación y luego integrar ambos lados con respecto a la variable ( x ). Al integrar ( frac{dy}{dx} + P(x)y = Q(x) ), obtenemos ( y = e^{-int P(x)dx} left( int Q(x)e^{int P(x)dx} dx + C right) ), donde ( C ) es la constante de integración.
Factor integrante
En el caso de coeficientes variables, el método del factor integrante es crucial. Este enfoque implica encontrar un factor ( mu(x) ) tal que al multiplicar toda la ecuación diferencial por ( mu(x) ), se transforme en una expresión exacta, lo que facilita su solución. El factor integrante está dado por ( mu(x) = e^{int P(x)dx} ), lo que nos lleva a la forma estándar de la ecuación diferencial lineal.
Aplicación del factor integrante
Al multiplicar la ecuación diferencial ( frac{dy}{dx} + P(x)y = Q(x) ) por el factor integrante ( mu(x) = e^{int P(x)dx} ), obtenemos la forma exacta ( frac{d}{dx} left( y mu(x) right) = Q(x) mu(x) ). A partir de aquí, podemos encontrar la solución general integrando ambos lados de la ecuación.
Ejemplo numérico
Para ilustrar estos conceptos, consideremos la ecuación diferencial ( frac{dy}{dx} + frac{2}{x}y = x ). En este caso, ( P(x) = frac{2}{x} ) y ( Q(x) = x ). Aplicando el factor integrante ( mu(x) = e^{int frac{2}{x}dx} = e^{2ln|x|} = x^2 ), la ecuación se transforma en ( frac{d}{dx} left( xy^2 right) = x^3 ). La solución general puede encontrarse integrando ambos lados de la ecuación transformada.
La ecuación diferencial lineal de primer orden con coeficientes variables es un tema matemático y físico apasionante, con aplicaciones significativas en una variedad de campos. Su resolución paso a paso requiere el dominio de técnicas como la integración directa y el factor integrante. Comprender esta clase de ecuaciones es esencial para abordar problemas tanto teóricos como prácticos en diversos contextos científicos y tecnológicos.