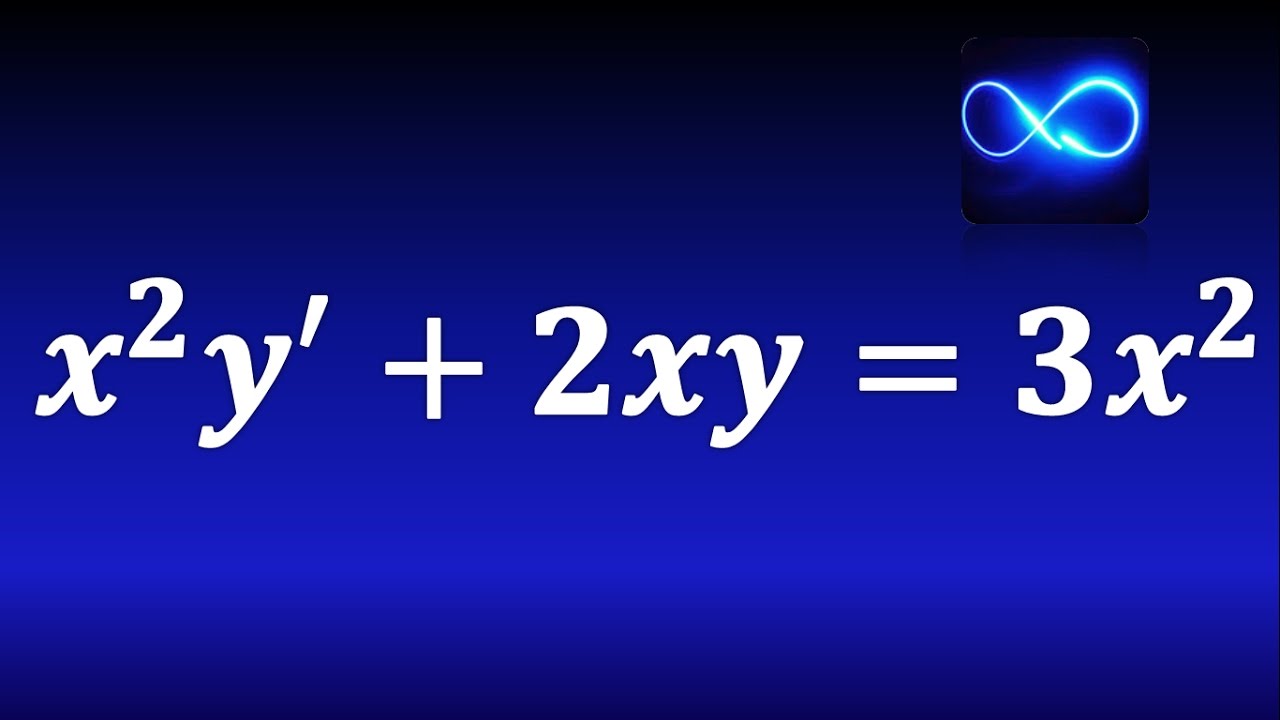Una ecuación diferencial lineal de primer orden es una ecuación en la que la variable independiente y su derivada de primer orden están presentes. Este tipo de ecuaciones es fundamental en matemáticas y tiene diversas aplicaciones en la física, ingeniería, economía, entre otros campos.
Diferenciación implícita y soluciones generales
Al enfrentarnos a una ecuación diferencial lineal de primer orden, es común utilizar la técnica de diferenciación implícita para separar las variables y luego proceder a integrar. La solución general de una ecuación diferencial de este tipo es una función que involucra una constante arbitraria, conocida como constante de integración. Esta constante se determina mediante condiciones iniciales o condiciones de contorno específicas del problema.
Aplicación en problemas de crecimiento poblacional
Una de las aplicaciones comunes de las ecuaciones diferenciales lineales de primer orden es en el modelado del crecimiento poblacional. Supongamos que la tasa de cambio de una población en un momento dado es proporcional a la cantidad de individuos en la población. Esta situación se puede modelar utilizando una ecuación diferencial lineal de primer orden, donde la población se representa como una función de la variable independiente (tiempo) y su derivada.
Razón de cambio y pendiente de la curva solución
Al resolver una ecuación diferencial lineal de primer orden, es importante comprender que la solución es una curva en el plano xy. La derivada de la solución en un punto dado proporciona la razón de cambio en ese punto, lo que a su vez representa la pendiente de la curva solución en ese punto. Esta interpretación geométrica es esencial para comprender el comportamiento de las soluciones en diferentes contextos.
Resolución paso a paso
Veamos ahora un proceso detallado para resolver una ecuación diferencial lineal de primer orden con variables x e y. Utilizaremos un ejemplo concreto para ilustrar el procedimiento paso a paso.
Paso 1: Reconocer el tipo de ecuación
Lo primero que debemos hacer al enfrentarnos a una ecuación diferencial es identificar su tipo. En el caso de una ecuación diferencial lineal de primer orden con variables x e y, debemos verificar si la ecuación puede escribirse en la forma estándar y’ + p(x)y = q(x), donde p(x) y q(x) son funciones conocidas.
Paso 2: Integrar el factor integrante
Si la ecuación se puede escribir en la forma estándar mencionada, el siguiente paso consiste en determinar el factor integrante, que se calcula como e^∫p(x)dx. Este factor integrante nos permite transformar la ecuación original en una forma que simplifica el proceso de integración.
Paso 3: Multiplicar la ecuación por el factor integrante
Una vez que hemos encontrado el factor integrante, multiplicamos toda la ecuación diferencial por este factor. Este paso es fundamental para convertir la ecuación en una forma que facilite la integración, ya que nos permite aplicar la regla de la cadena de forma efectiva.
Paso 4: Integrar ambos lados de la ecuación
Después de aplicar el factor integrante a la ecuación, procedemos a integrar ambos lados con respecto a x. Esto implica encontrar la integral de las expresiones que involucran a y, así como la integral de la función q(x) que aparece en el lado derecho de la ecuación.
Paso 5: Resolver para y
Una vez que hemos integrado ambos lados de la ecuación, llegamos a una expresión que relaciona y con x. Despejando y en esta expresión, obtenemos la solución general de la ecuación diferencial lineal de primer orden. Es importante recordar incluir la constante de integración al resolver para y, ya que esta constante determinará la solución específica del problema.
Paso 6: Aplicar condiciones iniciales (si es necesario)
En muchos casos, necesitamos aplicar condiciones iniciales o de contorno para encontrar la solución única de la ecuación diferencial. Estas condiciones pueden proporcionarse en forma de valores específicos de y para un cierto valor de x, o pueden estar relacionadas con otras restricciones del problema. Al aplicar estas condiciones, determinamos los valores precisos de las constantes de integración y obtenemos la solución particular que cumple con las condiciones dadas.
Las ecuaciones diferenciales lineales de primer orden con variables x e y son herramientas fundamentales en matemáticas y aplicaciones científicas. Al comprender cómo resolver estas ecuaciones paso a paso, podemos abordar una amplia gama de problemas que involucran tasas de cambio, crecimiento, decaimiento y otros fenómenos dinámicos. La interpretación geométrica de las soluciones y su relación con el campo de pendientes nos proporciona una comprensión más profunda de los conceptos subyacentes y sus aplicaciones prácticas.