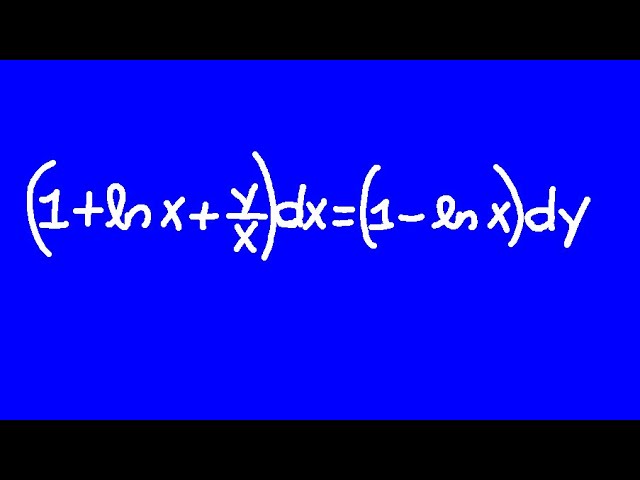La ecuación diferencial (1+ln x+y/x)dx=(1-ln x)dy es un problema que ha intrigado a matemáticos y científicos durante mucho tiempo, debido a su complejidad y a las múltiples aplicaciones en la modelización de fenómenos naturales.
En este artículo, exploraremos detalladamente cómo abordar esta ecuación diferencial, paso a paso, para encontrar su solución. A través de un análisis exhaustivo y cuidadoso, descubriremos las técnicas y conceptos matemáticos necesarios para resolver este desafiante problema.
Análisis de la ecuación diferencial
Antes de comenzar a abordar la solución de la ecuación diferencial, es fundamental realizar un análisis detallado de sus componentes. La ecuación (1+ln x+y/x)dx=(1-ln x)dy puede parecer intimidante a primera vista, pero al descomponerla y comprender su estructura, podemos identificar los enfoques matemáticos que nos llevarán hacia la solución.
Separación de variables
Un enfoque común para resolver ecuaciones diferenciales es la técnica de separación de variables. En el caso de nuestra ecuación diferencial, buscaremos manipularla para lograr aislar las variables y luego integrar cada lado por separado. Este proceso nos permitirá desentrañar la solución deseada a partir de la ecuación dada.
Manipulación algebraica
La manipulación algebraica es una habilidad esencial en la resolución de ecuaciones diferenciales. Al trabajar con la ecuación (1+ln x+y/x)dx=(1-ln x)dy, emplearemos técnicas algebraicas para reorganizar los términos y expresiones, de modo que podamos aplicar métodos de integración de manera efectiva.
Métodos de integración
Una vez que hayamos logrado separar las variables y aplicar la manipulación algebraica necesaria, nos encontraremos en una posición para llevar a cabo la integración de cada lado de la ecuación diferencial. Examinaremos diferentes métodos de integración, como la integración por partes o la integración trigonométrica, en busca de la solución que buscamos.
Resolución paso a paso
Ahora que hemos establecido un marco teórico y estratégico para abordar la ecuación diferencial, es el momento de adentrarnos en la resolución paso a paso. En cada etapa, explicaremos con detalle las operaciones y transformaciones realizadas, con el objetivo de brindar una comprensión clara y completa del proceso de solución.
Consideraciones adicionales
Además de los enfoques específicos mencionados anteriormente, nos detendremos en consideraciones adicionales que pueden surgir durante el proceso de resolución. Esto puede incluir la identificación de condiciones iniciales, la interpretación de la solución en el contexto del problema original y la verificación de la solución encontrada.
Conclusiones
Tras completar el proceso de resolución y abordar todas las consideraciones pertinentes, llegaremos a conclusiones significativas sobre la solución de la ecuación diferencial (1+ln x+y/x)dx=(1-ln x)dy. Reflexionaremos sobre los resultados obtenidos, destacando la importancia y las implicaciones de la solución encontrada en el contexto matemático y aplicado.
En resumen, este artículo ofrece una inmersión profunda en la resolución de la ecuación diferencial (1+ln x+y/x)dx=(1-ln x)dy, proporcionando a los lectores una comprensión paso a paso de este desafiante problema matemático. A través de un enfoque detallado y exhaustivo, exploramos las técnicas y conceptos necesarios para abordar esta ecuación diferencial, ofreciendo una experiencia enriquecedora para aquellos que buscan dominar este campo de las matemáticas.