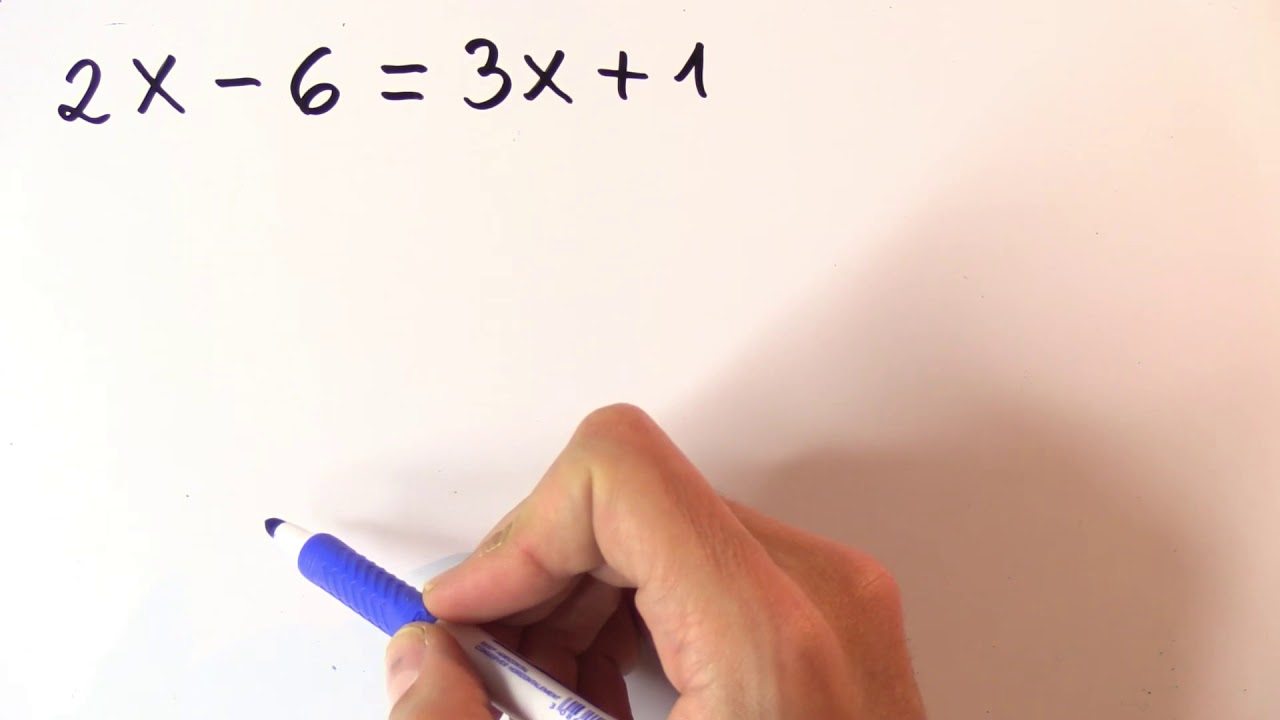1. ¿Qué es una ecuación lineal?
Una ecuación lineal es una expresión matemática en la cual las variables presentes están elevadas a la primera potencia y se relacionan entre sí mediante operaciones de suma, resta y multiplicación. En su forma más simple, una ecuación lineal se puede representar como:
ax + b = c
Donde a, b y c son constantes conocidas, y x es la variable que se busca determinar.
Las ecuaciones lineales son fundamentales en la resolución de problemas matemáticos y se utilizan en diversas disciplinas como la física, la economía y la ingeniería, entre otras.
Las incógnitas en una ecuación lineal pueden representar cantidades físicas, económicas o abstractas, y su resolución permite encontrar el valor de estas incógnitas, lo que ayuda a entender mejor diversos fenómenos y situaciones.
Asimismo, las ecuaciones lineales se pueden expresar en diferentes formas, como la forma estándar, la forma general o la forma pendiente-intersección. Estas diferentes formas permiten analizar y resolver problemas desde distintos enfoques.
En conclusión, una ecuación lineal es una expresión matemática que involucra variables elevadas a la primera potencia y se resuelve encontrando el valor de dichas variables. Son fundamentales en diferentes áreas y permiten modelar y resolver problemas de manera eficiente.
2. Pasos para resolver la ecuación lineal
2. Pasos para resolver la ecuación lineal
3. Desarrollando la ecuación 5x + 3 = 2x – 6
Desarrollando la ecuación 5x + 3 = 2x – 6
4. Simplificando la ecuación
En esta cuarta sección, nos adentraremos en el proceso de simplificar la ecuación en cuestión. Para ello, utilizaremos varias herramientas y técnicas que nos permitirán llegar a la forma más simplificada posible.
Una de las primeras cosas que debemos hacer es identificar los términos que podemos simplificar. Esto implica buscar aquellos términos que sean equivalentes o que se puedan combinar de alguna manera.
Una vez identificados los términos, podemos utilizar propiedades de las operaciones para simplificarlos. Esto incluye las propiedades de suma, resta, multiplicación y división. Por ejemplo, si tenemos dos términos que se suman entre sí, podemos combinarlos en uno solo.
Otra técnica que podemos utilizar es el uso de fórmulas y reglas matemáticas. Estas fórmulas son herramientas útiles que nos permiten simplificar ecuaciones específicas. Por ejemplo, la fórmula de la suma de cuadrados nos permite simplificar expresiones de ese tipo.
Además, podemos utilizar el concepto de razones equivalentes para simplificar la ecuación. Esto implica encontrar una fracción equivalente con un denominador más simple o un numerador más simple.
En algunos casos, puede ser necesario utilizar sustituciones para simplificar la ecuación. Esto implica reemplazar una variable o término por otro que sea más fácil de manejar o simplificar. Por ejemplo, podemos sustituir una expresión compleja por una variable única.
Finalmente, es importante recordar que la simplificación de una ecuación no siempre significa llegar a una forma totalmente simplificada. Dependiendo del problema y el contexto, puede ser aceptable dejar la ecuación en una forma más general o hacer aproximaciones.
En resumen, simplificar una ecuación implica identificar los términos que se pueden combinar o simplificar, utilizar propiedades, fórmulas y reglas matemáticas, aplicar razones equivalentes y, en algunos casos, hacer sustituciones. La simplificación no siempre implica llegar a una forma totalmente simplificada, sino que depende del problema y el contexto.
5. Solución de la ecuación lineal
La solución de una ecuación lineal se obtiene al encontrar el valor de la variable que satisface esa ecuación. En general, una ecuación lineal tiene la forma ax + b = c, donde a, b y c son coeficientes constantes y x es la variable.
Para resolver una ecuación lineal, se pueden realizar diversas operaciones algebraicas con el objetivo de aislar la variable en un lado de la ecuación. Estas operaciones incluyen sumar o restar términos en ambos lados de la ecuación, multiplicar o dividir por constantes y despejar la variable.
Por ejemplo, consideremos la ecuación 2x + 3 = 7. Para resolverla, podemos comenzar restando 3 a ambos lados de la ecuación:
- 2x + 3 – 3 = 7 – 3
- 2x = 4
A continuación, podemos dividir ambos lados de la ecuación por 2 para despejar la variable x:
- 2x / 2 = 4 / 2
- x = 2
Por lo tanto, la solución de la ecuación es x = 2. Esto significa que si sustituimos el valor de x por 2 en la ecuación original, obtendremos una igualdad verdadera.
En resumen, la solución de una ecuación lineal se obtiene al realizar operaciones algebraicas con el objetivo de aislar la variable. Es importante seguir las reglas del álgebra y realizar las mismas operaciones en ambos lados de la ecuación para mantener el equilibrio. Al final, obtendremos el valor de la variable que satisface la ecuación dada.