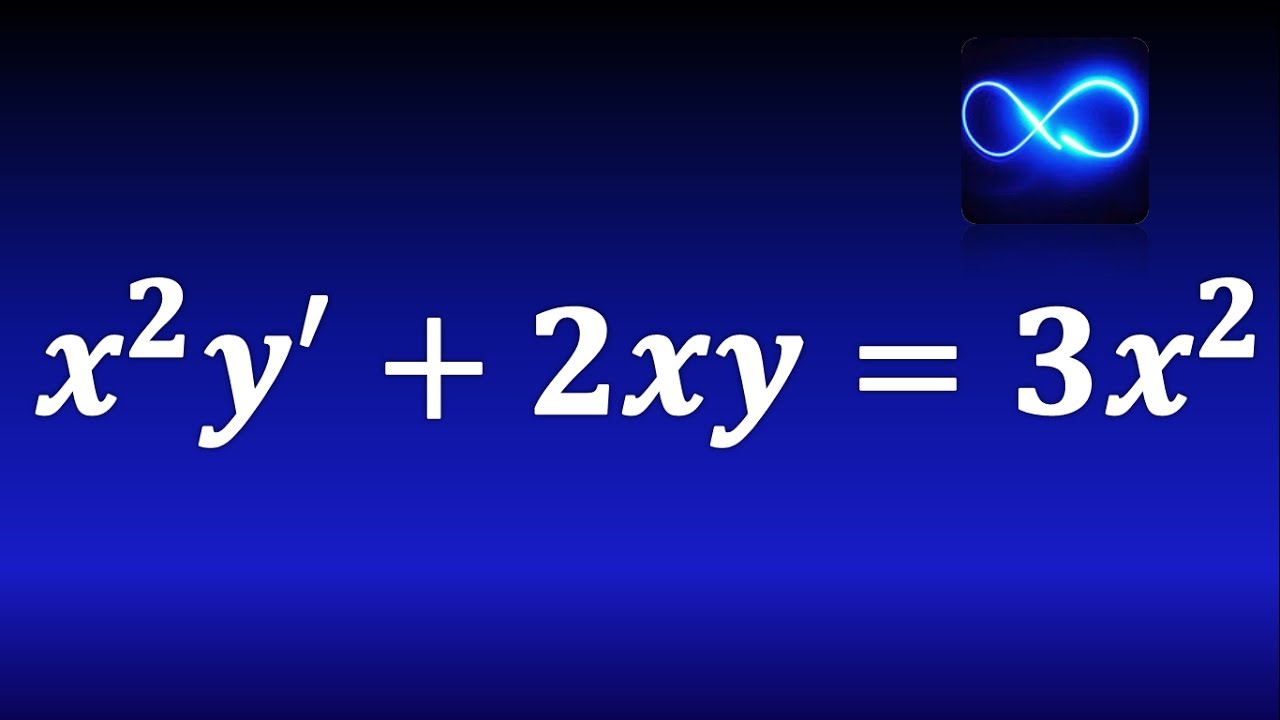Ejemplos resueltos de ecuaciones diferenciales de primer orden

1. Ejemplo de ecuación diferencial lineal:

En matemáticas, una ecuación diferencial lineal es una ecuación que involucra una función desconocida y sus derivadas lineales de primer orden.

Un ejemplo común de una ecuación diferencial lineal es la ecuación diferencial lineal homogénea de primer orden:

dy/dx + p(x)y = 0

donde y es la función desconocida, x es la variable independiente y p(x) es una función conocida.

La solución general de esta ecuación se puede encontrar utilizando métodos de integración elemental, lo que conduce a una solución en términos de una constante arbitraria.

Por ejemplo, si p(x) = x, la ecuación diferencial se convierte en:

dy/dx + x*y = 0

Esta ecuación tiene una solución general de la forma:

y = Ce^-x2/2

donde C es una constante arbitraria.

Resumen:

Una ecuación diferencial lineal es aquella que involucra una función desconocida y sus derivadas lineales de primer orden. La solución general de estas ecuaciones se puede encontrar utilizando métodos de integración elemental. Un ejemplo común de una ecuación diferencial lineal es la ecuación diferencial lineal homogénea de primer orden, que tiene una solución en términos de una constante arbitraria.

2. Ejemplo de ecuación diferencial separable:

En el estudio de las ecuaciones diferenciales, uno de los tipos más comunes y más sencillos de resolver es la ecuación diferencial separable. Para comprender mejor este concepto, veamos un ejemplo:

Ejemplo:

Consideremos la siguiente ecuación diferencial:

dy/dx = x^2 + y^2

Para resolver esta ecuación, primero debemos separar las variables. En este caso, podemos separar las variables x e y de la siguiente manera:

dy/(y^2) = (x^2)dx

A continuación, podemos integrar ambos lados de la ecuación con respecto a sus variables:

∫(1/y^2)dy = ∫(x^2)dx

Integrando el lado izquierdo:

-1/y = (1/3)x^3 + C1

Donde C1 es una constante de integración.

Para simplificar la ecuación, multiplicamos ambos lados por -1 y obtenemos:

1/y = -(1/3)x^3 – C1

Ahora podemos despejar y:

y = 1/(-(1/3)x^3 – C1)

Podemos simplificar aún más esta ecuación:

y = -3/(x^3 + 3C1)

Por lo tanto, la solución general de la ecuación diferencial es:

y = -3/(x^3 + 3C1)

En conclusión, este es un ejemplo de una ecuación diferencial separable que hemos resuelto paso a paso. La técnica de separar variables y luego integrar cada lado de la ecuación nos permite encontrar la solución general de la ecuación diferencial.

3. Ejemplo de ecuación diferencial exacta:

En matemáticas, una ecuación diferencial exacta es aquella en la que se puede encontrar una función que es su derivada. Su forma general es:

M(x, y) dx + N(x, y) dy = 0

donde M(x, y) y N(x, y) son funciones de dos variables.

Un ejemplo sencillo de este tipo de ecuación es:

2x dx + (3x² + 2y) dy = 0

Para resolver esta ecuación, se deben seguir los siguientes pasos:

1. Comprobar que la ecuación es exacta, es decir, que se cumpla la condición:

∂M/∂y = ∂N/∂x

2. Encontrar una función φ(x, y) tal que φx(x, y) = M(x, y) y φy(x, y) = N(x, y).
3. Integrar φx con respecto a x y φy con respecto a y, respetando las constantes de integración.
4. Igualar las expresiones resultantes y simplificar la ecuación.
5. Resolver la ecuación simplificada y encontrar la solución general.

En el ejemplo dado, se puede verificar que se cumple la condición de exactitud y encontrar fácilmente la función φ(x, y) = x² + x³y, que satisface las condiciones requeridas en el paso 2.

Integrando φx = 2x con respecto a x, se obtiene:

∫(∂φ/∂x) dx = ∫(2x) dx = x² + C1(y)

donde C1(y) es una constante de integración que depende de y.

Integrando φy = 3x² + 2y con respecto a y, se obtiene:

∫(∂φ/∂y) dy = ∫(3x² + 2y) dy = 3x²y + y² + C2(x)

donde C2(x) es una constante de integración que depende de x.

Igualando las expresiones resultantes y simplificando, se obtiene:

x² + x³y + C1(y) = 3x²y + y² + C2(x)

Finalmente, resolviendo esta ecuación se encuentra la solución general de la ecuación diferencial exacta dada.

En conclusión, las ecuaciones diferenciales exactas son un tema importante en el campo de las matemáticas y se pueden resolver siguiendo un conjunto de pasos específicos. En el ejemplo dado, se mostró el proceso de solución para una ecuación diferencial exacta sencilla.

4. Ejemplo de ecuación diferencial de variables separables:

En el estudio de las ecuaciones diferenciales, se pueden encontrar diferentes métodos de resolución, uno de ellos es el método de variables separables. Este método se utiliza cuando una ecuación diferencial se puede reescribir en la forma:

dy/dx = f(x)g(y)

donde f(x) es una función de x y g(y) es una función de y.

Para ilustrar este método, consideremos el siguiente ejemplo:

1. Paso 1: Reescribimos la ecuación en la forma dy/dx = f(x)g(y). Digamos que tenemos la ecuación diferencial 3x^2ydy = 4y^3dx.
2. Paso 2: Separamos las variables. En este caso, podemos dividir ambos lados de la ecuación por y^3 para obtener (3x^2/y^2)dy = 4dx.
3. Paso 3: Integramos ambos lados de la ecuación. Al integrar (3x^2/y^2)dy obtenemos x^2/y = 4x + C, donde C es una constante de integración.
4. Paso 4: Despejamos y en términos de x. En este ejemplo, podemos multiplicar ambos lados de la ecuación por y para obtener x^2 = 4xy + Cy. Luego, podemos despejar y para obtener y = (x^2)/(4x + C).

En conclusión, el método de variables separables es una técnica útil para resolver ecuaciones diferenciales que se pueden expresar en la forma dy/dx = f(x)g(y). Al seguir los pasos mencionados, podemos encontrar una solución general de la ecuación diferencial.

5. Ejemplo de ecuación diferencial homogénea:

Una ecuación diferencial homogénea es aquella en la que todos los términos de la ecuación tienen el mismo grado de la función desconocida y de sus derivadas.

Un ejemplo de ecuación diferencial homogénea es la siguiente:

dy/dx = –(y – x)^2

Para resolver esta ecuación, podemos hacer un cambio de variable, y = vx, de modo que la ecuación se transforma en:

dy/dx = xdv/dx + v

Reemplazando en la ecuación original, obtenemos:

xdv/dx + v = -v^2

Ahora, podemos dividir la ecuación por x y reorganizar los términos para obtener una ecuación separable:

dv/(v^2 + v) = -dx/x

Integrando ambos lados de la ecuación, obtenemos:

-ln(v^2 + v) = -ln(x) + C

Donde C es la constante de integración.

Finalmente, podemos deshacer el cambio de variable para obtener la solución de la ecuación diferencial original:

-ln((y – x)^2 + (y – x)) = -ln(x) + C

Esta es la solución general de la ecuación diferencial homogénea dada.