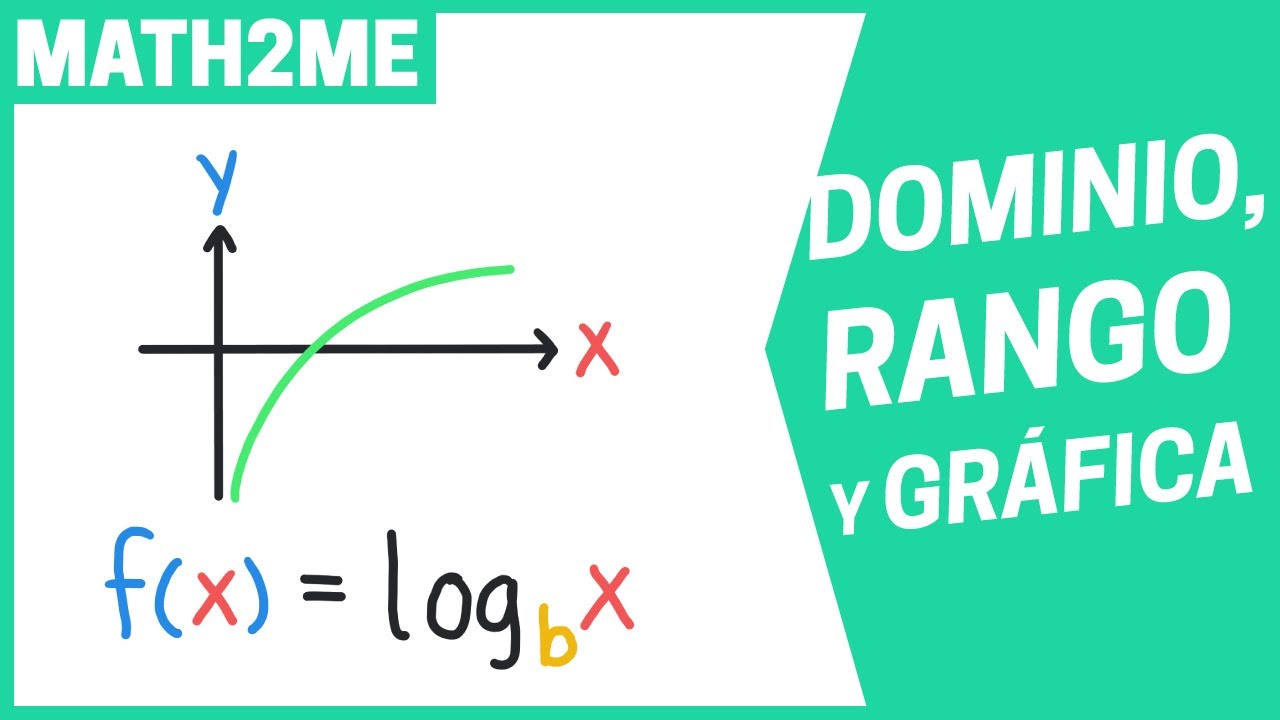
El concepto del rango de una función logarítmica es fundamental para comprender su comportamiento y sus posibles valores. En este artículo, exploraremos en detalle qué es el rango de una función logarítmica, cómo determinarlo y cómo aplicar este conocimiento en contextos matemáticos y del mundo real.
Funciones Logarítmicas
Las funciones logarítmicas son una parte esencial del estudio de las matemáticas. Representan las relaciones entre cantidades que crecen o disminuyen de manera proporcional a una tasa constante. La forma general de una función logarítmica se puede expresar como y = logb(x), donde b es la base del logaritmo y x es el argumento de la función.
Propiedades de las Funciones Logarítmicas
Antes de explorar el rango de una función logarítmica, es importante comprender algunas de sus propiedades fundamentales. Las funciones logarítmicas tienen una serie de características que las distinguen de otras funciones, incluyendo su dominio, su comportamiento asintótico y su comportamiento frente a transformaciones algebraicas.
Dominio de las Funciones Logarítmicas
El dominio de una función logarítmica está determinado por las restricciones impuestas por la base del logaritmo. En general, las funciones logarítmicas tienen un dominio que consiste en todos los números positivos, ya que el logaritmo de cero o un número negativo no está definido en el conjunto de números reales.
Comportamiento Asintótico
El comportamiento asintótico de una función logarítmica es una propiedad importante a considerar al analizar su rango. A medida que el argumento de la función se acerca a cero, la función logarítmica tiende hacia menos infinito. Del mismo modo, a medida que el argumento de la función crece hacia infinito, la función logarítmica crece, pero lo hace cada vez más lentamente.
Rango de una Función Logarítmica
El rango de una función logarítmica se refiere al conjunto de todos los posibles valores de salida de la función. Determinar el rango de una función logarítmica puede proporcionar información crucial sobre su comportamiento y sus aplicaciones en diversos contextos matemáticos y del mundo real.
Rango de la Función Logarítmica Básica
Para comprender el rango de una función logarítmica en su forma más simple, consideremos la función logarítmica con base 10, es decir, y = log10(x). En este caso, el rango de la función logarítmica será el conjunto de todos los números reales. Esto se debe a que, a medida que el argumento x varía, el valor de la función logarítmica puede tomar cualquier valor real.
Rango de la Función Logarítmica con Transformaciones
Cuando la función logarítmica se somete a transformaciones algebraicas, como cambios en la base del logaritmo o desplazamientos verticales u horizontales, su rango puede ser afectado significativamente. Determinar el rango de una función logarítmica transformada requiere un análisis cuidadoso de cómo estas transformaciones afectan la función base y sus posibles valores de salida.
Efecto de Cambios en la Base del Logaritmo
El cambio en la base del logaritmo modifica la pendiente de la función logarítmica y, por lo tanto, puede restringir su rango a un conjunto específico de valores. Por ejemplo, una función logarítmica con una base menor que 1 tendrá un rango limitado a valores negativos, mientras que una base mayor que 1 resultará en un rango exclusivamente positivo.
Desplazamientos Verticales y Horizontales
Los desplazamientos verticales y horizontales de una función logarítmica también influyen en su rango. Un desplazamiento vertical puede cambiar el valor mínimo o máximo que la función puede alcanzar, mientras que un desplazamiento horizontal puede desplazar los valores de entrada para los cuales la función logarítmica alcanza ciertos valores en su rango.
Aplicaciones del Rango de una Función Logarítmica
El rango de una función logarítmica tiene diversas aplicaciones en matemáticas, ciencias naturales, ingeniería, economía y muchas otras disciplinas. Comprender el rango de una función logarítmica puede ayudar a modelar fenómenos del mundo real y tomar decisiones fundamentadas en una variedad de contextos.
Modelado de Crecimiento y Decaimiento
Las funciones logarítmicas se utilizan comúnmente para modelar procesos de crecimiento y decaimiento en campos como la biología, la ecología y la economía. Al determinar el rango de una función logarítmica que representa el crecimiento de una población o el decaimiento de una cantidad específica, se pueden hacer predicciones sobre el comportamiento futuro de estos fenómenos.
Óptimización de Recursos
En ingeniería y economía, el rango de una función logarítmica puede utilizarse para optimizar la asignación de recursos. Al comprender los posibles valores de salida de una función logarítmica que modela el rendimiento de un sistema o el costo de producción, es posible tomar decisiones informadas para maximizar la eficiencia y minimizar los costos.
Análisis de Datos Experimentales
En campos como la física y la química, el rango de una función logarítmica puede ser crucial para analizar datos experimentales. Las relaciones logarítmicas se encuentran a menudo en la naturaleza y comprender su rango puede proporcionar información valiosa sobre los mecanismos subyacentes a fenómenos observados en experimentos.
En resumen, el rango de una función logarítmica es una parte fundamental de su comprensión y aplicación en diversos contextos académicos y del mundo real. Desde su definición básica hasta sus implicaciones en la modelización de fenómenos naturales y la toma de decisiones, el rango de una función logarítmica ofrece un campo fértil para la exploración matemática y científica.