Concepto y propiedades de la parábola
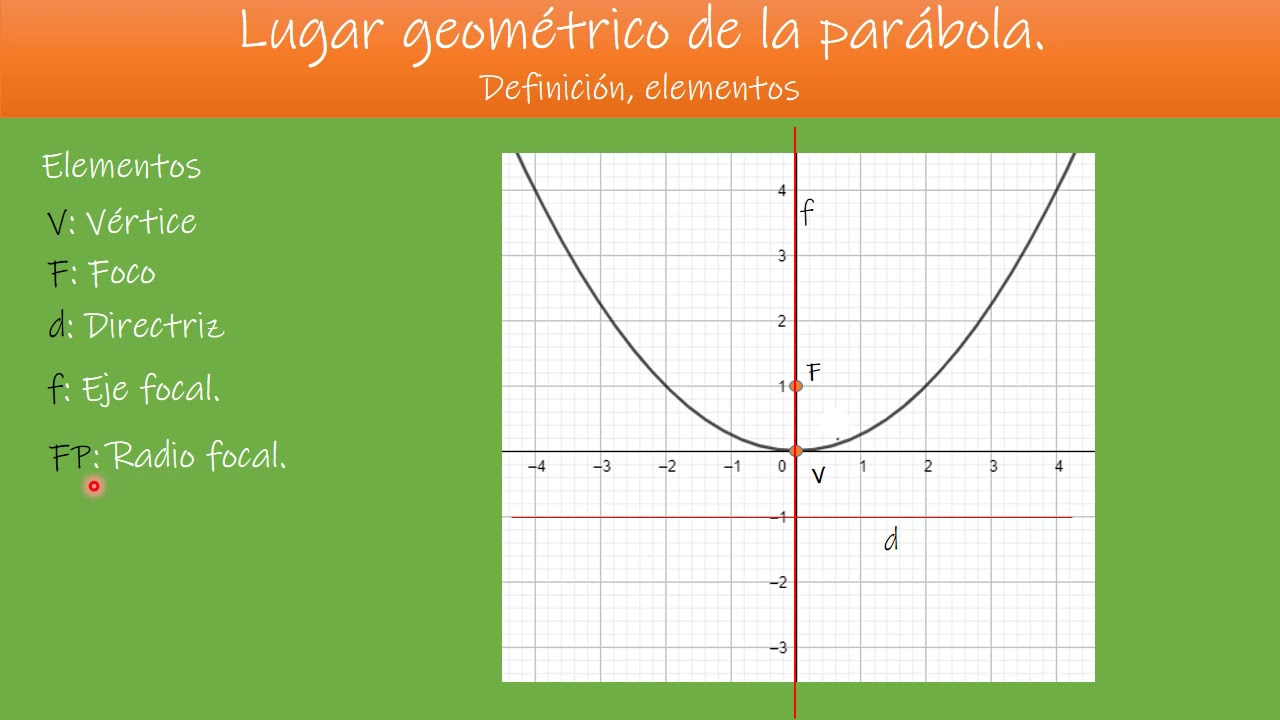
La parábola es una figura geométrica que se define como el conjunto de todos los puntos en un plano que equidistan de un punto fijo, llamado foco, y una recta fija, llamada directriz.
Una de las propiedades más importantes de la parábola es su simetría. La distancia de cualquier punto de la parábola al foco es igual a la distancia de ese punto a la directriz. Esto se conoce como la propiedad focal de la parábola.
Otra propiedad fundamental es la posición del vértice de la parábola. El vértice es el punto más cercano al foco y se encuentra en el eje de simetría de la parábola. Por lo general, se representa como el punto (h, k), donde h y k son las coordenadas del vértice.
Una parábola también es conocida por su excentricidad. La excentricidad de una parábola es siempre igual a 1. Esto significa que la distancia del foco al vértice es igual a la distancia del vértice a la directriz.
Otra característica de la parábola es su forma. Dependiendo del coeficiente que acompaña al término cuadrático en la ecuación de la parábola, esta puede abrir hacia arriba o hacia abajo. Si el coeficiente es positivo, la parábola abre hacia arriba, mientras que si es negativo, la parábola abre hacia abajo.
En resumen, la parábola es una figura geométrica con propiedades únicas, como su simetría, la posición de su vértice, su excentricidad y su forma. Estas propiedades hacen de la parábola una figura fundamental en la geometría y en diversos campos como la física y la óptica.
Ecuación general de la parábola
La ecuación general de la parábola es una forma de representar geométricamente esta figura en el plano cartesiano. Es una ecuación de segundo grado de la forma ax^2 + bx + c = 0, donde a, b y c son constantes.
Existen diferentes maneras de presentar la ecuación general de la parábola en función de la orientación de la misma, es decir, si la parábola está orientada de forma vertical u horizontal.
Para una parábola vertical, la ecuación general toma la forma de y = ax^2 + bx + c. El valor de a determina la apertura de la parábola, siendo positivo para una parábola que se abre hacia arriba y negativo para una parábola que se abre hacia abajo. Los valores de b y c, por su parte, influyen en el desplazamiento horizontal y vertical de la parábola, respectivamente.
En el caso de una parábola horizontal, la ecuación general se presenta como x = ay^2 + by + c. De manera similar que en el caso anterior, el valor de a define la apertura de la parábola, siendo positivo para una parábola que se abre hacia la derecha y negativo para una parábola que se abre hacia la izquierda. Los valores de b y c determinan el desplazamiento horizontal y vertical de la parábola, respectivamente.
En resumen, la ecuación general de la parábola es una forma de representar matemáticamente esta figura geométrica y nos proporciona información sobre su orientación, apertura y desplazamiento en el plano. Es importante comprender cómo modificar los valores de las constantes a, b y c para ajustar la parábola a nuestras necesidades.
Foco y directriz de la parábola
La parábola es un recurso literario utilizado en diversas culturas y tradiciones para transmitir enseñanzas morales, éticas o espirituales de forma sencilla y accesible. En el contexto de la narrativa, la parábola se caracteriza por presentar una historia ficticia que encierra una enseñanza o mensaje profundo.
Uno de los elementos clave en una parábola es el foco, que se refiere al punto central de la historia o la idea principal que se quiere transmitir. El foco es lo que captura la atención del lector o oyente y le permite adentrarse en la trama para descubrir el mensaje subyacente.
Por otro lado, la directriz es el mensaje o enseñanza que se revela a través de la parábola. Es la lección moral, ética o espiritual que se extrae de la historia y que tiene el propósito de transmitir un mensaje profundo y provocar la reflexión en el receptor.
En la parábola, el foco y la directriz están estrechamente relacionados. El foco es el punto de partida que despierta el interés del receptor, mientras que la directriz es lo que se busca transmitir a través de la historia. Ambos elementos son fundamentales para que la parábola cumpla su objetivo de enseñanza y reflexión.
Ejemplo de una parábola:
Imaginemos una parábola que cuenta la historia de un árbol que, a lo largo de las estaciones, va perdiendo sus hojas. El foco de la parábola podría ser la belleza efímera de la naturaleza y la transitoriedad de la vida. Mientras que la directriz podría ser que debemos apreciar los momentos presentes y no aferrarnos al pasado o preocuparnos demasiado por el futuro.
En resumen, la parábola es un recurso literario poderoso que utiliza una historia ficticia para transmitir enseñanzas morales, éticas o espirituales. El foco de la parábola es el punto central que capta la atención del receptor, mientras que la directriz es el mensaje o la enseñanza que se revela a través de la historia. Ambos elementos son fundamentales para que la parábola cumpla su propósito de enseñar y provocar la reflexión.
Movimiento de una parábola
La parábola es una curva que se forma cuando se lanza un objeto en el aire con un ángulo determinado. El movimiento de una parábola se puede describir utilizando ecuaciones matemáticas.
En el movimiento parabólico, las ecuaciones más importantes son la ecuación de la trayectoria y la ecuación de la altura máxima.
La ecuación de la trayectoria de una parábola se puede expresar como:
y = ax^2 + bx + c
Donde ‘y’ representa la altura, ‘x’ representa la distancia horizontal y ‘a’, ‘b’ y ‘c’ son constantes que dependen de las condiciones iniciales del movimiento.
La ecuación de la altura máxima se obtiene derivando la ecuación de la trayectoria y encontrando el valor de ‘x’ que hace que la derivada sea igual a cero. Este valor de ‘x’ corresponde al punto más alto de la parábola.
El movimiento de una parábola también está influenciado por la gravedad. La gravedad afecta la trayectoria del objeto, haciendo que la parábola sea más pronunciada y caiga más rápidamente hacia abajo.
En resumen, el movimiento de una parábola se puede describir utilizando ecuaciones matemáticas como la ecuación de la trayectoria y la ecuación de la altura máxima. Además, la gravedad juega un papel importante en la formación de la parábola y en su movimiento.
Interpretación de la parábola en diferentes contextos
La interpretación de la parábola puede variar dependiendo del contexto en el cual se analice.
Contexto religioso
En un contexto religioso, las parábolas suelen interpretarse como enseñanzas espirituales o morales. Son utilizadas para transmitir mensajes de fe, valores y principios religiosos. La parábola es una herramienta poderosa para transmitir conceptos abstractos de manera accesible y comprensible.
Contexto literario
Dentro de la literatura, las parábolas son consideradas como un género de narrativa breve que busca transmitir una enseñanza a través de una historia ficticia. Estas historias alegóricas son apreciadas por su capacidad de encapsular lecciones universales en un formato conciso y directo.
Contexto filosófico
En el ámbito filosófico, las parábolas son objeto de análisis y reflexión, donde se busca desentrañar el significado profundo de las metáforas utilizadas. Estas historias breves invitan a la reflexión y al cuestionamiento de las verdades establecidas.
Contexto educativo
En el contexto educativo, las parábolas son utilizadas como recursos didácticos para enseñar valores, principios éticos y lecciones de vida a través de ejemplos prácticos. La parábola enseña de forma tangible, permitiendo a los estudiantes relacionar la historia con su propia experiencia.
En conclusión, la interpretación de la parábola puede variar dependiendo del contexto en el que se analice, pero siempre es una poderosa herramienta para transmitir enseñanzas y reflexiones en diferentes ámbitos de la vida.