«`html
En el cálculo diferencial, la continuidad es un concepto fundamental que nos permite comprender el comportamiento de funciones en un punto específico o en un intervalo. Explorar la continuidad en estas dos situaciones nos proporciona una comprensión más profunda de cómo las funciones se comportan en diferentes contextos. En este artículo, analizaremos detalladamente la continuidad en un punto y en un intervalo, explorando ejemplos y casos particulares para ilustrar su importancia en el cálculo diferencial.
La continuidad en un punto y en un intervalo es un aspecto crucial en el estudio del cálculo diferencial, ya que nos permite entender la relación entre la función y su comportamiento local y global. Al comprender la continuidad en estas dos situaciones, somos capaces de abordar una amplia gama de problemas y aplicaciones en el ámbito matemático y científico. En este artículo, nos sumergiremos en el análisis detallado de la continuidad en un punto y en un intervalo, explorando sus implicaciones y su relevancia en el estudio del cálculo diferencial. ¡Acompáñanos en este viaje de exploración matemática!
«`
En el estudio del cálculo diferencial, la noción de continuidad en un punto desempeña un papel crucial. La importancia de la continuidad en un punto radica en su capacidad para proporcionar información detallada sobre el comportamiento de una función en una ubicación específica. Al comprender este concepto, somos capaces de analizar la suavidad y la estabilidad de la función en ese punto particular, lo que a su vez nos permite comprender su comportamiento local con mayor claridad.
La continuidad en un punto nos brinda información valiosa sobre la «fluidez» de una función en una ubicación puntual. Este concepto nos permite comprender cómo se comporta la función cerca del punto en términos de suavidad y conexiones sin rupturas. Esto resulta esencial en la comprensión del comportamiento local de la función, lo que a su vez tiene importantes implicaciones en una variedad de aplicaciones matemáticas y científicas.
Cuando exploramos la continuidad en un intervalo, nos adentramos en un análisis más amplio del comportamiento de la función en un rango de valores. La implicación de la continuidad en un intervalo radica en su capacidad para proporcionar información sobre la conexión y uniformidad de la función en un rango específico de valores. Al comprender este concepto, somos capaces de analizar la estabilidad y la coherencia de la función en ese intervalo, lo que a su vez nos permite comprender su comportamiento global con mayor claridad.
La continuidad en un intervalo nos brinda información valiosa sobre la «uniformidad» de una función en un rango de valores. Este concepto nos permite comprender cómo se comporta la función en términos de conexión y coherencia dentro de ese intervalo específico. Esto resulta esencial en la comprensión del comportamiento global de la función en un rango de valores, lo que tiene importantes implicaciones en la modelización matemática y en la solución de problemas del mundo real.
Al comprender la continuidad en un punto y en un intervalo, somos capaces de abordar una amplia gama de problemas y aplicaciones en el ámbito matemático y científico. El análisis detallado de estos dos aspectos de la continuidad nos permite comprender el comportamiento de las funciones en diferentes contextos, lo que a su vez nos proporciona herramientas poderosas para abordar problemas desafiantes en el cálculo diferencial.
En resumen, la exploración de la continuidad en un punto y en un intervalo en el cálculo diferencial nos brinda una comprensión más profunda de cómo las funciones se comportan en diferentes contextos. Al comprender la importancia y las implicaciones de la continuidad en estas dos situaciones, somos capaces de abordar una amplia gama de problemas y aplicaciones en el ámbito matemático y científico. En los siguientes apartados, analizaremos ejemplos concretos y casos particulares para ilustrar la importancia de la continuidad en un punto y en un intervalo en el estudio del cálculo diferencial, ¡así que mantente atento a nuestra exploración matemática!
Continuidad en un Punto y en un Intervalo: Definiciones Fundamentales
La continuidad en un punto y en un intervalo es un concepto central en el cálculo diferencial, y comprender sus definiciones fundamentales es crucial para adentrarnos en su estudio. En esta sección, exploraremos las definiciones clave que nos permitirán comprender la continuidad en estas dos situaciones.
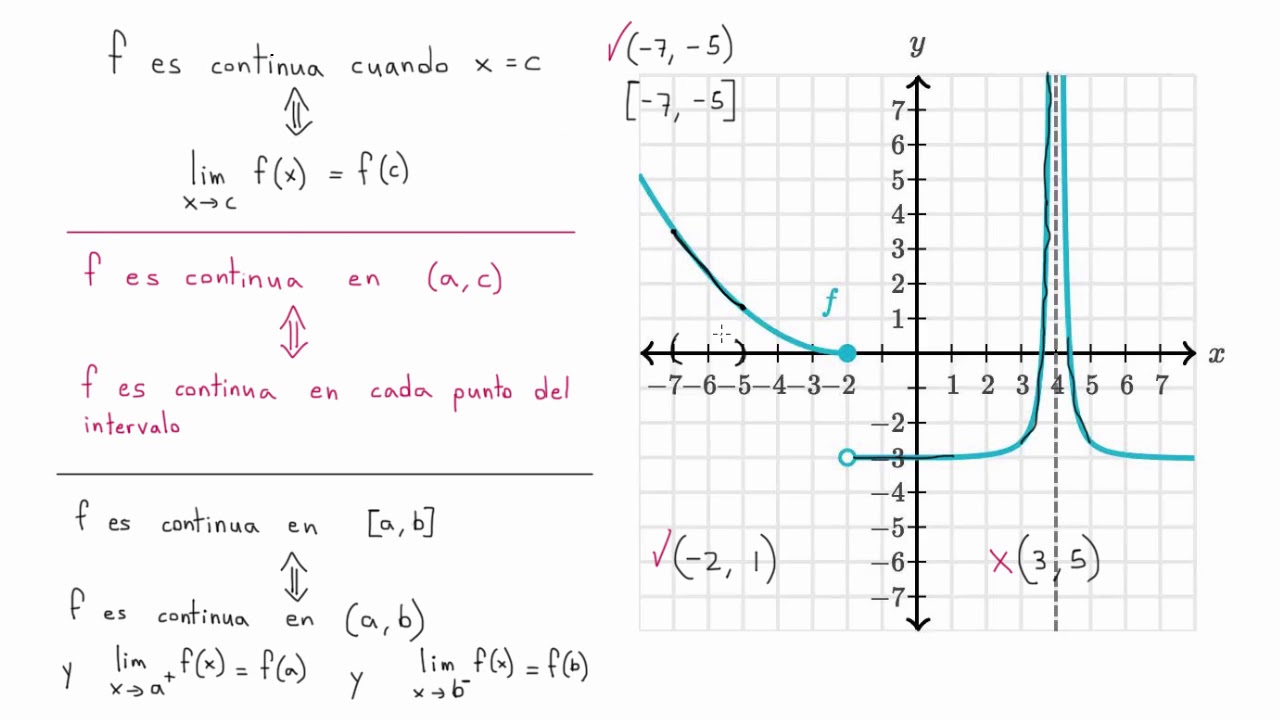
Definición de Continuidad en un Punto: En matemáticas, una función f se dice continua en un punto c si cumple con la condición de límite siguiente: lim(x->c) f(x) = f(c). Esta condición establece que el límite de la función cuando x tiende a c es igual al valor de la función en c, lo que implica que la función no presenta discontinuidades en ese punto.
Definición de Continuidad en un Intervalo: La continuidad de una función f en un intervalo [a, b] significa que la función está definida y continua para todos los valores de x en el intervalo [a, b]. Esto implica que la función no presenta saltos, agujeros ni brechas en ese intervalo.
Al comprender estas definiciones fundamentales, somos capaces de adentrarnos en el análisis más detallado de la continuidad en un punto y en un intervalo. A través de ejemplos y casos particulares, ilustraremos la relevancia y las implicaciones de estas definiciones en el estudio del cálculo diferencial.
Continuidad en un Punto: Ejemplos Prácticos
Para comprender mejor el concepto de continuidad en un punto, analicemos algunos ejemplos prácticos que nos ayudarán a visualizar su importancia en el cálculo diferencial.
Ejemplo 1: Consideremos la función f(x) = 2x + 3. Evaluemos la continuidad de esta función en el punto c = 2. Para que la función sea continua en c, el límite de la función cuando x tiende a 2 debe ser igual al valor de la función en 2.
lim(x->2) (2x + 3) = 2 * 2 + 3 = 7
f(2) = 2 * 2 + 3 = 7
Al observar que lim(x->2) (2x + 3) = f(2), podemos concluir que la función f(x) = 2x + 3 es continua en el punto c = 2.
Ejemplo 2: Ahora consideremos la función g(x) = 1/x. Evaluemos la continuidad de esta función en el punto c = 0. Para que la función sea continua en c, el límite de la función cuando x tiende a 0 debe ser igual al valor de la función en 0.
lim(x->0) (1/x) = DNE (Does Not Exist)
g(0) = 1/0 = DNE (Does Not Exist)
Al observar que el límite de la función cuando x tiende a 0 no existe, concluimos que la función g(x) = 1/x no es continua en el punto c = 0 debido a la discontinuidad causada por una asíntota vertical.
Al analizar estos ejemplos prácticos, podemos visualizar la importancia de la continuidad en un punto en el estudio del cálculo diferencial. La capacidad de evaluar la continuidad de una función en un punto específico nos proporciona herramientas poderosas para comprender su comportamiento local y suavidad en esa ubicación puntual.
Continuidad en un Intervalo: Casos Particulares
Al explorar la continuidad en un intervalo, nos encontramos con varios casos particulares que nos permiten comprender mejor cómo se comporta una función en un rango de valores. Analicemos algunos casos concretos que ilustrarán la relevancia de la continuidad en un intervalo en el cálculo diferencial.
Caso 1: Continuidad en un intervalo cerrado [a, b]
Consideremos una función f(x) definida en el intervalo cerrado [a, b]. Esta función será continua en el intervalo [a, b] si cumple con la condición de la continuidad para todos los valores de x en dicho intervalo. Esto implica que la función no presenta saltos, agujeros ni brechas en el intervalo completo.
Caso 2: Continuidad en un intervalo abierto (a, b)
Si una función f es continua en un intervalo abierto (a, b), esto significa que cumple con la condición de la continuidad para todos los valores de x en el intervalo a < x < b. Al no haber restricciones en los extremos del intervalo, la función debe mantener su suavidad y conexión a lo largo de todo el rango sin presentar discontinuidades.
Al analizar estos casos particulares, somos capaces de comprender la importancia de la continuidad en un intervalo en el cálculo diferencial. La capacidad de evaluar la continuidad de una función en un rango de valores nos proporciona herramientas poderosas para comprender su comportamiento global y uniformidad en ese intervalo específico.
Conclusiones y Aplicaciones Prácticas
En este artículo, hemos explorado detalladamente la continuidad en un punto y en un intervalo en el cálculo diferencial. Al comprender la importancia y las implicaciones de la continuidad en estas dos situaciones, somos capaces de abordar una amplia gama de problemas y aplicaciones en el ámbito matemático y científico.
La capacidad de evaluar la continuidad de una función en un punto específico nos proporciona herramientas poderosas para comprender su comportamiento local y suavidad en esa ubicación puntual. Del mismo modo, la capacidad de evaluar la continuidad de una función en un rango de valores nos proporciona herramientas poderosas para comprender su comportamiento global y uniformidad en ese intervalo específico.
En el estudio del cálculo diferencial, la continuidad en un punto y en un intervalo nos permite comprender el comportamiento de las funciones en diferentes contextos, lo que a su vez nos proporciona herramientas poderosas para abordar problemas desafiantes y aplicaciones del mundo real. Al explorar ejemplos concretos y casos particulares, hemos ilustrado la relevancia y la importancia de la continuidad en un punto y en un intervalo en el estudio del cálculo diferencial.
En resumen, la exploración detallada de la continuidad en un punto y en un intervalo nos brinda una comprensión más profunda de cómo las funciones se comportan en diferentes contextos. Este conocimiento resulta fundamental en el estudio del cálculo diferencial y tiene importantes implicaciones en la modelización matemática y en la solución de problemas del mundo real. ¡Acompáñanos en nuestro viaje de exploración matemática y descubramos juntos las maravillas de la continuidad en el cálculo diferencial!