¿Qué es la forma estándar centrada en el origen?
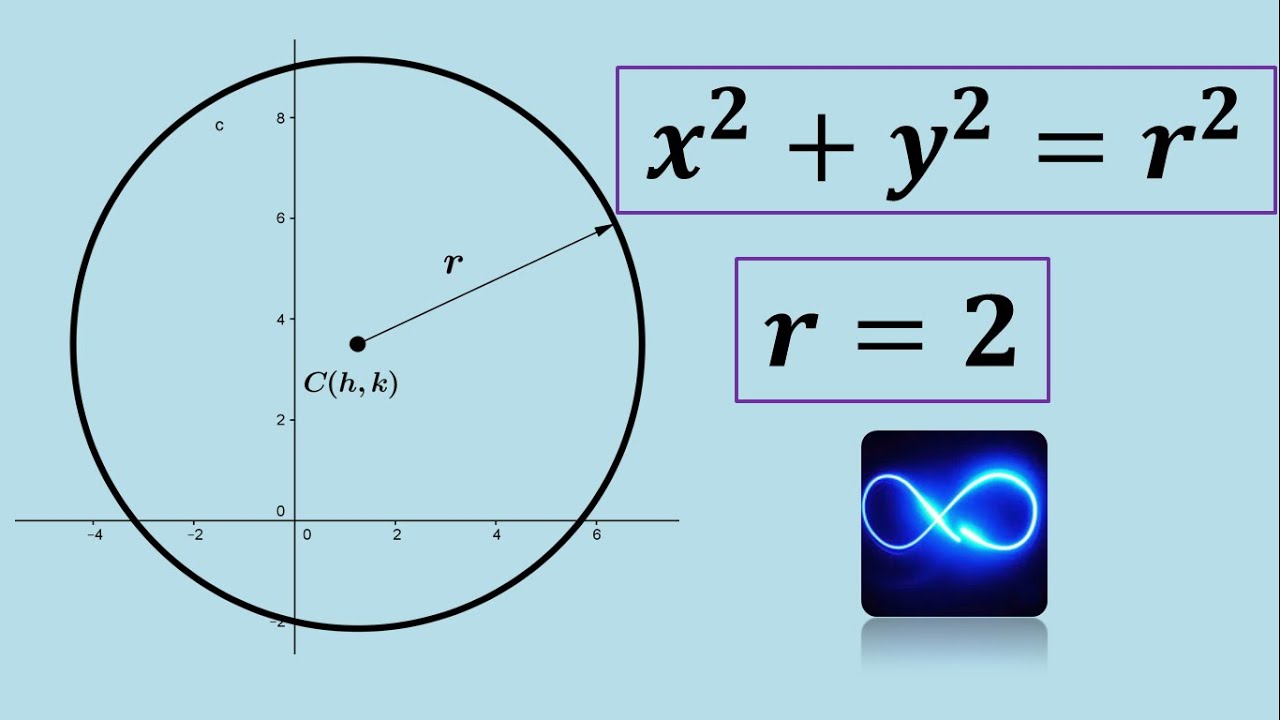
La forma estándar centrada en el origen es una técnica utilizada en matemáticas para representar las ecuaciones de una figura geométrica en un plano cartesiano. En esta forma, el centro de coordenadas (0,0) se encuentra en el centro de la figura y se utiliza para simplificar los cálculos.
En la forma estándar centrada en el origen, las ecuaciones de las figuras geométricas se expresan de manera más simple y simétrica. Por ejemplo, en la forma estándar de una circunferencia centrada en el origen, la ecuación sería x^2 + y^2 = r^2, donde x e y representan las coordenadas del punto en la circunferencia y r es el radio de la misma.
Esta forma de representación facilita el estudio y análisis de las figuras geométricas, ya que permite identificar de manera más clara las características principales de las mismas. Además, al tener el centro en el origen, se simplifican los cálculos de distancias y medidas relacionadas con la figura.
Es importante destacar que la forma estándar centrada en el origen es una de las muchas formas de representar las figuras geométricas en el plano cartesiano. Dependiendo de la situación o problema a resolver, puede ser más conveniente utilizar otras formas de representación.
En conclusión, la forma estándar centrada en el origen es una técnica utilizada en matemáticas para representar las ecuaciones de figuras geométricas en el plano cartesiano. Permite simplificar los cálculos y obtener una representación más clara de las características de la figura.
Pasos para determinar la forma estándar centrada en el origen
Paso 1: Determinar los coeficientes de la ecuación
Para determinar la forma estándar centrada en el origen de una ecuación, primero debes escribir la ecuación en su forma general: Ax + By + C = 0. Aquí, A, B y C son los coeficientes que necesitamos conocer.
Paso 2: Despejar la variable independiente
El siguiente paso es despejar la variable independiente (x) de la ecuación. Para hacer esto, debemos restar Ax de ambos lados de la ecuación, y luego dividir por B:
x = -A/B – Cy/B
Paso 3: Despejar la variable dependiente
Después de despejar x, necesitamos despejar la variable dependiente (y). Para hacer esto, debemos restar Cy/B de ambos lados de la ecuación:
y = -A/B – Cy/B
Paso 4: Factorizar los coeficientes
El siguiente paso es factorizar los coeficientes A, B y C, si es posible. Esto significa que debemos buscar los factores comunes en los coeficientes y dividirlos para simplificar la expresión.
Paso 5: Simplificar la ecuación
Una vez que hayamos factorizado los coeficientes, podemos simplificar la ecuación aún más. Esto implica reducir los términos semejantes y combinarlos para obtener una forma más simplificada de la ecuación.
Paso 6: Escribir la forma estándar centrada en el origen
Finalmente, podemos escribir la ecuación en su forma estándar centrada en el origen. Esta forma tendrá la siguiente estructura: (x – h)^2 + (y – k)^2 = r^2, donde (h, k) es el centro de la circunferencia y r es el radio.
¡Y eso es todo! Sigue estos pasos y podrás determinar la forma estándar centrada en el origen de cualquier ecuación.
Ejemplos de resolución de la forma estándar centrada en el origen
La forma estándar centrada en el origen es una forma comúnmente utilizada para representar ecuaciones lineales en el plano cartesiano. En esta forma, la ecuación de la recta se expresa como:
ax + by = c
Ejemplo 1:
Supongamos que queremos representar la recta que pasa por los puntos (2, 3) y (5, 1). Para resolverlo en forma estándar centrada en el origen, primero calculamos la pendiente:
m = (1 – 3) / (5 – 2) = -2/3
Ahora, utilizamos uno de los puntos y la pendiente en la fórmula general de la ecuación de la recta:
3 – (2)(-2/3) = c
Simplificando, obtenemos:
3 + 4/3 = c
c = 13/3
Por lo tanto, la ecuación de la recta que pasa por los puntos (2, 3) y (5, 1) en forma estándar centrada en el origen es:
2x/3 + y/3 = 13/3
Ejemplo 2:
Supongamos que tenemos la ecuación de la recta en su forma pendiente-intersección: y = 2x + 4. Para convertirlo a la forma estándar centrada en el origen, simplemente restamos 2x de ambos lados de la ecuación:
-2x + y = 4
Así, la ecuación de la recta en forma estándar centrada en el origen es:
-2x + y = 4
Estos son solo dos ejemplos que demuestran cómo resolver ecuaciones lineales en la forma estándar centrada en el origen. Es una forma útil y comúnmente utilizada para representar rectas en el plano cartesiano.
Aplicaciones de la forma estándar centrada en el origen
La forma estándar centrada en el origen es una ecuación algebraica que se utiliza comúnmente en matemáticas y ciencias para representar una variedad de situaciones y fenómenos. Aunque puede parecer complicada al principio, esta forma tiene muchas aplicaciones prácticas y es ampliamente utilizada por los científicos y los ingenieros en sus investigaciones y cálculos.
1. Geometría y Cálculo
En geometría, la forma estándar centrada en el origen se utiliza para describir figuras y determinar propiedades como simetría, intersecciones y áreas. También es de gran utilidad en el cálculo, ya que permite hallar las derivadas e integrales de las funciones de manera más sencilla y sistemática.
2. Física
En física, esta forma es esencial para el estudio de varios fenómenos naturales como el movimiento de los cuerpos, el comportamiento de las ondas y la ley de la gravitación universal. Además, permite modelar y predecir el comportamiento de sistemas complejos mediante ecuaciones diferenciales.
3. Economía y Finanzas
En economía y finanzas, la forma estándar centrada en el origen tiene aplicaciones en el análisis de los costos, la oferta y la demanda, así como en la determinación de precios y márgenes de beneficio. También se utiliza en la modelización de los mercados financieros y en la evaluación de inversiones.
4. Ingeniería y Ciencias de la Computación
En ingeniería y ciencias de la computación, esta forma es esencial para el diseño y análisis de sistemas, circuitos y algoritmos. Permite describir y solucionar problemas complejos de manera más estructurada y eficiente, facilitando la implementación de soluciones prácticas y precisas.
5. Estadística
En estadística, la forma estándar centrada en el origen se utiliza para representar y analizar datos de manera sistemática. Permite calcular parámetros estadísticos como la media, la desviación estándar y la correlación, y facilita la comparación y la interpretación de resultados.
En resumen, la forma estándar centrada en el origen tiene numerosas aplicaciones en distintas áreas del conocimiento. Su utilidad radica en su capacidad para simplificar y representar de manera eficiente fenómenos y situaciones complejas, lo cual resulta de gran beneficio para los científicos, los ingenieros y los profesionales en general.
Consejos para utilizar la forma estándar centrada en el origen correctamente
La forma estándar centrada en el origen es una herramienta fundamental en muchas ramas de la matemática y la física. Esta forma de representar ecuaciones y conceptos ayuda a simplificar cálculos y entender mejor los fenómenos. Aquí te ofrecemos algunos consejos para utilizar esta forma correctamente:
1. Comprende el concepto: Antes de utilizar la forma centrada en el origen, es importante entender qué significa y cómo se aplica. Investiga y estudia el concepto en detalle para asegurarte de que lo estás utilizando correctamente.
2. Utiliza las etiquetas : Para resaltar las frases más importantes del texto, puedes utilizar la etiqueta HTML . Por ejemplo, si quieres enfatizar la importancia de una fórmula o de un paso en un cálculo, puedes utilizar esta etiqueta.
3. Utiliza las etiquetas H3: Para dividir el texto en secciones y organizar tus ideas, puedes utilizar las etiquetas HTML H3. Estas te permitirán dar título a cada sección y darle estructura al texto.
4. Utiliza listas en HTML: Si deseas enumerar consejos o pasos a seguir, puedes utilizar listas en HTML. Esto ayudará a que tu texto sea más ordenado y fácil de seguir. Puedes utilizar las etiquetas
- (lista desordenada) o
- (lista ordenada) y dentro de ellas las etiquetas
- para cada elemento de la lista.
5. Usa negritas (): Además de la etiqueta , también puedes utilizar la etiqueta HTML para poner en negrita palabras o frases que desees resaltar aún más en el texto. Esto ayudará a que los lectores identifiquen fácilmente la información más relevante.
Recuerda siempre verificar que estás utilizando las etiquetas y elementos HTML de forma correcta y cerrar todas las etiquetas adecuadamente para evitar errores en tu documento.
Utilizar la forma estándar centrada en el origen correctamente puede ser una herramienta poderosa para resolver problemas matemáticos y físicos. Sigue estos consejos y práctica regularmente para mejorar tus habilidades en este campo. ¡Buena suerte!