La fórmula de la hiperbola centrada en el origen es una de las herramientas más importantes en la geometría analítica. Permite describir la forma y las propiedades de una hiperbola en un plano cartesiano. Comprender esta fórmula es crucial para estudiar y trabajar con hiperbolas en matemáticas y aplicaciones científicas y técnicas.
Definición de la hiperbola
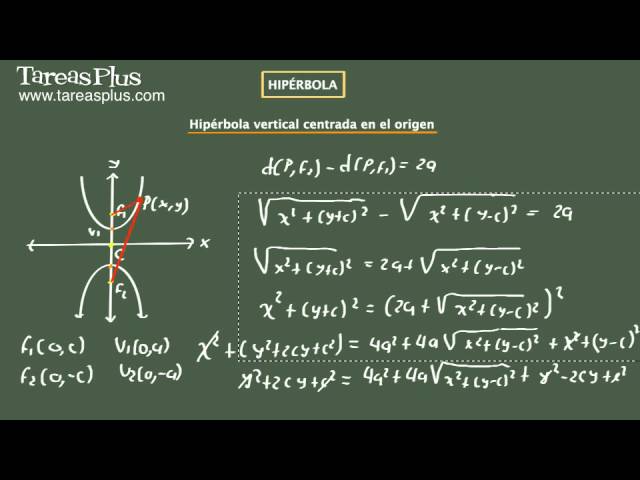
Antes de sumergirnos en la fórmula, es fundamental comprender qué es una hiperbola. En geometría, una hiperbola es el lugar geométrico de los puntos en un plano cuya diferencia de las distancias a dos puntos fijos, llamados focos, es constante. Esta forma geométrica es simétrica respecto a sus ejes y presenta propiedades únicas que la hacen intrigante y relevante en diferentes contextos matemáticos y físicos.
Fórmula general de la hiperbola centrada en el origen
La fórmula general de una hiperbola centrada en el origen tiene la forma:
[ frac{x^2}{a^2} – frac{y^2}{b^2} = 1 ]
donde ( a ) y ( b ) son constantes que determinan la apertura y la forma de la hiperbola. Esta ecuación proporciona información crucial sobre la posición de los vértices, fócos, asíntotas y otras características importantes de la hiperbola en el plano cartesiano.
Características de la fórmula
La fórmula general revela varias características clave de la hiperbola. La presencia de ( a^2 ) bajo el término ( x^2 ) determina la transversalidad de la hiperbola, mientras que ( b^2 ) bajo el término ( y^2 ) controla la conjugación. Estos parámetros definen la escala y la orientación de la hiperbola en el plano, lo que permite visualizar su forma y propiedades de manera precisa.
Vértices y focos de la hiperbola
Utilizando la fórmula, podemos identificar los vértices y los focos de la hiperbola. Los vértices de la hiperbola se encuentran en los puntos ( (pm a, 0) ), lo que nos permite trazar los ejes de la figura. Por otro lado, los focos se ubican en ( (pm c, 0) ), donde ( c ) está dado por la relación ( c^2 = a^2 + b^2 ). Estas ubicaciones son esenciales para comprender la distribución y el enfoque de la hiperbola en el plano cartesiano.
Asíntotas de la hiperbola
Otra característica fundamental de la hiperbola es la presencia de asíntotas, que son líneas rectas que la hiperbola parece acercarse indefinidamente a medida que se extiende hacia fuera. Las ecuaciones de las asíntotas de una hiperbola centrada en el origen toman la forma ( y = pm frac{b}{a}x ). Estas líneas imaginarias ayudan a visualizar el comportamiento de la hiperbola en regiones lejanas y son cruciales para comprender su comportamiento asintótico.
Ejemplos y aplicaciones
La fórmula de la hiperbola centrada en el origen tiene numerosas aplicaciones en matemáticas, física, ingeniería y otras disciplinas científicas. Desde el diseño de antenas de alta frecuencia hasta la modelización de órbitas planetarias, comprender y manipular hiperbolas es crucial para resolver problemas prácticos y teóricos en diversas áreas del conocimiento. Un ejemplo concreto es la predicción de trayectorias de naves espaciales y satélites, donde las hiperbolas ayudan a calcular los puntos de acercamiento máximo y la velocidad relativa en misiones espaciales.
Significado geométrico y físico
El significado geométrico y físico de la fórmula de la hiperbola es profundo y multidimensional. No solo representa una relación matemática, sino que también describe curvas en el espacio que tienen implicaciones prácticas y teóricas. Por ejemplo, en óptica, las hiperbolas aparecen en la formación de imágenes en espejos cóncavos y en la modelización de ondas electromagnéticas. Este rango diverso de aplicaciones ilustra la importancia de comprender la fórmula de la hiperbola y sus implicaciones en la realidad física y matemática.
En resumen, la fórmula de la hiperbola centrada en el origen es una poderosa herramienta matemática que permite describir y comprender las propiedades fundamentales de las hiperbolas en el plano cartesiano. Desde su geometría hasta sus aplicaciones en ingeniería y ciencias, esta fórmula proporciona una base sólida para explorar y utilizar las hiperbolas en diversos contextos teóricos y prácticos. Un entendimiento profundo de esta fórmula es esencial para estudiantes, investigadores y profesionales que buscan aprovechar el poder y la versatilidad de las hiperbolas en sus respectivos campos de estudio y trabajo.