Ecuación de posición final e inicial
La diferencia entre dos posiciones en un sistema de coordenadas es un concepto fundamental en la física y las matemáticas. Para calcular la diferencia entre la posición final y la posición inicial, se utiliza una fórmula que nos permite determinar la magnitud y dirección de dicho cambio. A continuación, explicaré detalladamente cómo utilizar esta fórmula y su importancia en diversos contextos.
Definición de posición inicial y posición final
Antes de adentrarnos en la fórmula para calcular la diferencia, es crucial comprender el significado de posición inicial y posición final. En el contexto de la cinemática, la posición inicial se refiere a la ubicación de un objeto en un instante de tiempo específico, mientras que la posición final representa la ubicación del mismo objeto en otro instante de tiempo posterior.
Representación gráfica de la diferencia de posición
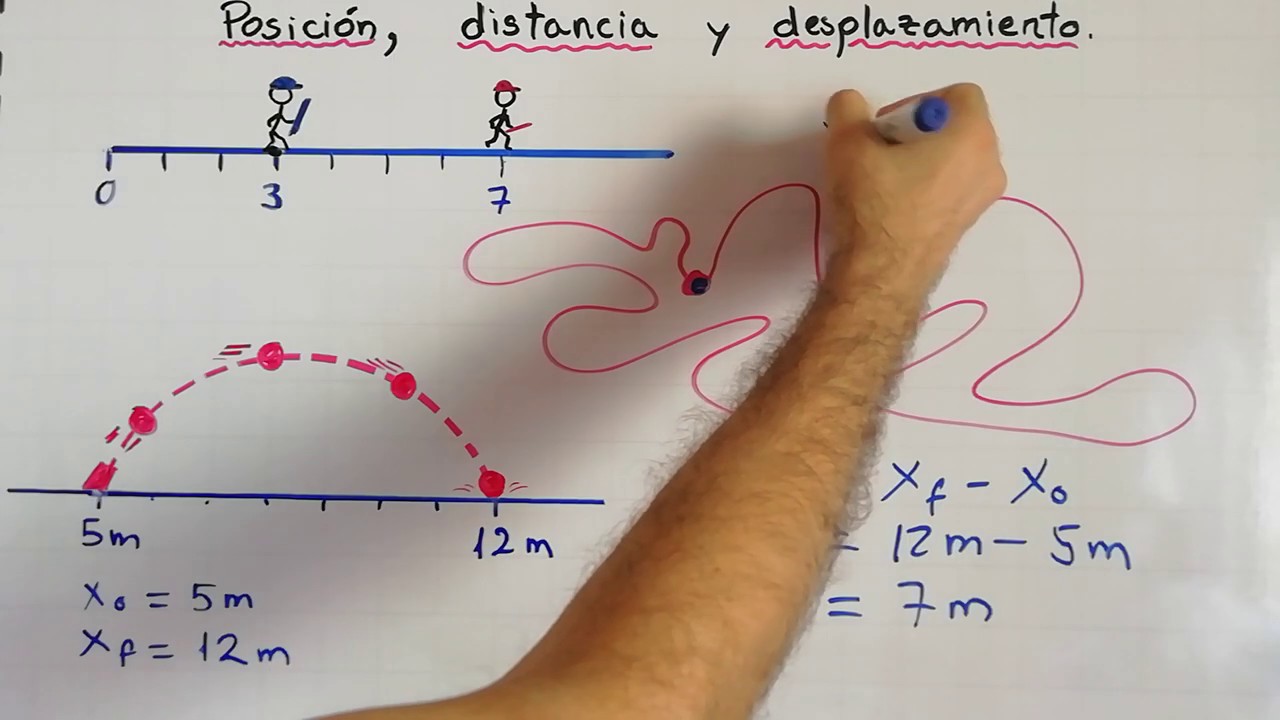
Visualizar la diferencia entre la posición final y la posición inicial puede facilitar la comprensión de su cálculo. Al representar las dos posiciones en un sistema de coordenadas, la diferencia se manifiesta como el vector que conecta ambos puntos. Esta visualización es crucial para entender la dirección y magnitud de la diferencia.
Fórmula para calcular la diferencia de posición
La fórmula utilizada para calcular la diferencia de posición entre dos puntos en un sistema de coordenadas es:
Diferencia = Posición final – Posición inicial
Esta fórmula toma en cuenta la dirección y magnitud del cambio entre las dos posiciones, permitiendo una descripción precisa de la variación espacial experimentada por un objeto o partícula.
Componentes de la fórmula
La fórmula de diferencia de posición tiene dos componentes fundamentales: la posición final y la posición inicial. Cada una de estas componentes representa un vector en el espacio tridimensional, permitiendo la representación completa de la diferencia en términos de dirección y magnitud.
Unidades de medida para la diferencia de posición
Al calcular la diferencia entre la posición final y la posición inicial, es crucial emplear unidades de medida coherentes con el sistema de coordenadas utilizado. Las unidades de longitud, como metros o kilómetros, son comúnmente empleadas en este contexto para expresar la magnitud de la diferencia en términos espaciales.
Importancia de la diferencia de posición en la física
La diferencia de posición es un concepto crucial en la física, ya que permite describir el desplazamiento de un objeto en el espacio. Esta magnitud vectorial es de gran importancia en el análisis de movimientos, trayectorias y cambios espaciales en diversos sistemas físicos.
Relación entre la diferencia de posición y la velocidad
La diferencia de posición está directamente relacionada con la velocidad de un objeto en movimiento. Al comprender la variación entre la posición final y la posición inicial, es posible determinar la velocidad instantánea o promedio del objeto en cuestión, lo que resulta fundamental en el análisis cinemático.
La fórmula para calcular la diferencia de posición es fundamental en la navegación y la geolocalización. En aplicaciones prácticas, como sistemas de posicionamiento global (GPS), la diferencia entre la posición actual y la posición previa se utiliza para determinar la trayectoria y la ubicación precisa de dispositivos móviles.
Utilización en el análisis de movimientos planetarios
En astronomía, la diferencia de posición entre cuerpos celestes es fundamental para el estudio de movimientos planetarios, eclipses y fenómenos astronómicos. El cálculo preciso de la variación de posición juega un papel crucial en la predicción y comprensión de eventos cósmicos.
Consideraciones en sistemas de coordenadas tridimensionales
En contextos tridimensionales, la fórmula para calcular la diferencia de posición se extiende para incluir los componentes en tres ejes ortogonales. La representación y cálculo preciso de la diferencia en sistemas tridimensionales es de vital importancia en campos como la ingeniería y la robótica.
Relación con la aceleración y la dinámica del movimiento
La diferencia de posición también está intrínsecamente relacionada con la aceleración y la dinámica del movimiento. Al conocer la variación espacial entre dos instantes de tiempo, es posible determinar la aceleración experimentada por un objeto en movimiento, lo que resulta crucial en el análisis de fuerzas y energía involucrada en el desplazamiento.
Importancia en la cinemática de partículas y cuerpos rígidos
En el estudio de la cinemática de partículas y cuerpos rígidos, la diferencia de posición es un elemento fundamental para la descripción de movimientos, trayectorias y velocidad. El análisis preciso de la variación espacial permite comprender el comportamiento cinemático de sistemas complejos en movimiento.
Aplicaciones en la ingeniería de control y la robótica móvil
En la ingeniería de control y la robótica móvil, el cálculo de la diferencia de posición es esencial para la planificación de trayectorias, el seguimiento de objetos móviles y la navegación autónoma. Esta herramienta matemática juega un papel crucial en sistemas automatizados que requieren precisión y fiabilidad en sus desplazamientos.
Consideraciones para sistemas de referencia no inerciales
En sistemas de referencia no inerciales, como aquellos en aceleración rotacional, la fórmula para calcular la diferencia de posición debe ser ajustada para tener en cuenta los efectos de la aceleración no inercial. Comprender la relación entre la diferencia de posición y la aceleración en estos contextos es esencial para el análisis preciso de movimientos en marcos de referencia acelerados.
En resumen, la fórmula para calcular la diferencia de posición entre la posición final y la posición inicial es una herramienta matemática fundamental en la descripción y análisis de movimientos, trayectorias y cambios espaciales en diversos contextos físicos y tecnológicos. Su aplicación abarca desde la física clásica hasta la ingeniería de control y la navegación satelital, siendo un componente esencial para comprender el comportamiento espacial de sistemas dinámicos. Entender con precisión esta fórmula permite a científicos, ingenieros y tecnólogos abordar con éxito una amplia variedad de problemas relacionados con el movimiento y la ubicación en el espacio tridimensional.