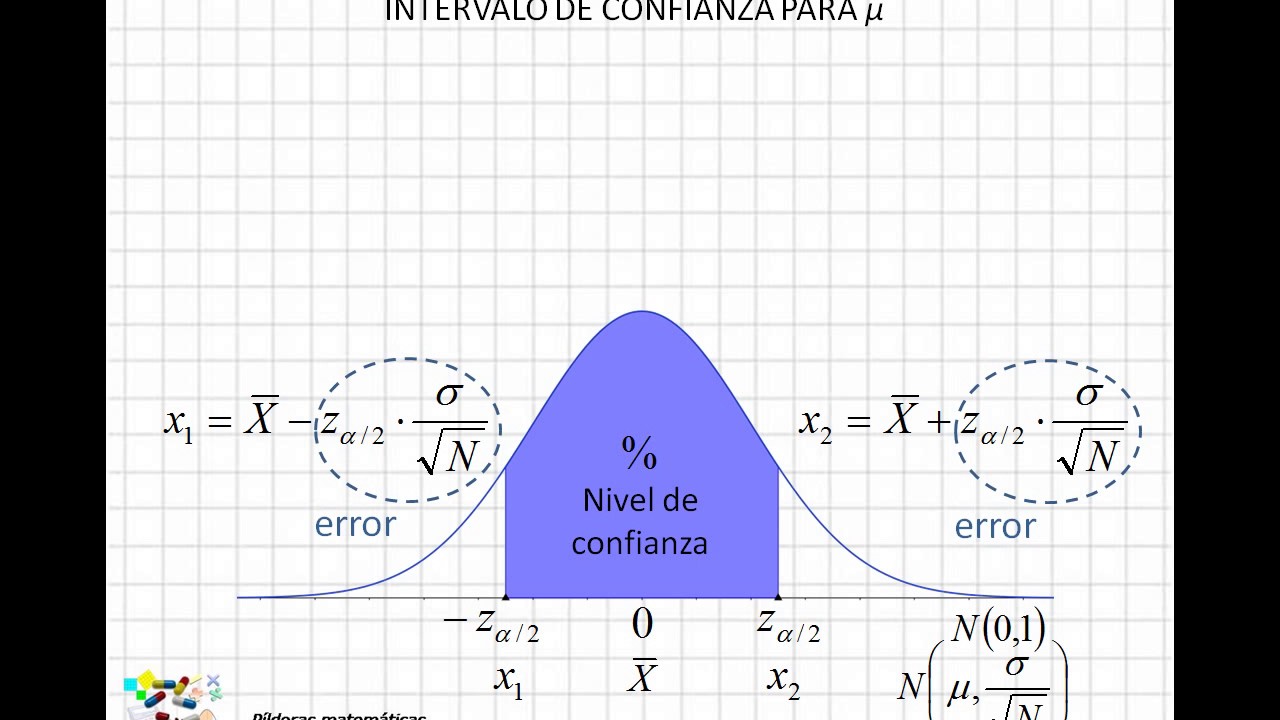
La generación de intervalos de confianza para la media de una población es un proceso fundamental en la estadística inferencial, que nos permite estimar con cierta certeza el rango en el que se encuentra la verdadera media poblacional. Esto es crucial en la toma de decisiones basadas en datos, ya que nos brinda información sobre la precisión de nuestras estimaciones.
Importancia de la precisión en la estimación
La precisión en la estimación de la media de una población es esencial para la toma de decisiones informadas. Cuando se trabaja con datos, es fundamental comprender cuán confiables son nuestras estimaciones y tener en cuenta la incertidumbre asociada a ellas. Los intervalos de confianza proporcionan una medida de esta incertidumbre y nos permiten evaluar la fiabilidad de nuestras conclusiones.
Al generar intervalos de confianza para la media poblacional, debemos considerar varios factores que afectan la precisión de nuestras estimaciones. Estos incluyen el tamaño de la muestra, el nivel de confianza deseado y la variabilidad de los datos. A continuación, exploraremos estos aspectos en detalle y cómo influyen en la generación de intervalos de confianza.
Tamaño de la muestra
El tamaño de la muestra desempeña un papel crucial en la generación de intervalos de confianza. A medida que el tamaño de la muestra aumenta, la precisión de nuestras estimaciones tiende a mejorar. Esto se debe a que una muestra más grande proporciona más información sobre la distribución de los datos y reduce la incertidumbre en torno a la estimación de la media poblacional.
Es importante tener en cuenta que un tamaño de muestra insuficiente puede llevar a intervalos de confianza demasiado amplios, lo que resulta en una estimación menos precisa de la media poblacional. Por lo tanto, al diseñar estudios o análisis de datos, es crucial considerar el tamaño de la muestra necesario para alcanzar el nivel de precisión deseado en la estimación de la media.
Nivel de confianza
El nivel de confianza especifica la probabilidad de que un intervalo de confianza capture la verdadera media poblacional. Comúnmente, se utiliza un nivel de confianza del 95%, lo que significa que si repitiéramos el proceso de muestreo y generación del intervalo de confianza muchas veces, esperaríamos que alrededor del 95% de los intervalos capturaran la verdadera media poblacional.
Al aumentar el nivel de confianza, el intervalo de confianza tiende a ser más amplio, lo que refleja una mayor certeza en la estimación. Por otro lado, al disminuir el nivel de confianza, el intervalo tiende a estrecharse, lo que indica una menor certeza en la estimación. Es fundamental comprender la relación entre el nivel de confianza y la precisión de las estimaciones al generar intervalos de confianza para la media de una población.
Variabilidad de los datos
La variabilidad de los datos influye significativamente en la generación de intervalos de confianza. Cuando los datos son altamente variables, es más probable que los intervalos de confianza sean más amplios, lo que refleja la incertidumbre en torno a la estimación de la media poblacional. Por otro lado, datos menos variables tienden a conducir a intervalos de confianza más estrechos, lo que indica una mayor certeza en las estimaciones.
Es crucial considerar la variabilidad de los datos al interpretar intervalos de confianza para la media de una población. Los datos altamente variables pueden requerir tamaños de muestra más grandes para lograr el mismo nivel de precisión que datos menos variables. Además, al comprender la variabilidad de los datos, podemos evaluar el grado de incertidumbre asociado a nuestras estimaciones y tomar decisiones informadas en consecuencia.
Proceso de generación de intervalos de confianza
Ahora que hemos explorado los factores que influyen en la generación de intervalos de confianza, es importante comprender el proceso paso a paso para estimar el intervalo de confianza para la media de una población.
Calcular la media muestral
El primer paso en el proceso es calcular la media de la muestra, que nos proporciona una estimación puntual de la media poblacional. Esta media muestral servirá como punto de partida para la construcción del intervalo de confianza.
Determinar el error estándar
El error estándar es una medida de la precisión de la estimación de la media muestral y está influenciado por el tamaño de la muestra y la variabilidad de los datos. Cuanto menor sea el error estándar, mayor será la precisión de la estimación de la media poblacional.
Seleccionar el nivel de confianza
El siguiente paso es seleccionar el nivel de confianza deseado para el intervalo. Comúnmente, se utiliza un nivel de confianza del 95%, pero este valor puede ajustarse según el grado de certeza requerido en la estimación.
Calcular el margen de error
El margen de error se calcula utilizando el error estándar y el valor crítico correspondiente al nivel de confianza seleccionado. Este margen de error nos indica el rango en el que esperamos que se encuentre la verdadera media poblacional.
Construir el intervalo de confianza
Finalmente, utilizando la media muestral y el margen de error, construimos el intervalo de confianza que estima el rango en el que la verdadera media poblacional se encuentra con cierta certeza, de acuerdo con el nivel de confianza seleccionado.
Aplicaciones de los intervalos de confianza
Los intervalos de confianza para la media de una población tienen numerosas aplicaciones en la investigación y la toma de decisiones. Algunas de las áreas en las que se utilizan con frecuencia incluyen:
Análisis de encuestas y estudios de opinión
Al realizar encuestas o estudios de opinión, es fundamental estimar la media de la población y proporcionar un intervalo de confianza que refleje la incertidumbre asociada a esta estimación. Los intervalos de confianza permiten a los investigadores y encuestadores comunicar la variabilidad en sus estimaciones y brindar una medida de su fiabilidad.
Estudios clínicos y de salud pública
En el campo de la medicina y la salud pública, la estimación precisa de la media de la población es crucial para la toma de decisiones clínicas y políticas. Los intervalos de confianza proporcionan información sobre la precisión de estas estimaciones, lo que es fundamental al evaluar el impacto de intervenciones médicas o políticas de salud pública.
Análisis financiero y económico
En el ámbito financiero y económico, la generación de intervalos de confianza para la media de una población es fundamental para evaluar la variabilidad en los datos financieros y económicos. Esto es esencial al tomar decisiones de inversión o diseñar políticas económicas basadas en datos.
La generación de intervalos de confianza para la media de una población es un proceso fundamental en la estadística inferencial que proporciona una medida de la incertidumbre asociada a nuestras estimaciones. Comprender los factores que influyen en la precisión de estos intervalos y el proceso paso a paso para su generación es crucial para la toma de decisiones informada basada en datos.
Al aplicar correctamente los principios de generación de intervalos de confianza, podemos estimar con confianza la media de una población y comunicar la fiabilidad de nuestras estimaciones en una variedad de contextos, desde la investigación científica hasta la toma de decisiones en el mundo real.