en HTML para el artículo:
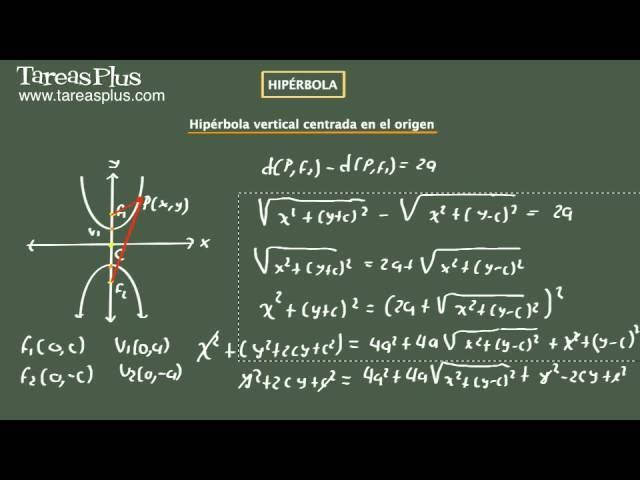
1. ¿Qué es una hipérbola vertical centrada en el origen?
Una hipérbola vertical centrada en el origen es una curva que se forma al intersectar un cono circular recto con un plano que corta ambas mitades del cono. A diferencia de una elipse, que tiene una forma ovalada, una hipérbola tiene una forma más abierta y asimétrica.
2. Ecuación de una hipérbola vertical centrada en el origen
Una hipérbola es una curva que se encuentra en el plano cartesiano. La ecuación general de una hipérbola vertical centrada en el origen es:
x^2/a^2 – y^2/b^2 = 1
Donde a y b son las longitudes de los ejes, y representan la distancia del centro de la hipérbola a los vértices.
En esta ecuación, el término x^2/a^2 está asociado al eje horizontal (paralelo al eje x), mientras que el término y^2/b^2 está asociado al eje vertical (paralelo al eje y).
La distancia focal de una hipérbola vertical centrada en el origen se puede calcular con la fórmula:
c = √(a^2 + b^2)
Donde c representa la distancia del centro de la hipérbola a las asíntotas.
La ecuación de las asíntotas de una hipérbola vertical centrada en el origen es:
- y = (b/a)x
- y = -(b/a)x
Estas asíntotas son rectas que se acercan infinitamente a la curva de la hipérbola.
3. Propiedades de una hipérbola vertical centrada en el origen
Las propiedades de una hipérbola vertical centrada en el origen son las siguientes:
1. Ecuación:
La ecuación general de una hipérbola vertical centrada en el origen es:
x2/a2 – y2/b2 = 1
donde a y b son las distancias desde el centro de la hipérbola hasta los vértices y el foco, respectivamente.
2. Ejes:
El eje mayor es la distancia entre los vértices de la hipérbola y tiene longitud 2a. El eje menor es la distancia entre las asíntotas de la hipérbola y tiene longitud 2b.
3. Vértices:
Los vértices de la hipérbola se encuentran en los puntos (a, 0) y (-a, 0).
4. Focos:
Los focos de la hipérbola se encuentran en los puntos (c, 0) y (-c, 0), donde c = √(a2 + b2).
5. Asíntotas:
Las asíntotas de la hipérbola son dos rectas que pasan por el centro de la hipérbola. Sus ecuaciones son:
y = (b/a)x y y = -(b/a)x
6. Distancias:
La distancia desde cualquier punto de la hipérbola hasta un foco más cercano es siempre igual a la distancia desde ese punto hasta la recta directriz, y esta distancia está dada por la fórmula d = |x ± a| / e, donde e = c / a es la excentricidad.
En resumen, una hipérbola vertical centrada en el origen se caracteriza por su ecuación general, la longitud de sus ejes, la ubicación de sus vértices y focos, las ecuaciones de sus asíntotas y las propiedades de las distancias entre los puntos de la hipérbola y los focos o la recta directriz.
4. Graficando una hipérbola vertical centrada en el origen
En esta entrada vamos a aprender cómo graficar una hipérbola vertical centrada en el origen utilizando HTML. Una hipérbola es una curva que se forma al cortar un cono con un plano inclinado.
Para graficar una hipérbola, necesitamos los valores de los parámetros a y b. El parámetro a representa la distancia desde el centro de la hipérbola hasta sus vértices, mientras que el parámetro b representa la distancia desde el centro hasta sus asíntotas.
La ecuación para una hipérbola vertical centrada en el origen es:
x2/a2 – y2/b2 = 1
Para empezar a graficar, podemos tomar los siguientes pasos:
- Calcula los valores de a y b.
- Crea un conjunto de puntos (x, y) que satisfagan la ecuación de la hipérbola.
- Dibuja la hipérbola conectando estos puntos.
- Agrega las asíntotas si es necesario.
Una vez que tengamos los valores de a y b, podemos encontrar el conjunto de puntos (x, y) que satisfacen la ecuación de la hipérbola. Para ello, podemos seleccionar varios valores de x, sustituirlos en la ecuación y resolver para y. Repitiendo este proceso, obtendremos una serie de puntos que podemos trazar en el plano.
Finalmente, debemos tener en cuenta las asíntotas de la hipérbola. Las asíntotas son líneas rectas que limitan la curva de la hipérbola. Para graficarlas, podemos calcular los valores de las líneas usando las siguientes fórmulas:
y = ±b/a * x
Estas líneas se dibujan en el plano conectando los puntos calculados.
Con estos pasos, hemos aprendido cómo graficar una hipérbola vertical centrada en el origen utilizando HTML. Espero que esta entrada te haya sido útil y te haya ayudado a comprender mejor este concepto.
5. Aplicaciones de la hipérbola vertical centrada en el origen
La hipérbola es una curva que tiene varias aplicaciones en diferentes campos, tanto en matemáticas como en la vida cotidiana. En esta ocasión, nos enfocaremos en las aplicaciones de la hipérbola vertical centrada en el origen.
5.1 Comunicaciones y tecnología
Las hipérbolas tienen aplicaciones en el diseño de antenas y en la transmisión de señales en telecomunicaciones. Las antenas parabólicas utilizadas en la recepción de señales satelitales suelen tener una forma similar a una hipérbola para optimizar la captación de la señal. Además, las propiedades reflectoras de la hipérbola también se utilizan en los diseños de antenas de radar.
5.2 Óptica
En óptica, las hipérbolas se utilizan en la construcción y diseño de espejos y lentes. Los espejos hipérbolicos son utilizados en telescopios y otros sistemas ópticos debido a sus propiedades de enfoque y amplificación de la luz. Asimismo, las lentes hipérbolicas son utilizadas en la fabricación de lentes de contacto y en óptica adaptativa.
5.3 Ingeniería y arquitectura
En ingeniería civil y arquitectura, las hipérbolas se utilizan para el diseño de puentes, especialmente para la forma de los arcos y las estructuras de soporte. Las hipérbolas también se utilizan en el diseño de rieles de tren, permitiendo trazados más suaves y eficientes.
5.4 Astronomía
En astronomía, las hipérbolas se utilizan para calcular trayectorias de objetos celestes, como cometas y asteroides. La órbita de estos cuerpos suele ser descrita por una hipérbola, lo que permite predecir su movimiento y trayectoria en el espacio.
Estas son solo algunas de las aplicaciones de la hipérbola vertical centrada en el origen. Esta curva tiene numerosos usos en diversos campos, demostrando su importancia y utilidad en diferentes áreas de estudio y práctica.