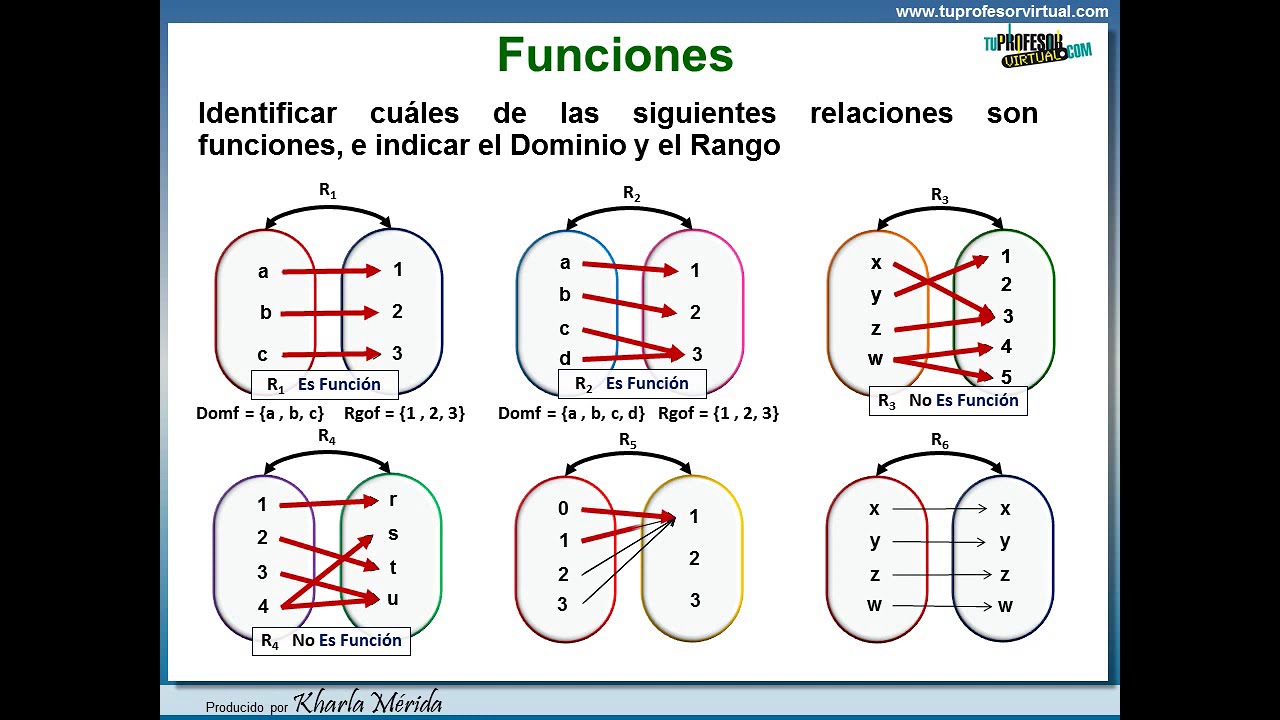
Al estudiar matemáticas, una de las áreas que a menudo genera confusión es la comprensión de relaciones y funciones. Es crucial entender la distinción entre estos conceptos, ya que pueden tener un impacto significativo en la resolución de problemas matemáticos. En esta guía, exploraremos cómo identificar cuál de estas relaciones es una función y desglosaremos los pasos para hacerlo de manera efectiva.
Antes de sumergirnos en los detalles, es esencial comprender la importancia de discernir entre una relación y una función en el contexto matemático. Este conocimiento proporciona una base sólida para abordar problemas más complejos y despeja el camino para un razonamiento matemático consistente y preciso.
Entendiendo las relaciones y funciones
Las relaciones y las funciones son conceptos fundamentales en matemáticas. Una relación entre dos conjuntos es simplemente un conjunto de pares ordenados que establecen una conexión entre los elementos de los conjuntos. Por otro lado, una función es un tipo específico de relación en la que cada elemento del primer conjunto está relacionado con exactamente un elemento del segundo conjunto. Este aspecto crucial de unicidad distingue a las funciones de las relaciones generales, y es la piedra angular para identificar si una relación dada es una función.
Diferenciando entre relaciones y funciones
La distinción fundamental entre una relación y una función radica en la asociación de cada elemento del dominio con exactamente un elemento del codominio. Mientras que una relación puede tener múltiples valores de salida para un solo valor de entrada, una función asigna cada valor único del dominio a un solo valor en el codominio. Este principio es esencial para determinar si una relación puede considerarse una función.
Identificando una función: los pasos clave
Para identificar si una relación dada es una función, es crucial seguir un enfoque sistemático que permita examinar la unicidad de la asociación entre los conjuntos. A continuación, se presentan los pasos clave para llevar a cabo este proceso con precisión y confianza.
Paso 1: Revisar las parejas ordenadas
El primer paso es analizar las parejas ordenadas que definen la relación. Una relación se representa como un conjunto de pares ordenados, donde el primer elemento de cada par es el valor de entrada, y el segundo elemento es el valor de salida. Al revisar estas parejas ordenadas, observa si un valor de entrada está asociado con más de un valor de salida. Si un valor de entrada tiene múltiples valores de salida, la relación no cumple con el criterio de unicidad y, por lo tanto, no es una función.
Paso 2: Verificar la unicidad
Una vez revisadas las parejas ordenadas, es importante verificar que cada valor de entrada esté asociado con un único valor de salida. Si cada elemento del dominio se relaciona con exactamente un elemento del codominio, la relación cumple con el requisito fundamental de una función. Este paso es crucial para confirmar que la relación en cuestión puede considerarse efectivamente como una función.
Paso 3: Graficar la relación
Una forma visualmente impactante de analizar si una relación es una función es mediante su representación gráfica. Si la relación se puede graficar como una función, esto proporciona una verificación adicional de su naturaleza funcional. Al trazar la relación en un plano cartesiano, observa si para cada valor de x hay un solo valor correspondiente de y. De esta manera, la representación gráfica puede brindar una perspectiva adicional sobre la unicidad de la relación.
Aplicando el concepto a situaciones reales
Una comprensión sólida de cómo identificar una función es fundamental, ya que se aplica a numerosos contextos en la vida cotidiana y en disciplinas más allá de las matemáticas. Desde la interpretación de datos científicos hasta la resolución de problemas de ingeniería, la habilidad para reconocer funciones es un componente esencial en el análisis y la toma de decisiones informadas.
Importancia en la resolución de problemas
En el ámbito de la ciencia y la ingeniería, la identificación de relaciones funcionales es esencial para comprender fenómenos naturales y modelar sistemas complejos. La capacidad de discernir entre una función y una relación general permite a los profesionales realizar predicciones precisas y extraer conclusiones significativas a partir de conjuntos de datos y observaciones empíricas.
Aplicaciones en el análisis de tendencias
En campos como la economía y la sociología, el concepto de funciones desempeña un papel crucial en el análisis de tendencias y proyecciones futuras. Al identificar funciones que modelan el comportamiento de variables, se pueden realizar predicciones informadas que respalden la toma de decisiones estratégicas y la planificación a largo plazo.
Conclusiones
En resumen, la capacidad para identificar cuál de estas relaciones es una función es un habilidad fundamental en matemáticas y tiene aplicaciones extendidas en diversas disciplinas. Al comprender la distinción clave entre relaciones y funciones, así como seguir un enfoque sistemático para identificar funciones, los estudiantes y profesionales pueden desarrollar una comprensión sólida de este concepto fundamental. Este conocimiento se traduce en la capacidad para abordar problemas matemáticos con claridad y precisión, así como para aplicar el concepto de funciones en contextos del mundo real, desde la ciencia hasta la toma de decisiones estratégicas.