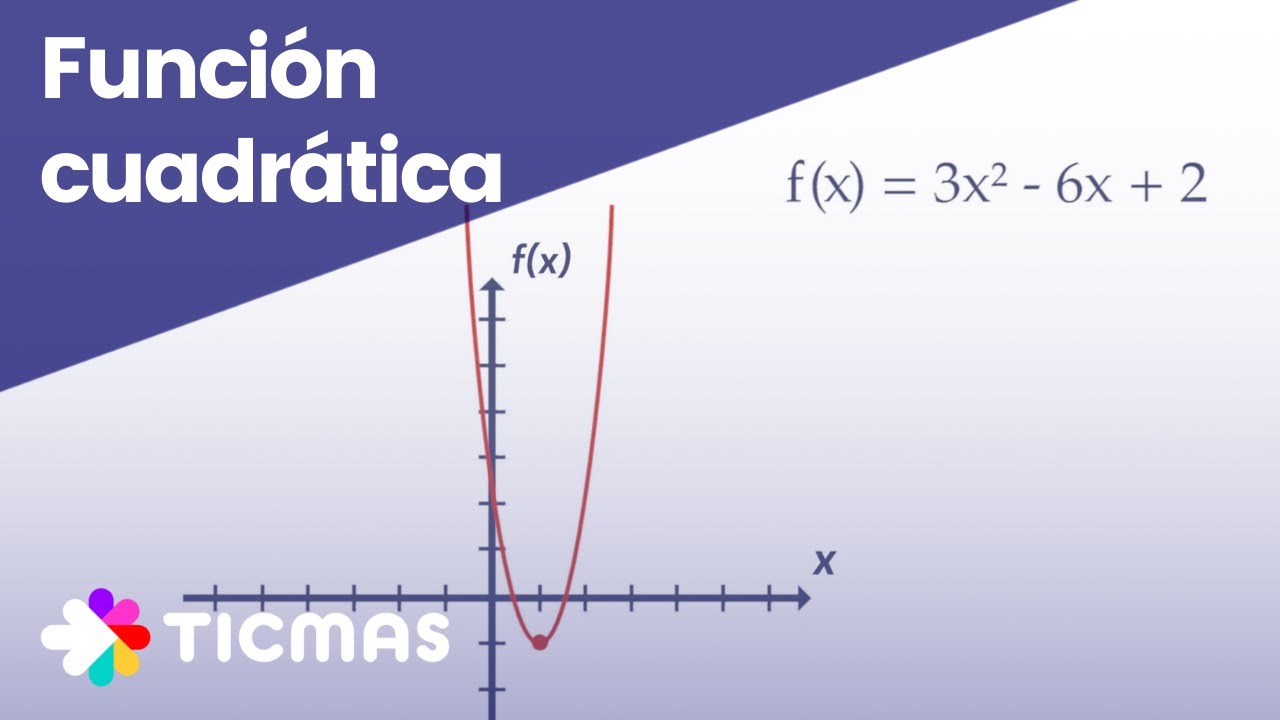
1. La forma general de una función cuadrática
La forma general de una función cuadrática es una ecuación de la forma:
f(x) = ax^2 + bx + c
Donde:
- a: es el coeficiente principal y determina si la parábola abre hacia arriba (si a > 0) o hacia abajo (si a < 0).
- b: es el coeficiente lineal y determina el desplazamiento horizontal de la parábola.
- c: es el término independiente y determina el desplazamiento vertical de la parábola.
- x: es la variable independiente.
- f(x): es la imagen de la variable x.
En esta forma general, podemos identificar claramente los componentes principales de la función cuadrática. Utilizando esta ecuación, podemos trazar el gráfico de la función y analizar su comportamiento.
2. El vértice de la parábola
En el estudio de las parábolas, una de las características más importantes es el vértice. El vértice de una parábola se define como el punto en el que la curva alcanza su punto máximo o mínimo, dependiendo de si se trata de una parábola hacia arriba (concavidad hacia arriba) o hacia abajo (concavidad hacia abajo).
El vértice de una parábola se encuentra en el punto de intersección entre el eje de simetría y la propia curva. El eje de simetría es una línea vertical que divide a la parábola en dos mitades reflejadas. Por lo tanto, el vertice se encuentra en la mitad de la parábola.
Para encontrar las coordenadas del vértice, se puede utilizar la fórmula general de la parábola, que es:
y = ax^2 + bx + c
Donde ‘a’, ‘b’ y ‘c’ son coeficientes que determinan la forma y posición de la parábola. Las coordenadas del vértice se calculan utilizando las siguientes fórmulas:
- x = -b / (2a)
- y = f(x) = a(x^2) + bx + c
La fórmula del valor de x permite encontrar la abscisa del vértice, es decir, su posición en el eje horizontal. Luego, sustituyendo ese valor de x en la ecuación original, se obtiene la ordenada del vértice, es decir, su posición en el eje vertical.
En resumen, el vértice de una parábola es un punto fundamental que nos brinda información sobre su forma y posición. Su cálculo se realiza utilizando las fórmulas correspondientes y es indispensable para el estudio detallado de estas curvas.
3. El eje de simetría
El eje de simetría es una línea imaginaria que divide una figura o un objeto en dos partes iguales y simétricas.
En matemáticas, el eje de simetría se utiliza para describir la simetría de una función o una ecuación. En una función, el eje de simetría es una línea vertical que divide el gráfico de la función en dos partes simétricas.
En la geometría, el eje de simetría puede ser horizontal, vertical o diagonal, dependiendo de la forma o el objeto. Por ejemplo, en un triángulo equilátero, el eje de simetría es una línea vertical que pasa por el vértice superior y divide el triángulo en dos partes simétricas.
El eje de simetría es una propiedad importante en el arte y el diseño. Muchas obras de arte y diseños tienen una simetría perfecta a lo largo de un eje, lo que les da un aspecto equilibrado y armonioso.
¿Cómo encontrar el eje de simetría en una figura?
Para encontrar el eje de simetría en una figura, es necesario identificar los puntos o líneas que dividen la figura en dos partes iguales.
En algunas figuras, como los cuadrados y los rectángulos, el eje de simetría es fácil de identificar, ya que pasa por el centro de la figura. En otras figuras, como los círculos y los triángulos equiláteros, el eje de simetría puede ser más difícil de encontrar, pero es posible identificarlo si se analiza la forma de la figura.
Al identificar el eje de simetría en una figura, es posible realizar transformaciones geométricas, como reflejar la figura a lo largo del eje de simetría, lo que crea una figura idéntica pero invertida.
Importancia del eje de simetría
El eje de simetría es una herramienta importante en la geometría y el diseño. Permite crear figuras y diseños equilibrados y armoniosos, lo que resulta atractivo visualmente. Además, el eje de simetría es utilizado en matemáticas para simplificar la resolución de ecuaciones y funciones.
En resumen, el eje de simetría es una línea imaginaria que divide una figura en dos partes iguales y simétricas. Es una propiedad importante en la geometría, el arte y el diseño.
4. Los puntos de intersección con los ejes
En el estudio de las funciones y las gráficas, uno de los conceptos fundamentales son los puntos de intersección con los ejes. Los ejes de coordenadas, formados por el eje x y el eje y, nos permiten ubicar puntos en el plano cartesiano.
Un punto de intersección con el eje x es aquel en el cual la gráfica de una función o una curva corta a dicho eje. Este punto se encuentra en la coordenada (x, 0). Es decir, su coordenada y es igual a cero. En términos matemáticos podemos representarlo como (x, 0).
Por otro lado, un punto de intersección con el eje y es aquel en el cual la gráfica de una función o una curva corta al eje y. Este punto se encuentra en la coordenada (0, y). Es decir, su coordenada x es igual a cero. Podemos representarlo matemáticamente como (0, y).
Es importante destacar que las funciones pueden tener más de un punto de intersección con los ejes, o incluso ninguno. Esto dependerá de las características de la función en cuestión. Por ejemplo, una función lineal siempre cortará al eje x en un único punto, pero puede no cortar al eje y en ningún punto si su pendiente es igual a cero.
Cabe mencionar también que es posible tener puntos de intersección con los ejes en funciones no lineales. En estos casos, la ubicación de dichos puntos dependerá de la forma de la curva y de los valores de los parámetros de la función.
Ejemplos de puntos de intersección con los ejes
Para ilustrar lo anteriormente expuesto, veamos algunos ejemplos:
- La función lineal y = 2x + 3 corta al eje x en el punto (0, 3) y no corta al eje y.
- La función cuadrática y = x^2 – 4 corta al eje x en los puntos (-2, 0) y (2, 0), y corta al eje y en el punto (0, -4).
- La función exponencial y = 2^x no corta al eje x, pero corta al eje y en el punto (0, 1).
Estos ejemplos nos muestran que es posible tener distintos puntos de intersección con los ejes dependiendo de la función en estudio.
5. La concavidad de la parábola
La concavidad de la parábola es un concepto fundamental en el estudio de las funciones cuadráticas. Nos permite determinar si la parábola se abre hacia arriba o hacia abajo.
Para entender la concavidad de una parábola, es necesario analizar el coeficiente principal de la función cuadrática. Si el coeficiente es positivo, entonces la parábola se abre hacia arriba. Por ejemplo, la función f(x) = 2x^2 tiene un coeficiente principal positivo y, por lo tanto, su concavidad es hacia arriba.
Por otro lado, si el coeficiente principal es negativo, la parábola se abre hacia abajo. Por ejemplo, la función g(x) = -3x^2 tiene un coeficiente principal negativo y, por lo tanto, su concavidad es hacia abajo.
Es importante destacar que la concavidad de la parábola también se puede determinar analizando el valor del discriminante de la función cuadrática. Si el discriminante es positivo, la parábola tendrá intersecciones con el eje x y, por lo tanto, su concavidad será hacia arriba. Por el contrario, si el discriminante es negativo, la parábola no tendrá intersecciones con el eje x y su concavidad será hacia abajo.
En resumen, la concavidad de una parábola se determina mediante el análisis del coeficiente principal o del discriminante de la función cuadrática. Estos análisis nos permiten identificar si la parábola se abre hacia arriba o hacia abajo, lo cual es fundamental para comprender su comportamiento y graficarla de manera precisa.