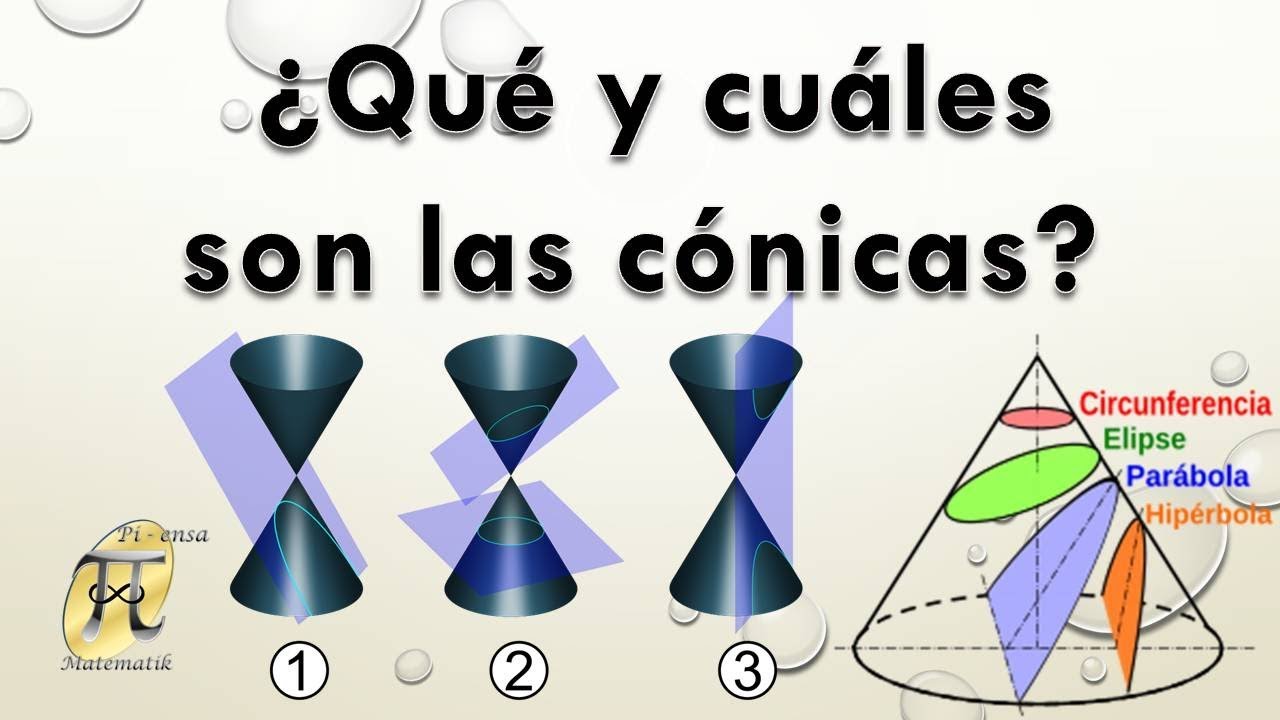
¿Qué son las cónicas?
Las cónicas son un conjunto de curvas geométricas que se obtienen a partir de la intersección de un plano con un cono de doble cono circular. Las cónicas son conocidas desde la antigüedad y han sido estudiadas por matemáticos y geometras durante siglos.
Existen tres tipos de cónicas principales: la elipse, la parábola y la hipérbola.
Elipse
Una elipse es una curva cerrada simétrica con respecto a dos ejes perpendiculares, llamados ejes de simetría. Una elipse tiene dos puntos notables llamados focos, y la suma de las distancias desde cualquier punto de la elipse a los dos focos es constante.
Parábola
Una parábola es una curva simétrica que se obtiene al cortar un cono de forma oblicua. Tiene un punto llamado foco, y la parábola es el lugar geométrico de todos los puntos equidistantes al foco y a la directriz, una recta fija.
Hipérbola
Una hipérbola es una curva abierta que también se obtiene al cortar un cono de forma oblicua. Tiene dos puntos notables llamados focos, y la diferencia de las distancias desde cualquier punto de la hipérbola a los dos focos es constante.
Las cónicas tienen aplicaciones en diversas áreas, como la física, la ingeniería, la arquitectura y la astronomía. Además, las cónicas son de gran importancia en el estudio de las ecuaciones y las propiedades geométricas.
Propiedades de las cónicas
En geometría, las cónicas son una familia de curvas que se obtienen al cortar un cono por un plano. Las cónicas más comunes son la elipse, la hipérbola y la parábola. Cada una de estas curvas posee propiedades únicas y distintivas.
Elipse: La elipse es una curva cerrada en forma de óvalo. Una de las propiedades más importantes de la elipse es que la suma de las distancias de cualquier punto de la curva a dos puntos fijos llamados focos es constante. Además, la elipse tiene dos ejes principales: el eje mayor, que es la línea que pasa por los dos focos, y el eje menor, que es perpendicular al eje mayor y pasa por el centro de la elipse.
Hipérbola: La hipérbola también es una curva abierta con dos ramas. Al igual que la elipse, la hipérbola tiene dos focos, pero en este caso, la diferencia de las distancias de cualquier punto de la curva a los dos focos es constante. La hipérbola también tiene dos ejes principales: el eje transverso, que es la línea que pasa por los dos focos, y el eje conjugado, que es perpendicular al eje transverso y pasa por el centro de la hipérbola.
Parábola: La parábola es una curva abierta y simétrica con una propiedad muy especial: la distancia de cualquier punto de la curva a un punto fijo llamado foco es igual a la distancia de ese punto a una recta llamada directriz. La parábola también tiene un eje principal que es perpendicular a la directriz y pasa por el foco.
Estas propiedades de las cónicas se utilizan en diversos campos, como la astrofísica, la óptica y la arquitectura. Además, las cónicas son la base de muchas ecuaciones matemáticas y son fundamentales en la comprensión de las formas y figuras en el espacio tridimensional.
En resumen, las cónicas son curvas con propiedades geométricas características. La elipse tiene una forma ovalada y la suma de las distancias a los focos es constante. La hipérbola tiene dos ramas y la diferencia de las distancias a los focos es constante. La parábola es una curva simétrica con la propiedad especial de que la distancia al foco es igual a la distancia a la directriz. Estas propiedades son fundamentales para comprender y utilizar las cónicas en diferentes áreas de la ciencia y la geometría.
Ecuaciones de las cónicas
Las cónicas son un tipo de curvas que se forman al intersectar un plano con un cono de doble conicidad. Estas curvas se pueden representar mediante ecuaciones matemáticas que describen su forma y posición.
La ecuación general de las cónicas
Una ecuación general para las cónicas es:
Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0
Donde A, B, C, D, E y F son constantes que determinan las características de la curva. Dependiendo de los valores de estas constantes, se pueden obtener diferentes tipos de cónicas, como elipse, parábola e hipérbola.
La ecuación de una elipse
La ecuación de una elipse centrada en el origen y con semiejes a y b es:
x^2/a^2 + y^2/b^2 = 1
Esta ecuación muestra que la suma de las distancias desde cualquier punto de la elipse hasta los focos es constante.
La ecuación de una parábola
La ecuación de una parábola centrada en el origen y con eje vertical es:
y^2 = 4ax
Donde a es la distancia del vértice de la parábola al foco.
La ecuación de una hipérbola
La ecuación de una hipérbola centrada en el origen y con ejes transverso y conjugado de longitud a y b, respectivamente, es:
x^2/a^2 – y^2/b^2 = 1
Esta ecuación muestra que la diferencia de las distancias desde cualquier punto de la hipérbola hasta los focos es constante.
Aplicaciones de las cónicas
Las cónicas, también conocidas como secciones cónicas, son las curvas resultantes de la intersección de un plano con un cono de doble n- pica. Estas curvas han sido estudiadas y utilizadas durante siglos debido a sus numerosas aplicaciones en diversas áreas.
Aplicaciones en la geometría
- Óptica: Las cónicas se utilizan en la óptica para el diseño de lentes y espejos. Por ejemplo, las lentes convergentes tienen forma de elipse, mientras que las lentes divergentes tienen forma de hipérbola.
- Geodesia: En geodesia, las cónicas se usan para representar la forma de la Tierra en mapas y cartografía. La proyección de Mercator, por ejemplo, utiliza una forma de cilindro para representar las coordenadas geográficas en un plano.
Aplicaciones en la física
- Mecánica celeste: Las cónicas son fundamentales en el estudio de la mecánica celeste. La forma de las órbitas planetarias alrededor del Sol sigue una trayectoria elíptica, lo que fue descubierto por Johannes Kepler.
- Ecuaciones diferenciales: Las cónicas también se utilizan en la resolución de ecuaciones diferenciales en física y matemáticas. Por ejemplo, las ecuaciones de movimiento de un proyectil siguen una trayectoria parabólica.
Aplicaciones en la arquitectura y el diseño
- Arquitectura: Las cónicas se utilizan en la arquitectura para diseñar elementos curvos, como arcos, cúpulas y bóvedas. Por ejemplo, la forma de la cúpula del Panteón de Roma sigue una forma de media esfera.
- Diseño industrial: En diseño industrial, las cónicas se aplican para crear formas ergonómicas y funcionales. Por ejemplo, la forma de un mouse de computadora sigue una forma ovalada que se asemeja a la elipse.
En resumen, las cónicas tienen una amplia gama de aplicaciones en campos como la geometría, la física, la arquitectura y el diseño. Estas curvas nos ayudan a comprender y modelar fenómenos naturales y crear estructuras y productos eficientes y estéticamente agradables.
Ejemplos de problemas resueltos
El objetivo de este artículo es presentar algunos ejemplos de problemas resueltos en diferentes áreas. Estos ejemplos ayudarán a comprender cómo se aplican los conceptos teóricos en situaciones reales.
Problema de matemáticas
Supongamos que tenemos un problema de matemáticas que consiste en encontrar el área de un círculo. Utilizando la fórmula del área del círculo, que es A = πr^2, podemos resolver el problema. Si el radio del círculo es 5 unidades, simplemente sustituimos el valor en la fórmula y obtenemos el área como 78.54 unidades cuadradas.
Problema de física
Imaginemos que tenemos un problema de física que requiere calcular la velocidad de un objeto en caída libre. Utilizando la fórmula de la velocidad en caída libre, que es v = √2gh, podemos determinar la velocidad. Si la altura desde la cual cae el objeto es de 10 metros y la constante de la gravedad es de 9.8 m/s^2, sustituyendo los valores en la fórmula encontramos que la velocidad es de 14 m/s.
Problema de programación
Supongamos que enfrentamos un problema de programación en el cual se nos pide contar la frecuencia de cada letra en un párrafo. Podemos resolver este problema utilizando un bucle y una estructura de datos adecuada. Usando el lenguaje de programación Python, podemos implementar un código que recorra el párrafo y cuente la frecuencia de cada letra. Por ejemplo, si el párrafo es «Hola mundo», el programa nos mostrará que la frecuencia de la letra «o» es 2.
Problema de economía
Imaginemos que tenemos un problema en el campo de la economía que involucra el cálculo del índice de inflación. Para resolver este problema, necesitamos recolectar datos sobre los precios de una canasta de bienes y servicios en diferentes períodos de tiempo. Luego, utilizando la fórmula del índice de inflación, que es (Precio Actual – Precio Anterior) / Precio Anterior, podemos calcular el índice. Por ejemplo, si el precio de la canasta en el período anterior era de $100 y en el período actual es de $120, el índice de inflación sería del 20%.
Problema de biología
Supongamos que nos encontramos con un problema de biología que requiere calcular la concentración de una sustancia en una solución. Para resolver este problema, necesitaríamos conocer la masa de la sustancia y el volumen de la solución. Utilizando la fórmula de la concentración, que es C = masa / volumen, podemos calcular la concentración. Por ejemplo, si la masa de la sustancia es de 10 gramos y el volumen de la solución es de 100 ml, la concentración sería de 0.1 g/ml.
Estos ejemplos ilustran diferentes tipos de problemas resueltos en diversas áreas. La clave para resolver cualquier problema es comprender los conceptos teóricos subyacentes y aplicar las fórmulas o procedimientos adecuados. ¡La práctica constante lleva a mejores habilidades de resolución de problemas!