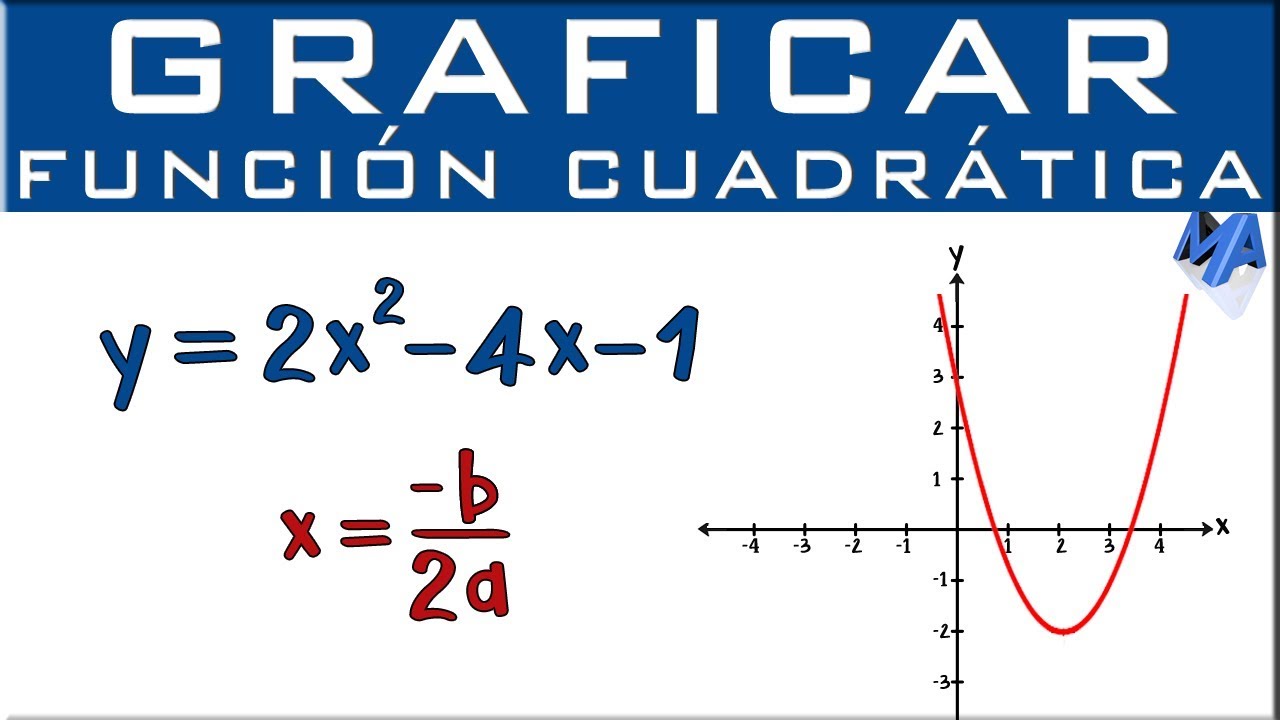
La función cuadrática es un concepto fundamental en el ámbito de las matemáticas. Cuando representa en un gráfico, la curva que forma es de gran importancia para comprender su comportamiento y propiedades. En este artículo, exploraremos en detalle la curva que representa una función cuadrática en un gráfico, así como su significado y aplicaciones. Desde la forma de la curva hasta las intersecciones con los ejes, analizaremos cada aspecto de esta representación visual.
La forma de la curva cuadrática
La curva que representa una función cuadrática en un gráfico tiene una forma distintiva que es ampliamente reconocida. Se caracteriza por ser una parábola, lo que significa que tiene una forma de «U» o de arco. La concavidad de la parábola puede ser hacia arriba o hacia abajo, dependiendo del valor del coeficiente cuadrático en la función cuadrática. Esta forma única es fundamental para comprender el comportamiento de la función y su relación con las raíces, vértices y otros puntos de interés.
Intersecciones con los ejes
Una de las características más destacadas de la curva que representa una función cuadrática en un gráfico es su relación con los ejes coordenados. La parábola corta el eje X en uno, dos o ningún punto, dependiendo de la posición de sus raíces. Estas intersecciones representan los puntos donde la función se anula, es decir, donde su valor es cero. Del mismo modo, la intersección con el eje Y revela el término independiente de la función, proporcionando información crucial sobre su comportamiento asintótico.
Vértice de la parábola
El vértice de la parábola es un punto de particular importancia en la curva que representa una función cuadrática en un gráfico. Este punto corresponde al valor máximo o mínimo de la función, dependiendo de la concavidad de la parábola. El vértice se encuentra en el punto medio entre las raíces de la función, y su coordenada Y revela el valor óptimo de la función. Comprender la ubicación y naturaleza del vértice es esencial para interpretar el comportamiento de la función cuadrática en su totalidad.
Simetría de la parábola
Otro aspecto interesante de la curva que representa una función cuadrática en un gráfico es su simetría. La parábola es simétrica respecto a una línea vertical que pasa por su vértice. Esta simetría es evidente en la forma de la parábola y en la distribución de sus puntos. La comprensión de esta simetría es fundamental para trazar la parábola de manera precisa y para identificar sus propiedades de manera eficiente.
Transformaciones de la parábola
Además de su forma básica, la curva que representa una función cuadrática en un gráfico puede sufrir transformaciones que alteran su posición, orientación y escala. Estas transformaciones incluyen desplazamientos horizontales y verticales, así como estiramientos y compresiones. Comprender cómo estas transformaciones afectan la apariencia de la parábola es esencial para interpretar funciones cuadráticas en diversos contextos matemáticos y aplicados.
Desplazamientos horizontales y verticales
Los desplazamientos horizontales y verticales de una parábola tienen un impacto directo en la ubicación de su vértice y de sus intersecciones con los ejes. Estos desplazamientos pueden ser el resultado de sumar o restar constantes a la función original, lo que desplaza la parábola hacia la izquierda, derecha, arriba o abajo en el plano cartesiano. Entender cómo estos desplazamientos afectan la posición de la parábola es esencial para interpretar sus efectos en el contexto de un problema dado.
Estiramientos y compresiones
Los estiramientos y compresiones modifican la escala de la parábola, afectando su ancho y altura. Estas transformaciones son el resultado de multiplicar constantes a la función original, lo que produce una ampliación o reducción de la parábola en el plano cartesiano. La comprensión de cómo estos cambios afectan la forma de la parábola es fundamental para interpretar sus propiedades geométricas y su relación con otras funciones matemáticas.
Aplicaciones en la vida cotidiana
La curva que representa una función cuadrática en un gráfico tiene numerosas aplicaciones en la vida cotidiana y en diversas disciplinas académicas y profesionales. Desde la física y la ingeniería hasta la economía y la biología, las funciones cuadráticas y sus representaciones gráficas ofrecen herramientas poderosas para modelar fenómenos naturales y sistemas humanos. Comprender la forma y el comportamiento de estas curvas es esencial para aplicar adecuadamente las funciones cuadráticas en situaciones del mundo real.
Modelado de trayectorias y movimientos
En el ámbito de la física y la ingeniería, las funciones cuadráticas y sus gráficos se utilizan comúnmente para modelar la trayectoria de objetos en movimiento, como proyectiles y cuerpos en caída libre. La curva de una función cuadrática representa la forma ideal de estas trayectorias, proporcionando una herramienta poderosa para predecir y analizar el comportamiento de los objetos en el espacio. El estudio detallado de la curva cuadrática en el contexto de estos movimientos es crucial para comprender la física subyacente.
Análisis de costos y beneficios
En el ámbito empresarial y económico, las funciones cuadráticas se utilizan para modelar costos, ingresos, beneficios y otras variables financieras. La representación gráfica de estas funciones proporciona una visión clara de la relación entre diferentes factores económicos, permitiendo a los analistas y tomadores de decisiones comprender mejor el impacto de diversas estrategias y escenarios en el desempeño de una empresa o industria. La capacidad de interpretar y analizar la curva cuadrática es crucial para la toma de decisiones informadas en el ámbito empresarial.
Estudio de fenómenos naturales
En disciplinas como la biología y la ecología, las funciones cuadráticas se utilizan para modelar el crecimiento poblacional, la propagación de enfermedades y otros fenómenos naturales. La representación gráfica de estas funciones permite a los científicos y académicos visualizar y analizar el comportamiento de estos fenómenos a lo largo del tiempo, identificando tendencias, patrones y puntos críticos. La comprensión de la curva que representa una función cuadrática en un gráfico es esencial para interpretar la dinámica de los sistemas naturales.
En resumen, la curva que representa una función cuadrática en un gráfico es un objeto matemático fascinante que ofrece una gran cantidad de información sobre el comportamiento de funciones cuadráticas. Desde su forma básica hasta sus transformaciones y aplicaciones, esta curva desempeña un papel crucial en diversos contextos académicos, profesionales y cotidianos. Comprender en detalle cada aspecto de esta curva es fundamental para dominar el concepto de función cuadrática y su relevancia en el mundo real.