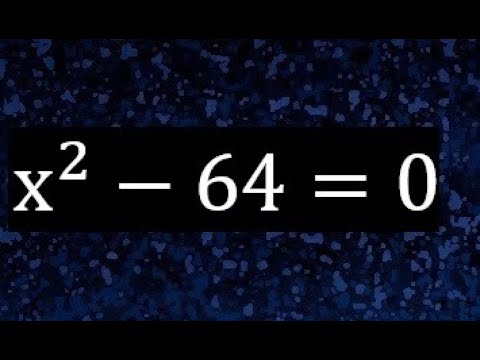La búsqueda de equivalencias matemáticas
La resolución de ecuaciones cuadráticas y la búsqueda de equivalencias entre diferentes ecuaciones es un desafío apasionante para los amantes de las matemáticas. En este artículo, exploraremos la equivalencia de la ecuación (2x)2−64=0 con otra ecuación, utilizando varios métodos y técnicas. Profundizaremos en cada paso, brindando explicaciones detalladas y ejemplos claros para que puedas comprender completamente el proceso.
Expansión de la ecuación
El primer paso para buscar la equivalencia de la ecuación dada es expandirla completamente. La ecuación (2x)2−64=0 puede parecer complicada a simple vista, pero al expandirla paso a paso, podemos simplificarla y trabajar con ella de manera más efectiva. Utilizamos la propiedad distributiva para expandir (2x)2, lo que nos lleva a 4×2. Luego, restamos 64 en ambos lados de la ecuación para obtener la forma estándar de una ecuación cuadrática ax2 + bx + c = 0.
Identificación de coeficientes
Una vez que hemos expandido la ecuación y la hemos llevado a su forma estándar, es crucial identificar los coeficientes a, b y c. En nuestra ecuación (2x)2−64=0, el coeficiente a es 4, el coeficiente b es 0, y el coeficiente c es -64. Estos valores son fundamentales para aplicar la fórmula cuadrática y resolver la ecuación.
Aplicación de la fórmula cuadrática
La fórmula cuadrática es una herramienta poderosa para resolver ecuaciones cuadráticas de la forma ax2 + bx + c = 0. Al sustituir los coeficientes a, b y c en la fórmula cuadrática, podemos encontrar las soluciones de la ecuación. Recordemos que la fórmula cuadrática es x = (-b ± √(b2 – 4ac)) / (2a). Al calcular esta fórmula con los coeficientes de nuestra ecuación, obtendremos las soluciones para x.
Resolución de la ecuación
Después de aplicar la fórmula cuadrática, obtenemos las soluciones para x en la ecuación (2x)2−64=0. Es crucial entender que una ecuación cuadrática puede tener dos soluciones, una solución doble o ninguna solución, dependiendo del discriminante (b2 – 4ac). En este caso específico, calculamos el discriminante y lo utilizamos para determinar las soluciones de la ecuación.
Conexión con una ecuación equivalente
Una vez que hemos resuelto la ecuación inicial, es fascinante explorar su conexión con una ecuación equivalente. La equivalencia entre ecuaciones es un tema central en el ámbito matemático, ya que nos permite ver una misma idea desde diferentes perspectivas y en distintos contextos. Encontrar una ecuación equivalente a (2x)2−64=0 nos lleva a analizar las diferentes formas en que una expresión matemática puede presentarse.
Desglose de la expresión
Para encontrar una ecuación equivalente, descompondremos la expresión (2x)2−64 en sus componentes individuales. Esta fase de desglose nos permitirá identificar patrones, factorizar términos y reorganizar la ecuación de formas creativas. Al descomponer la expresión en pasos lógicos, descubriremos formas alternativas de expresar la misma idea matemática.
Aplicación de identidades algebraicas
La utilización de identidades algebraicas es una herramienta valiosa en la búsqueda de equivalencias entre ecuaciones. Al aplicar identidades algebraicas relevantes, podemos transformar la expresión original en una forma equivalente más manejable. La exploración de identidades como a2 – b2 = (a + b)(a – b) nos brinda insigths sobre cómo reorganizar la ecuación de maneras creativas.
Substitución inteligente
La técnica de substitución inteligente nos permite reescribir la expresión original de maneras innovadoras. Al sustituir ciertos términos por variables o expresiones equivalentes, podemos simplificar la ecuación o llevarla a una forma más reconocible. La elección de las substituciones se basa en la intuición matemática y en la búsqueda de patrones significativos en la expresión.
Transformación en una ecuación cuadrática familiar
Al utilizar las técnicas previas, como el desglose de la expresión, la aplicación de identidades algebraicas y la substitución inteligente, podemos transformar la ecuación (2x)2−64=0 en una ecuación cuadrática más reconocible. Esta transformación nos brinda una nueva perspectiva sobre la ecuación, facilitando su manipulación y análisis desde diferentes ángulos matemáticos.
Exploración de soluciones alternativas
Ahora que hemos encontrado una ecuación equivalente y la hemos transformado en una forma más reconocible, es el momento de explorar soluciones alternativas. La solución de una ecuación puede presentarse de diversas maneras, y al explorar diferentes enfoques, podemos descubrir soluciones más elegantes, simples o generales. Este proceso de exploración creativa amplía nuestra comprensión de la ecuación y sus posibles soluciones.
Relación con otras ramas de las matemáticas
La búsqueda de equivalencias matemáticas no solo se limita al ámbito de las ecuaciones cuadráticas. Existe una conexión profunda entre la equivalencia de ecuaciones y otros conceptos matemáticos, como las identidades trigonométricas, las transformaciones geométricas y la teoría de números. Explorar esta relación nos permite comprender mejor cómo las ideas matemáticas están interconectadas y se entrelazan en un vasto entramado de conceptos.
Generalización y abstracción
Al encontrar la equivalencia de la ecuación (2x)2−64=0 con otra ecuación, estamos practicando la habilidad fundamental de generalización y abstracción en matemáticas. La generalización nos permite ver más allá de una sola ecuación y comprender sus patrones y propiedades en un contexto más amplio. La abstracción nos brinda las herramientas para representar conceptos matemáticos de manera abstracta y simbólica.
Aplicaciones prácticas
Aunque la búsqueda de equivalencias matemáticas puede parecer un ejercicio puramente teórico, su importancia se refleja en numerosas aplicaciones prácticas. Las equivalencias matemáticas se utilizan en la resolución de problemas de ingeniería, la optimización de algoritmos, la criptografía y muchas otras áreas. Al comprender y dominar el arte de encontrar equivalencias, estamos fortaleciendo nuestras habilidades para abordar desafíos del mundo real.
En conclusión, la búsqueda de equivalencias matemáticas es un proceso cautivador que nos invita a explorar la profundidad y la belleza de las ecuaciones. Desde la expansión de la ecuación inicial hasta la exploración de soluciones alternativas, cada paso nos brinda la oportunidad de desarrollar nuestras habilidades matemáticas y comprender la conexión entre diferentes expresiones matemáticas. Al dominar este proceso, no solo fortalecemos nuestra comprensión de las ecuaciones, sino que también ampliamos nuestra visión de las interrelaciones dentro de las matemáticas y su aplicación en el mundo real.