La hipotenusa de un triángulo rectángulo mide 15 cm

¿Qué es un triángulo rectángulo?

Un triángulo rectángulo es un tipo de triángulo que posee un ángulo recto, es decir, un ángulo de 90 grados. Este ángulo se encuentra en la intersección de dos de sus lados, lo que le otorga una forma particularmente característica.

Un triángulo rectángulo está compuesto por tres lados: el cateto opuesto, el cateto adyacente y la hipotenusa. El cateto opuesto es el lado que se opone al ángulo recto, mientras que el cateto adyacente es el lado que forma el ángulo recto junto con otro lado. Por último, la hipotenusa es el lado opuesto al ángulo recto y es el lado más largo del triángulo.

Una propiedad importante del triángulo rectángulo es que el teorema de Pitágoras se aplica a él. Este teorema establece que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Es decir, si a y b son los catetos y c es la hipotenusa, entonces se cumple que a^2 + b^2 = c^2.

En geometría, los triángulos rectángulos son utilizados en diferentes aplicaciones, como la resolución de problemas de trigonometría o el cálculo de medidas en ingeniería y arquitectura. Además, son fundamentales en la construcción de figuras y en la resolución de problemas prácticos.

En resumen, un triángulo rectángulo es un tipo de triángulo que posee un ángulo recto de 90 grados. Se compone de un cateto opuesto, un cateto adyacente y una hipotenusa, y se rige por el teorema de Pitágoras. Su utilidad en la geometría y otras disciplinas es indiscutible.

Propiedad del teorema de Pitágoras

El teorema de Pitágoras es una propiedad fundamental en geometría que establece la relación entre los lados de un triángulo rectángulo.

La fórmula del teorema de Pitágoras es: c² = a² + b², donde “c” representa la hipotenusa del triángulo y “a” y “b” representan los catetos.

Este teorema es especialmente útil para calcular la longitud de un lado desconocido de un triángulo rectángulo si se conocen los otros dos lados.

Por ejemplo, si tenemos un triángulo rectángulo con un cateto de longitud 3 unidades y otro cateto de longitud 4 unidades, podemos usar el teorema de Pitágoras para encontrar la longitud de la hipotenusa:

3² + 4² = c²

Simplificando la ecuación: 9 + 16 = c²

25 = c²

Finalmente, podemos resolver la ecuación tomando la raíz cuadrada de ambos lados:

c = √25

c = 5

Por lo tanto, la longitud de la hipotenusa es 5 unidades.

Aplicaciones prácticas del teorema de Pitágoras

• La geometría: el teorema de Pitágoras es ampliamente utilizado en geometría para resolver problemas relacionados con triángulos rectángulos.
• La arquitectura: los arquitectos utilizan el teorema de Pitágoras para asegurarse de que las estructuras sean estables y estén correctamente alineadas.
• La física: en física, el teorema de Pitágoras se aplica en cálculos relacionados con la velocidad y la aceleración de un objeto en movimiento.

Puedes encontrar ejemplos de aplicaciones del teorema de Pitágoras en muchos campos diferentes, ya que es una herramienta fundamental en matemáticas y ciencias.

Aplicando el teorema de Pitágoras

El teorema de Pitágoras es uno de los conceptos fundamentales en geometría.

Enunciado del teorema: En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Este teorema permite calcular la longitud de un lado desconocido de un triángulo rectángulo si conocemos los valores de los otros dos lados.

Fórmula del teorema de Pitágoras:

c^2 = a^2 + b^2

En donde c es la hipotenusa y a y b son los catetos del triángulo rectángulo.

Para aplicar el teorema de Pitágoras, primero debemos identificar cuál es la hipotenusa y cuáles son los catetos.

Ejemplo:

Supongamos que tenemos un triángulo rectángulo con dos catetos de longitudes conocidas, a = 3 y b = 4.

Para encontrar la longitud de la hipotenusa, podemos utilizar la fórmula del teorema de Pitágoras. Reemplazamos los valores de a y b en la fórmula:

c^2 = 3^2 + 4^2

c^2 = 9 + 16

c^2 = 25

Finalmente, calculamos la raíz cuadrada de 25 para obtener el valor de c:

c = sqrt(25)

c = 5

Por lo tanto, la longitud de la hipotenusa es igual a 5.

El teorema de Pitágoras es una herramienta fundamental en matemáticas y tiene múltiples aplicaciones en la resolución de problemas geométricos y trigonométricos.

Cálculo de los catetos

El cálculo de los catetos de un triángulo rectángulo es una tarea común en geometría. Los catetos son los dos lados que forman el ángulo recto en un triángulo rectángulo, y encontrar su longitud puede ser útil para resolver problemas de geometría o trigonometría.

Existen diferentes formas de calcular los catetos de un triángulo rectángulo, dependiendo de la información que se tenga sobre el triángulo. A continuación, vamos a repasar algunos de los métodos más utilizados:

Método de Pitágoras:

El teorema de Pitágoras establece que en un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Esto nos da la fórmula:

a^2 + b^2 = c^2

Donde “c” es la hipotenusa y “a” y “b” son los catetos.

Si conocemos la longitud de la hipotenusa y uno de los catetos, podemos despejar el otro cateto utilizando la fórmula:

b = sqrt(c^2 – a^2)

O si conocemos la longitud de un cateto y la hipotenusa, podemos despejar el otro cateto utilizando la fórmula:

a = sqrt(c^2 – b^2)

Razones trigonométricas:

Otro método para calcular los catetos de un triángulo rectángulo es utilizando razones trigonométricas. Las razones trigonométricas son funciones matemáticas que relacionan los ángulos de un triángulo con las longitudes de sus lados.

Si conocemos uno de los ángulos agudos del triángulo y la longitud de uno de los catetos, podemos utilizar la función trigonométrica correspondiente para calcular el otro cateto.

Por ejemplo, si conocemos el ángulo agudo “α” y la longitud del cateto “a”, podemos utilizar la función seno para calcular el cateto “b”. La fórmula sería:

b = a * sin(α)

De manera similar, si conocemos el ángulo agudo “β” y la longitud del cateto “b”, podemos utilizar la función coseno para calcular el cateto “a”. La fórmula sería:

a = b * cos(β)

Aplicación práctica:

El cálculo de los catetos puede ser útil en diversas situaciones. Por ejemplo, si conocemos la altura de un edificio y la distancia desde la base hasta un punto de observación, podemos utilizar el cálculo de los catetos para determinar la distancia horizontal entre el punto de observación y el edificio.

Además, el cálculo de los catetos es fundamental para resolver problemas de trigonometría, como el cálculo de ángulos desconocidos o la determinación de la longitud de lados en triángulos rectángulos.

En conclusión, el cálculo de los catetos de un triángulo rectángulo es una habilidad matemática importante que puede ser utilizada en varios contextos. Ya sea utilizando el teorema de Pitágoras o las razones trigonométricas, conocer cómo calcular los catetos nos permite resolver problemas y obtener información relevante sobre triángulos rectángulos.

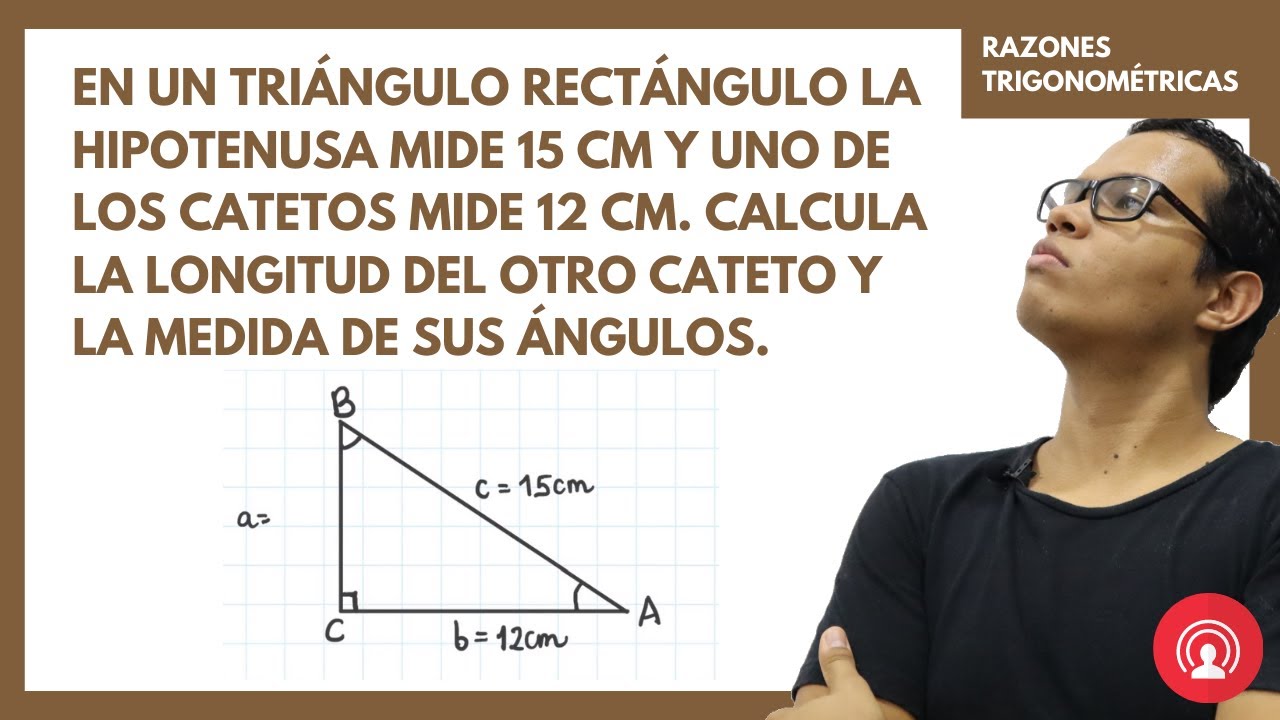
Resultado de los catetos

El resultado de los catetos se refiere a la solución de un problema relacionado con un triángulo rectángulo. En este tipo de triángulo, uno de los ángulos es de 90 grados y los otros dos son agudos.

Los catetos son los dos lados más cortos del triángulo rectángulo, que forman el ángulo recto. Su longitud puede ser conocida o desconocida.

Para encontrar el resultado de los catetos, se pueden utilizar diferentes fórmulas en función de la información disponible. Si conocemos la hipotenusa y un cateto, podemos usar el teorema de Pitágoras para encontrar el valor del cateto restante. La fórmula es la siguiente:

c² = a² + b²

Donde c representa la hipotenusa y a y b son los catetos. Aquí, usamos la etiqueta HTML strong para resaltar la fórmula.

Si conocemos los ángulos del triángulo rectángulo, podemos utilizar las razones trigonométricas para encontrar el valor de los catetos. Por ejemplo, si conocemos el ángulo agudo y la hipotenusa, podemos utilizar la función seno para encontrar el cateto opuesto. La fórmula correspondiente es:

a = c * sen(θ)

Donde a representa el cateto opuesto, c es la hipotenusa y θ es el ángulo agudo. Aquí, utilizamos la etiqueta HTML strong para destacar la fórmula.

En resumen, el resultado de los catetos se refiere a la solución de un triángulo rectángulo, ya sea mediante el uso del teorema de Pitágoras o de las razones trigonométricas. A través de estas fórmulas, podemos encontrar los valores de los catetos en función de la información disponible.