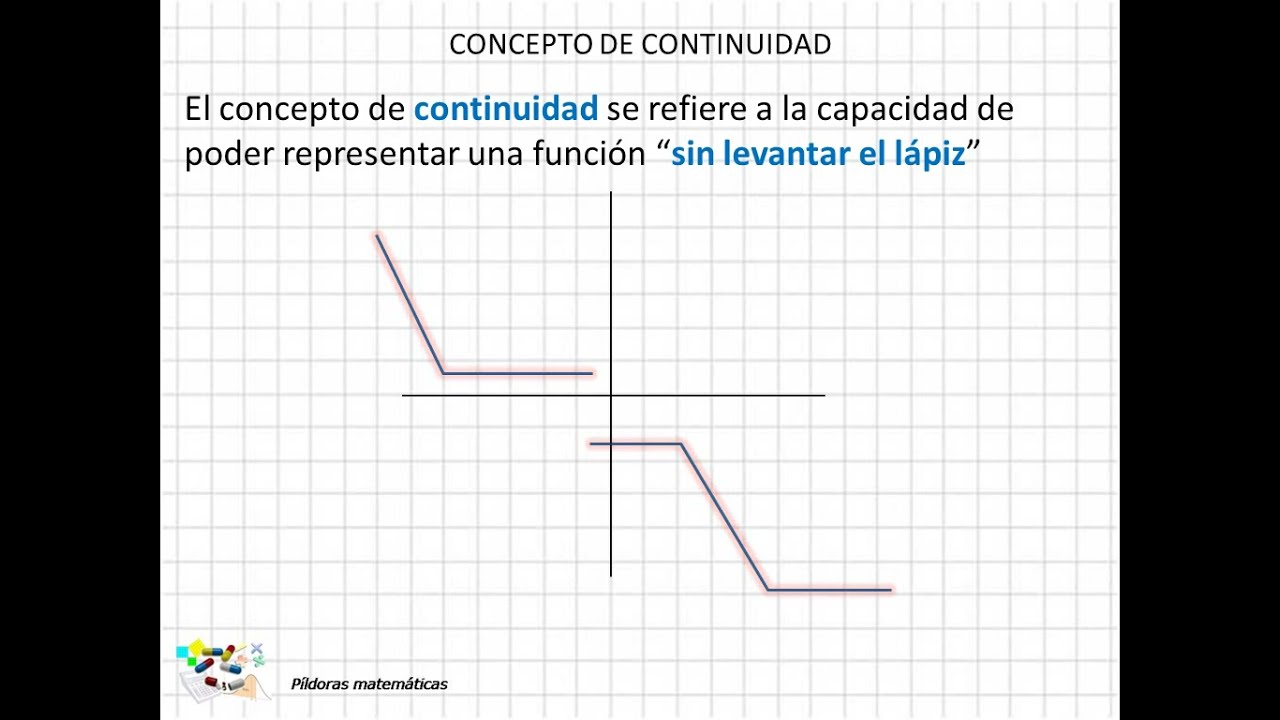
¿Qué es la continuidad en una función?
La continuidad en una función es un concepto fundamental en matemáticas que describe la suavidad y cohesión de una función en un intervalo específico. Una función se considera continua si no hay interrupciones, saltos o discontinuidades en su gráfico. La continuidad de una función es crucial en diversos campos, incluyendo el cálculo, la física y la ingeniería, donde se utiliza para modelar fenómenos naturales y analizar el comportamiento de sistemas.
Tipos de discontinuidades
Existen varios tipos de discontinuidades que pueden presentarse en una función, como las discontinuidades removibles, las discontinuidades de salto y las discontinuidades infinitas. Cada tipo de discontinuidad afecta la continuidad de la función en diferentes formas, lo que subraya la importancia de comprender y analizar la continuidad en el estudio de funciones.
El papel de la continuidad en el análisis matemático
En el análisis matemático, la continuidad es fundamental para comprender el comportamiento de funciones y desarrollar técnicas para la resolución de problemas. La continuidad de una función en un intervalo determinado garantiza que no haya cambios bruscos o anomalías en su comportamiento, lo que facilita la interpretación de su gráfico y la predicción de su evolución.
La continuidad como requisito para la diferenciabilidad
En el cálculo diferencial, la continuidad es un requisito previo para la diferenciabilidad de una función en un punto específico. La existencia de la derivada de una función en un punto depende directamente de su continuidad en dicho punto. Por lo tanto, la continuidad es un aspecto crucial en la determinación de la existencia de la pendiente de una función en un punto dado.
El teorema del valor intermedio
Una consecuencia directa de la continuidad de una función es el teorema del valor intermedio, el cual establece que si una función es continua en un intervalo cerrado, entonces toma todos los valores intermedios comprendidos entre el valor de la función en los extremos del intervalo. Este resultado es fundamental en el análisis de funciones continuas y proporciona información relevante sobre sus comportamientos globales.
La importancia práctica de la continuidad en la física y la ingeniería
En la física y la ingeniería, la continuidad de funciones es esencial para modelar fenómenos naturales y diseñar sistemas que operen de manera suave y predecible. Las leyes físicas y los principios de la ingeniería se basan en el supuesto de que las funciones que describen el comportamiento de sistemas son continuas, lo que subraya la relevancia de este concepto en la práctica.
Aplicaciones en la modelización de sistemas dinámicos
En la modelización de sistemas dinámicos, la continuidad de las funciones que describen variables como la velocidad, la posición y la aceleración es esencial para predecir y controlar el comportamiento de estos sistemas. La continuidad garantiza que no haya cambios abruptos en las variables, lo que facilita el diseño de estrategias de control y optimización.
Indicadores de estabilidad en sistemas físicos
La continuidad de las funciones que representan los fenómenos físicos es un indicador crucial de la estabilidad de los sistemas. Las funciones continuas permiten analizar y predecir la evolución de sistemas físicos sin discontinuidades o comportamientos inesperados, lo que es fundamental para garantizar la seguridad y eficacia de estos sistemas en la práctica.
La continuidad y la evolución de fenómenos naturales
En el estudio de fenómenos naturales, la continuidad en las funciones que describen variables como la temperatura, la presión y la densidad es esencial para comprender la evolución y la interacción de estos fenómenos en el tiempo y el espacio. La continuidad permite analizar cambios graduales y predecir tendencias a largo plazo en diferentes contextos naturales.
Aplicaciones en la meteorología y la climatología
En la meteorología y la climatología, la continuidad de las funciones que modelan variables atmosféricas como la temperatura y la humedad es crucial para comprender y predecir fenómenos climáticos. La continuidad de estas funciones permite realizar pronósticos a largo plazo y analizar tendencias climáticas con mayor precisión.
Interacciones ecológicas y continuidad de funciones
En el estudio de las interacciones ecológicas, la continuidad en las funciones que representan poblaciones, tasas de crecimiento y flujos de energía es fundamental para comprender la dinámica de los ecosistemas y predecir el impacto de cambios ambientales. La continuidad de estas funciones facilita el análisis de relaciones ecológicas a largo plazo y ayuda a diseñar estrategias de conservación y manejo sostenible de recursos naturales.
El desafío de garantizar la continuidad en sistemas y modelos matemáticos
Aunque la continuidad es un concepto fundamental en matemáticas y ciencias aplicadas, garantizar su presencia en sistemas y modelos matemáticos puede resultar un desafío en ciertos contextos. Fenómenos como transiciones de fase, cambios abruptos y discontinuidades físicas presentan dificultades para mantener la continuidad en las funciones que los describen, lo que demanda la aplicación de enfoques y técnicas específicas para abordar estos desafíos.
Desarrollo de modelos no continuos
En algunos casos, el desarrollo de modelos matemáticos no continuos es necesario para representar fenómenos que presentan discontinuidades o cambios bruscos. La teoría de distribuciones y el cálculo de variaciones son herramientas matemáticas que permiten trabajar con funciones no continuas y abordar problemas donde la continuidad presenta dificultades.
Papel de la teoría del caos en sistemas no lineales
En sistemas dinámicos no lineales, la teoría del caos revela fenómenos de sensibilidad a las condiciones iniciales y comportamientos no lineales que desafían la continuidad de las funciones que describen dichos sistemas. El estudio de sistemas caóticos requiere enfoques matemáticos especializados para comprender la evolución de estos sistemas en el tiempo y el espacio.
La continuidad como base para el análisis y la predicción
En resumen, la continuidad en una función es un concepto esencial en matemáticas y disciplinas aplicadas que permite comprender, analizar y predecir el comportamiento de sistemas y fenómenos naturales. La importancia de la continuidad se extiende desde el cálculo y el análisis matemático hasta la modelización de sistemas físicos y la comprensión de interacciones naturales, destacando su papel en el desarrollo de teorías y aplicaciones en diversos campos del conocimiento.
Consideraciones para el desarrollo de sistemas y modelos matemáticos
Al enfrentar el desafío de garantizar la continuidad en sistemas y modelos matemáticos, es crucial considerar las limitaciones y posibilidades de los enfoques matemáticos disponibles, así como la naturaleza de los fenómenos que se pretende modelar. La aplicación de técnicas avanzadas y la exploración de enfoques no convencionales son aspectos fundamentales para abordar la complejidad de la continuidad en contextos específicos.