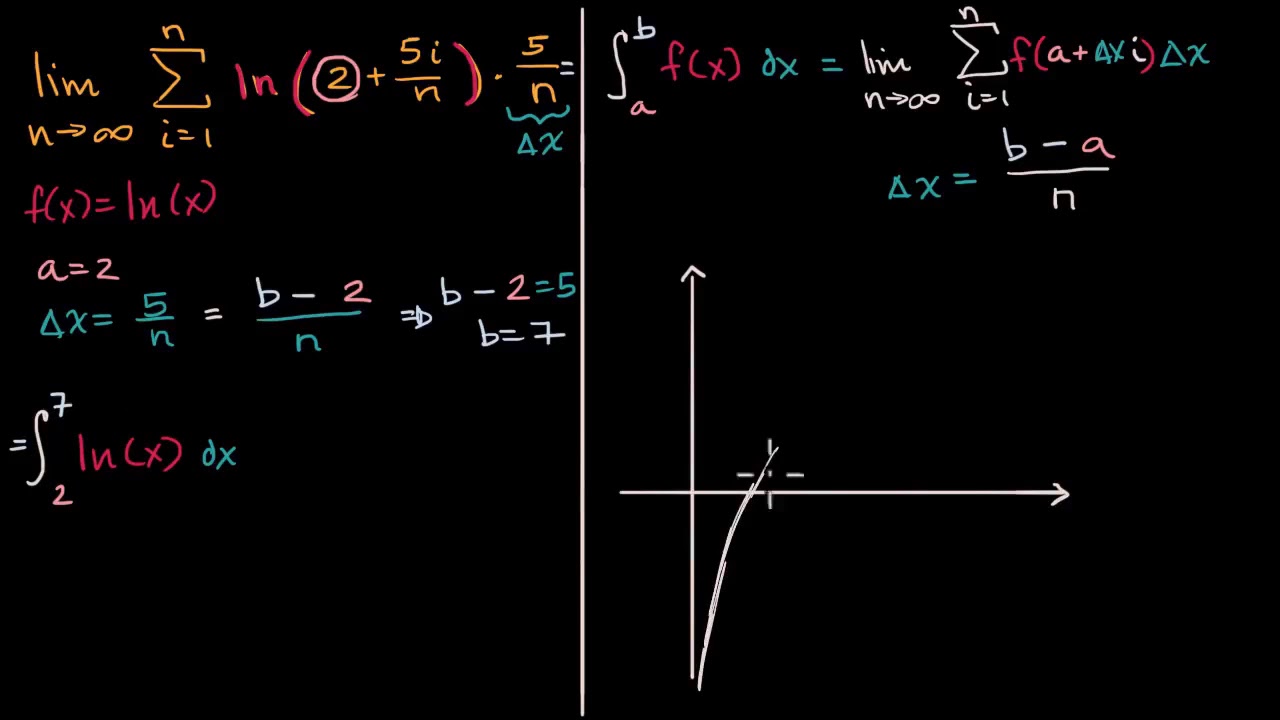La integral definida es un concepto fundamental en el cálculo que nos permite encontrar el área debajo de una curva. Al entenderla como el límite de una suma de áreas, podemos apreciar su importancia y su aplicación en diferentes campos de la ciencia y la ingeniería.
El concepto de integral definida
Antes de sumergirnos en el límite de una suma de áreas, es importante comprender qué es exactamente una integral definida. En pocas palabras, la integral definida de una función en un intervalo dado representa el área bajo la curva de esa función en ese intervalo. Este concepto es esencial para resolver problemas de cálculo, como encontrar áreas, volúmenes, y calcular el trabajo realizado por una fuerza variable.
El límite de una suma de áreas
Al observar la integral definida desde la perspectiva del límite de una suma de áreas, podemos apreciar cómo se relaciona con el cálculo y entender su utilidad en la resolución de problemas. Este enfoque nos permite visualizar la integral como la acumulación de infinitas áreas de rectángulos bajo una curva, cada vez más precisos a medida que el número de rectángulos aumenta.
El proceso de aproximación
Para comprender mejor el límite de una suma de áreas, es útil imaginar dividir el área bajo la curva en múltiples rectángulos. A medida que el número de rectángulos aumenta, su ancho disminuye, y la altura se ajusta para que coincida con la función en un punto específico. Este proceso de aproximación nos ayuda a visualizar cómo la suma de estas áreas de rectángulos se aproxima al área real bajo la curva a medida que el número de rectángulos aumenta infinitamente.
La importancia de la precisión
Al considerar el límite de una suma de áreas, es crucial reconocer la importancia de la precisión en el cálculo de la integral definida. Cuanto más refinada sea la partición del intervalo y más pequeños sean los rectángulos, mayor será la precisión con la que la suma de áreas de rectángulos se aproxima al área real bajo la curva. Esta precisión es fundamental en aplicaciones que requieren resultados exactos, como en la física y la ingeniería.
La conexión con el infinito
El límite de una suma de áreas nos lleva a enfrentar la noción de infinito en el contexto del cálculo. A medida que el número de rectángulos en la partición del intervalo tiende a infinito, la aproximación de la suma de áreas se acerca cada vez más al valor real del área bajo la curva. Esta conexión con el infinito es fundamental para comprender la naturaleza de la integral definida y su capacidad para representar cantidades continuas y acumulativas.
La representación gráfica
Visualizar la integral definida como el límite de una suma de áreas nos lleva a considerar su representación gráfica. Al observar un gráfico de una función y su área bajo la curva en un intervalo dado, podemos apreciar cómo se relaciona con la idea de acumulación de áreas de rectángulos. Esta representación gráfica nos brinda una comprensión intuitiva de cómo la integral definida se aproxima al área real bajo la curva a medida que refinamos la partición del intervalo.
La aplicabilidad en problemas del mundo real
Comprender la integral definida como el límite de una suma de áreas nos permite aplicar este concepto en la resolución de problemas del mundo real. Desde calcular el área bajo una curva hasta determinar el volumen de sólidos de revolución, la integral definida desempeña un papel crucial en campos como la física, la ingeniería y la economía. Al ver la integral como la acumulación de áreas, podemos abordar problemas de manera más efectiva y comprender mejor su relevancia en el mundo que nos rodea.
La importancia de la integral definida
Reconocer la integral definida como el límite de una suma de áreas resalta su importancia en el marco del cálculo y su aplicabilidad en diversas disciplinas. Esta comprensión nos permite utilizar la integral definida como una herramienta poderosa para resolver problemas y modelar fenómenos del mundo real, lo que subraya su valor en el ámbito académico y profesional.
La utilidad en el cálculo de áreas
Una de las aplicaciones más inmediatas de la integral definida es el cálculo de áreas. Al interpretarla como la acumulación de áreas de rectángulos, podemos determinar con precisión el área bajo una curva, incluso cuando esta curva no sigue una forma geométrica simple. Esta capacidad de calcular áreas de regiones irregulares es fundamental en la resolución de problemas de geometría y en la determinación de superficies y volúmenes en el espacio tridimensional.
La medición de volúmenes
Al extender la idea de la integral definida como el límite de una suma de áreas, podemos aplicarla al cálculo de volúmenes de sólidos. Al rotar una región acotada alrededor de un eje, la integral definida nos permite encontrar el volumen del sólido resultante. Este enfoque nos brinda una herramienta fundamental en la resolución de problemas de volumetría y nos permite abordar situaciones tridimensionales de manera precisa y rigurosa.
La modelización de fenómenos físicos
En el campo de la física, la integral definida desempeña un papel crucial en la modelización de fenómenos físicos y la determinación de cantidades acumulativas. Al entenderla como la acumulación de áreas de rectángulos, podemos aplicarla para representar la energía acumulada, el trabajo realizado por una fuerza variable, o la masa total de un objeto con densidad variable. Este enfoque nos permite comprender mejor la relación entre la integral definida y la física, y su capacidad para representar cantidades continuas en el tiempo.
La ingeniería y la integral definida
En el ámbito de la ingeniería, la integral definida como el límite de una suma de áreas es esencial para resolver problemas de diseño, análisis estructural, y optimización de recursos. Al utilizarla para calcular momentos de inercia, centros de masa, o flujos de fluidos, los ingenieros pueden modelar fenómenos físicos con precisión y tomar decisiones fundamentadas en el diseño y la implementación de sistemas complejos. Esta aplicación de la integral definida destaca su importancia en ingeniería y su influencia en el desarrollo de tecnologías y procesos innovadores.
La conexión con la economía
En el ámbito económico, la integral definida como el límite de una suma de áreas es fundamental para el cálculo de cantidades acumulativas, como el ingreso total, la producción acumulada, o la acumulación de recursos en el tiempo. Al comprender este concepto, los economistas y analistas financieros pueden modelar de manera precisa el comportamiento de variables económicas a lo largo del tiempo, lo que les brinda herramientas poderosas para la toma de decisiones y la formulación de políticas económicas.
La integral definida en el contexto académico
A nivel académico, la integral definida desempeña un papel crucial en la formación en matemáticas, física, ingeniería, economía, y otras disciplinas. Comprenderla como el límite de una suma de áreas no solo amplía la comprensión de los estudiantes sobre el cálculo, sino que también les brinda una herramienta poderosa para abordar problemas complejos y modelar fenómenos del mundo real. Esta integración de la integral definida en el currículo académico subraya su importancia en la educación y su papel en el desarrollo de habilidades analíticas y de modelado.
En conclusión, la integral definida como el límite de una suma de áreas es un concepto fundamental que trasciende las fronteras del cálculo y se integra en diferentes campos de la ciencia y la ingeniería. Al comprender su importancia, su aplicabilidad, y su conexión con el infinito, podemos apreciar su valor como una herramienta poderosa para resolver problemas del mundo real y modelar fenómenos continuos. Esta comprensión nos brinda una visión más profunda de cómo la integral definida enriquece nuestra comprensión del mundo que nos rodea y nos proporciona herramientas fundamentales para abordar desafíos complejos en diversos ámbitos.