Qué es un triángulo rectángulo
Un triángulo rectángulo es un tipo especial de triángulo que tiene uno de sus ángulos internos igual a 90 grados. Además, en este tipo de triángulo, los lados que forman el ángulo recto son llamados catetos, mientras que el lado opuesto al ángulo recto se conoce como hipotenusa.
La propiedad más importante de un triángulo rectángulo es el famoso teorema de Pitágoras, el cual establece que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Esta relación matemática es muy útil para resolver problemas relacionados con medidas de triángulos rectángulos.
Además, los triángulos rectángulos son frecuentemente utilizados en trigonometría, dado que las razones trigonométricas (seno, coseno y tangente) están definidas en función de los ángulos de un triángulo rectángulo.
En resumen, un triángulo rectángulo es un tipo de triángulo con un ángulo interno igual a 90 grados, donde uno de los lados es la hipotenusa y los otros dos lados son los catetos. El teorema de Pitágoras, así como las razones trigonométricas, son conceptos esenciales asociados a este tipo de triángulo.
Qué son el cateto opuesto y el cateto adyacente
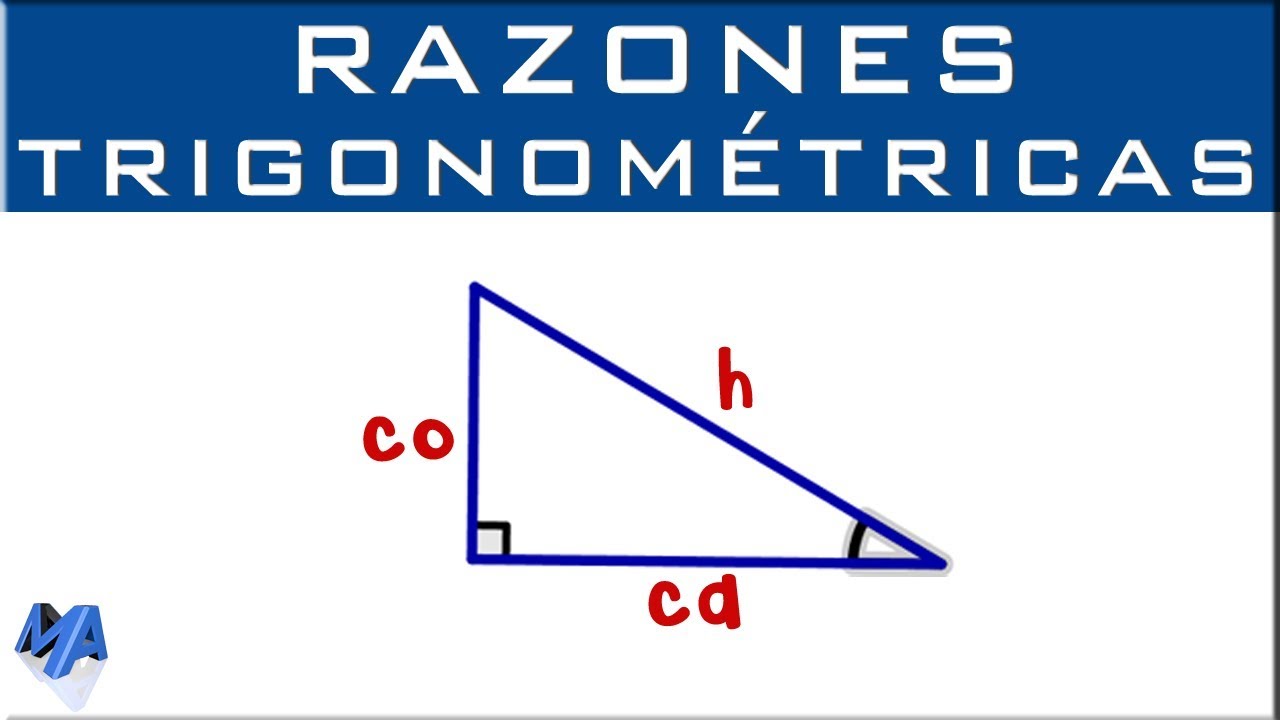
Un triángulo rectángulo tiene un ángulo de 90 grados y dos lados perpendiculares llamados catetos. El cateto opuesto es el lado que se opone al ángulo de interés, mientras que el cateto adyacente es el lado que está próximo a ese ángulo.
El cateto opuesto se encuentra en la misma línea que el ángulo y se extiende hacia arriba o hacia abajo desde el vértice del ángulo recto. Por otro lado, el cateto adyacente se encuentra junto al ángulo recto, formando uno de los dos lados que lo componen.
En resumen, el cateto opuesto es el lado que se opone al ángulo de interés, mientras que el cateto adyacente es el lado que está próximo a ese ángulo. Ambos catetos son elementos fundamentales en la geometría y trigonometría cuando se trabaja con triángulos rectángulos.
Relación entre el cateto opuesto y el cateto adyacente
El cateto opuesto y el cateto adyacente son dos de los lados de un triángulo rectángulo. La relación entre ellos está dada por la función trigonométrica llamada tangente.
Definiciones:
- Cateto opuesto: El cateto opuesto es el lado que se encuentra en frente del ángulo recto en un triángulo rectángulo.
- Cateto adyacente: El cateto adyacente es el lado que forma un ángulo junto al ángulo recto en un triángulo rectángulo.
La relación entre el cateto opuesto y el cateto adyacente se expresa mediante la función trigonométrica tangente, que se denota como tan(theta). La tangente de un ángulo es igual al cociente del cateto opuesto dividido por el cateto adyacente.
Matemáticamente, la fórmula para la tangente es la siguiente:
tan(theta) = cateto opuesto / cateto adyacente
Esta relación es de gran importancia en trigonometría, ya que permite calcular el valor de un ángulo desconocido cuando se conocen las longitudes de los catetos opuesto y adyacente.
Es necesario resaltar que la tangente solo es válida en un triángulo rectángulo, donde uno de los ángulos es de 90 grados. Además, la función tangente tiene propiedades y características diferentes a las otras funciones trigonométricas, como el seno y el coseno.
Conclusión:
En resumen, la relación entre el cateto opuesto y el cateto adyacente se expresa mediante la función trigonométrica tangente. Esta relación es fundamental para calcular ángulos desconocidos en un triángulo rectángulo y tiene diversas aplicaciones en campos como la ingeniería, la física y la geometría.
Fórmula de la tangente
La fórmula de la tangente es una de las más importantes en la trigonometría. Permite calcular la relación entre los lados de un triángulo rectángulo y sus ángulos.
La fórmula de la tangente se expresa de la siguiente manera:
tan(θ) = sen(θ) / cos(θ)
Donde “θ” representa el ángulo en cuestión.
Esta fórmula nos muestra que la tangente de un ángulo es igual al cociente entre el seno y el coseno de ese ángulo.
Es importante tener en cuenta que la fórmula de la tangente solo es válida para triángulos rectángulos. Además, la tangente puede tomar valores positivos, negativos o infinitos, dependiendo del ángulo en cuestión.
Otra forma de representar la fórmula de la tangente es utilizando las funciones trigonométricas en su definición original:
- tan(θ) = sin(θ) / cos(θ)
- tan(θ) = y / x
Donde “sin(θ)” representa el seno del ángulo, “cos(θ)” representa el coseno del ángulo, y “x” e “y” son las longitudes de los catetos del triángulo rectángulo.
La fórmula de la tangente es muy útil en diversas aplicaciones, como la resolución de problemas relacionados con la altura de un objeto, la pendiente de una recta o el cálculo de distancias. Además, es fundamental en el estudio de la trigonometría y la geometría.
En resumen, la fórmula de la tangente nos permite calcular la relación entre los lados de un triángulo rectángulo y sus ángulos. Es una de las fórmulas más importantes dentro de la trigonometría y tiene múltiples aplicaciones en diversas áreas. Recuerda utilizar las funciones trigonométricas para aplicar esta fórmula correctamente.
Ejemplo de cálculo de la relación
Para comprender cómo se calcula la relación entre dos variables, tomemos como ejemplo el aumento salarial de los empleados en una empresa en función de su antigüedad.
Supongamos que tenemos los siguientes datos:
- Empleado A: 1 año de antigüedad, salario actual de $1000
- Empleado B: 3 años de antigüedad, salario actual de $1500
- Empleado C: 5 años de antigüedad, salario actual de $2000
El primer paso para calcular la relación sería determinar el incremento salarial de cada empleado. Esto se puede hacer restando el salario actual del salario inicial:
Para el Empleado A:
Incremento = Salario actual – Salario inicial
Incremento = $1000 – $0 = $1000
Para el Empleado B:
Incremento = Salario actual – Salario inicial
Incremento = $1500 – $0 = $1500
Para el Empleado C:
Incremento = Salario actual – Salario inicial
Incremento = $2000 – $0 = $2000
Una vez que tenemos los incrementos salariales, podemos calcular la relación dividiendo el incremento entre la antigüedad de cada empleado:
Para el Empleado A:
Relación = Incremento / Antigüedad
Relación = $1000 / 1 año = $1000
Para el Empleado B:
Relación = Incremento / Antigüedad
Relación = $1500 / 3 años = $500
Para el Empleado C:
Relación = Incremento / Antigüedad
Relación = $2000 / 5 años = $400
Al calcular la relación, podemos observar que el Empleado A tiene la mayor relación ya que ha experimentado un incremento de $1000 por cada año de antigüedad.
En resumen, el cálculo de la relación se realiza determinando el incremento salarial de cada empleado y dividiendo ese incremento entre su antigüedad. Esto nos permite comparar la relación entre diferentes variables y entender cómo están relacionadas entre sí.