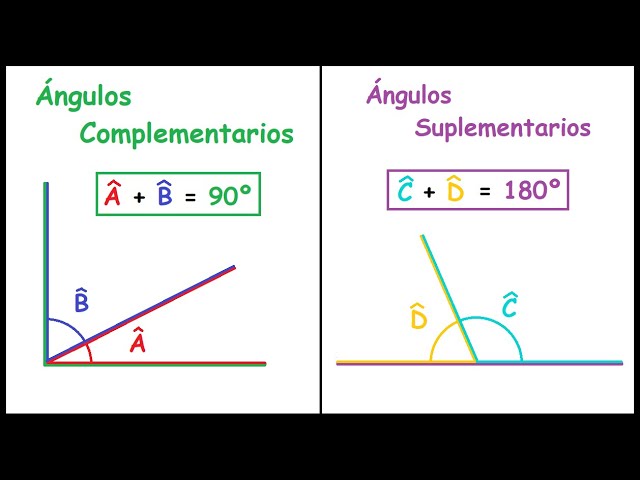
¿Qué es un ángulo suplementario?
Un ángulo suplementario es aquel que, sumado a otro ángulo, resulta en una medida de 180 grados.
Por ejemplo:
- Si un ángulo A mide 120 grados, su ángulo suplementario sería de 60 grados, ya que 120 + 60 = 180.
- Si un ángulo B mide 45 grados, su ángulo suplementario sería de 135 grados, ya que 45 + 135 = 180.
En resumen, un ángulo suplementario es aquel cuya medida, sumada a la de otro ángulo, resulta en una medida de 180 grados. Es importante tener en cuenta que los ángulos suplementarios no necesariamente tienen la misma forma o posición.
Propiedad de la suma de dos ángulos suplementarios
La propiedad de la suma de dos ángulos suplementarios establece que la suma de dos ángulos suplementarios siempre es igual a 180 grados.
Para entender mejor esta propiedad, recordemos que dos ángulos son suplementarios cuando la suma de sus medidas es igual a 180 grados. Por ejemplo, si tenemos un ángulo A y otro ángulo B, y la medida del ángulo A es de 120 grados, entonces la medida del ángulo B será de 60 grados, ya que 120 + 60 = 180.
En resumen, la propiedad de la suma de dos ángulos suplementarios establece que la suma de las medidas de dos ángulos suplementarios será siempre igual a 180 grados.
Ejemplo de suma de dos ángulos suplementarios
Los ángulos suplementarios son dos ángulos cuyas medidas suman 180 grados.
Para realizar la suma de dos ángulos suplementarios, simplemente necesitamos conocer el valor de uno de los ángulos y luego restarlo de 180 grados para obtener la medida del otro ángulo.
Ejemplo:
Supongamos que tenemos un ángulo A con medida de 120 grados. Queremos encontrar su ángulo suplementario.
- Conocemos que la suma de dos ángulos suplementarios es igual a 180 grados.
- Restamos la medida del ángulo conocido (120 grados) de 180 grados.
- 180 grados – 120 grados = 60 grados.
Por lo tanto, el ángulo suplementario de 120 grados es de 60 grados.
Este es solo un ejemplo sencillo de cómo se pueden sumar dos ángulos suplementarios. En la práctica, se pueden tener varias combinaciones de medidas de ángulos suplementarios.
Aplicaciones de la suma de dos ángulos suplementarios
La suma de dos ángulos suplementarios tiene diversas aplicaciones en matemáticas y física. Estas aplicaciones se utilizan para resolver problemas geométricos y calcular medidas de ángulos en diferentes contextos.
Una de las aplicaciones más comunes es en trigonometría. En trigonometría, se utilizan los ángulos suplementarios para simplificar ecuaciones y expresiones trigonométricas. Esto permite resolver problemas de geometría y cálculo trigonométrico de manera más eficiente.
En geometría, la suma de dos ángulos suplementarios también se utiliza para demostrar teoremas y propiedades de figuras geométricas. Por ejemplo, en la demostración del teorema de Pitágoras, se utilizan ángulos suplementarios para relacionar las longitudes de los lados de un triángulo rectángulo.
Además, en física, la suma de dos ángulos suplementarios se utiliza para analizar el movimiento de objetos en un plano. Por ejemplo, en cinemática, se utilizan las ecuaciones del movimiento circular uniforme, donde la suma de dos ángulos suplementarios representa el desplazamiento angular de un objeto en movimiento.
Algunas aplicaciones específicas incluyen:
- Cálculo de áreas y perímetros: La suma de dos ángulos suplementarios se utiliza para calcular áreas y perímetros de figuras geométricas como cuadrados, rectángulos y polígonos.
- Resolución de ecuaciones trigonométricas: Las propiedades de los ángulos suplementarios se utilizan para simplificar y resolver ecuaciones trigonométricas más fácilmente.
- Análisis de movimientos: En física, se utilizan los ángulos suplementarios para calcular la velocidad angular y el desplazamiento angular de objetos en movimiento.
En resumen, la suma de dos ángulos suplementarios tiene diversas aplicaciones en matemáticas y física, desde la resolución de ecuaciones trigonométricas hasta el análisis de movimientos y la demostración de teoremas geométricos. Estas aplicaciones son fundamentales para comprender y resolver problemas en diferentes áreas de la ciencia y la matemática.
Conclusiones
En conclusión, luego de analizar detenidamente los datos y argumentos presentados, podemos destacar las siguientes conclusiones:
1. La importancia de las etiquetas HTML
Las etiquetas HTML juegan un papel fundamental en la estructura y diseño de una página web. Proporcionan información semántica y permiten organizar adecuadamente el contenido. Es vital utilizar las etiquetas adecuadas para lograr una correcta visualización y accesibilidad.
2. El uso de H3 para jerarquizar títulos
Los títulos son elementos cruciales en la estructura de un texto. El uso de la etiqueta <h3> permite jerarquizar los diferentes niveles de títulos, lo que facilita la lectura y comprensión del contenido.
3. La utilidad de las listas en HTML
Las listas en HTML resultan muy prácticas para organizar información de manera ordenada. Tanto las listas ordenadas (<ol>) como las listas no ordenadas (<ul>) brindan estructura y mejoran la legibilidad de los contenidos.
4. El énfasis visual mediante negritas
El uso de la etiqueta <b>, que aplica formato en negrita, permite destacar términos clave o frases importantes en un texto. Esta técnica ayuda a captar la atención del lector y resaltar la información esencial.
En resumen, el conocimiento y buen uso de las etiquetas HTML, junto con el aprovechamiento de las opciones de jerarquía y visualización, contribuyen a la creación de páginas web efectivas y atractivas.