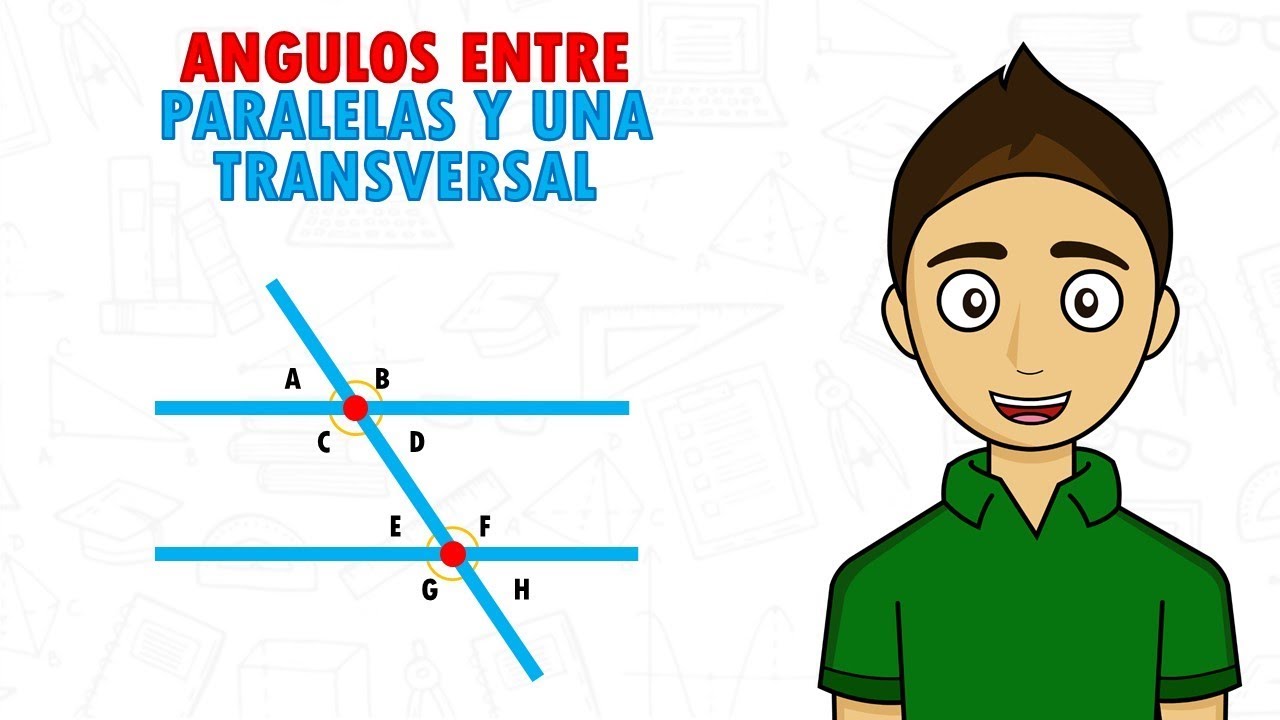
Cuando dos líneas son perpendiculares, se forman varios ángulos interesantes que tienen medidas específicas y propiedades únicas. Vamos a explorar detalladamente estas medidas y propiedades en este artículo.
Propiedades de los ángulos perpendiculares
Al considerar dos líneas que se cruzan de manera que los ángulos adyacentes sean congruentes, es importante entender las medidas y las relaciones de estos ángulos para resolver problemas y aplicar conceptos geométricos en situaciones de la vida real. Así que, comencemos explorando las propiedades y medidas de los ángulos formados por dos líneas perpendiculares.
Ángulos rectos
Los ángulos rectos son fundamentales cuando se trata de líneas perpendiculares, ya que cada par de líneas perpendiculares forma cuatro ángulos rectos. Estos ángulos tienen una medida fija de 90 grados y son cruciales en diversas áreas de las matemáticas y la ingeniería. La importancia de los ángulos rectos radica en su uso en la resolución de problemas geométricos y en la definición de otros tipos de ángulos.
Definición de ángulos agudos
Los ángulos agudos son aquellos que tienen una medida menor a 90 grados y se encuentran en la intersección de las líneas perpendiculares. Son especialmente relevantes en el diseño arquitectónico y en la resolución de problemas geométricos que involucran distancias y proporciones. Comprender la medida de los ángulos agudos es esencial para aplicar conceptos geométricos en situaciones prácticas.
Definición de ángulos obtusos
Los ángulos obtusos tienen una medida mayor a 90 grados y también se forman en la intersección de las líneas perpendiculares. Estos ángulos son fundamentales en la trigonometría y en la resolución de problemas que involucran áreas y volúmenes. Comprender la medida de los ángulos obtusos es crucial para utilizar conceptos geométricos en contextos más complejos.
Relaciones entre ángulos perpendiculares
Las relaciones entre los ángulos formados por líneas perpendiculares son parte integral del campo de la geometría y tienen aplicaciones tanto teóricas como prácticas. Comprender estas relaciones es esencial para resolver problemas geométricos y aplicar conceptos matemáticos en diversas disciplinas.
Ángulos complementarios y suplementarios
La noción de ángulos complementarios y suplementarios es fundamental al considerar líneas perpendiculares. Los ángulos complementarios tienen una suma de 90 grados, mientras que los ángulos suplementarios tienen una suma de 180 grados. Estas relaciones son esenciales en la resolución de problemas de trigonometría y en la definición de diversos conceptos geométricos.
Ángulos opuestos por el vértice
Los ángulos formados en la intersección de las líneas perpendiculares también tienen una relación especial conocida como ángulos opuestos por el vértice. Estos ángulos tienen la misma medida y son fundamentales en la demostración de teoremas geométricos y en la resolución de problemas de congruencia. Comprender esta relación es crucial para aplicar principios geométricos de manera efectiva.
Aplicaciones en la vida cotidiana
Las medidas de los ángulos formados por líneas perpendiculares tienen aplicaciones prácticas en numerosos campos, desde la arquitectura y la ingeniería hasta la cartografía y el diseño de videojuegos. Comprender estas medidas y sus propiedades es fundamental para resolver problemas del mundo real y aplicar conceptos matemáticos en situaciones cotidianas.
Diseño arquitectónico
En el diseño de edificaciones, es fundamental tener en cuenta las medidas de los ángulos formados por las líneas perpendiculares, ya que estas medidas afectan la estabilidad y la distribución del espacio en las estructuras. Comprender la relación entre los ángulos rectos, agudos y obtusos es crucial para diseñar espacios eficientes y estéticamente agradables.
Ingeniería estructural
En la ingeniería estructural, las medidas de los ángulos formados por líneas perpendiculares son esenciales para garantizar la resistencia y estabilidad de las construcciones. El conocimiento de las propiedades de los ángulos complementarios, suplementarios y opuestos por el vértice es fundamental para diseñar estructuras seguras y funcionales.
Cartografía y orientación
En la cartografía y la orientación, comprender las medidas de los ángulos rectos y su relación con los ángulos agudos y obtusos es crucial para representar con precisión la ubicación y la dirección en mapas y sistemas de navegación. Estas medidas son fundamentales para la creación de representaciones exactas de espacios geográficos.
Diseño de videojuegos
En el diseño de videojuegos, las medidas de los ángulos perpendiculares son esenciales para crear entornos virtuales realistas y sistemas de movimiento precisos. Comprender la relación entre los ángulos rectos, agudos y obtusos es crucial para diseñar escenarios y mecánicas de juego que brinden una experiencia inmersiva a los jugadores.
En resumen, las medidas de los ángulos formados por dos líneas perpendiculares tienen propiedades únicas y aplicaciones significativas en diversos campos. Comprender estas medidas es esencial para resolver problemas geométricos y aplicar conceptos matemáticos en situaciones cotidianas y profesionales. Al dominar las propiedades y relaciones de los ángulos perpendiculares, podemos aprovechar su potencial en el diseño, la ingeniería, la navegación y el entretenimiento digital, entre otros campos.