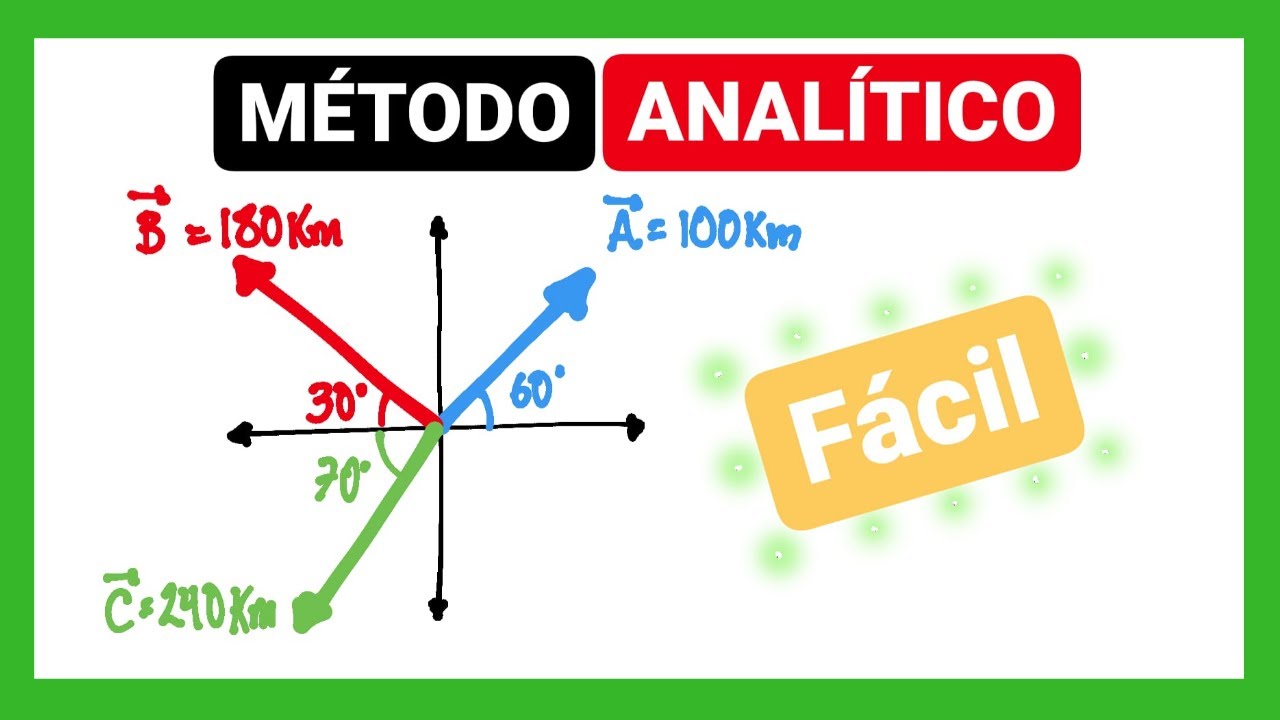
La suma de vectores es un concepto fundamental en física y matemáticas, que se utiliza para encontrar la magnitud y dirección resultante de dos o más vectores. Existen varios métodos para realizar esta operación, y uno de los más utilizados es el método analítico. En este artículo, exploraremos en detalle el método analítico para la suma de vectores, paso a paso, para comprender su aplicación en diferentes contextos.
Para comprender el método analítico para la suma de vectores, es importante tener un sólido conocimiento de los sistemas de coordenadas, componentes de vectores y operaciones matemáticas básicas. Con estos conceptos en mente, podemos seguir adelante y desglosar el proceso analítico para la suma de vectores.
Descomposición de vectores en componentes rectangulares
El primer paso en el método analítico es descomponer los vectores dados en sus componentes rectangulares. Si tenemos un vector en un plano cartesiano, este puede ser descompuesto en dos componentes, generalmente horizontal (x) y vertical (y). Esta descomposición nos permitirá trabajar con las componentes individuales de los vectores, lo que simplificará el proceso de suma.
Componentes rectangulares
Las componentes rectangulares de un vector se pueden encontrar mediante el uso de funciones trigonométricas como el coseno y el seno. Si conocemos el ángulo que el vector forma con el eje x, y su magnitud, podemos calcular fácilmente sus componentes horizontal (x) y vertical (y) utilizando estas funciones trigonométricas.
Notación vectorial
La notación vectorial es crucial en el método analítico. Utilizamos letras minúsculas en negrita para representar vectores, como a → y b →. Al descomponer un vector en sus componentes rectangulares, utilizamos el formato (ax, ay) para denotar las componentes horizontal y vertical, respectivamente.
Suma de componentes
Una vez que tengamos las componentes rectangulares de todos los vectores involucrados, podemos proceder a sumar las componentes horizontal y vertical por separado. Esto nos dará las componentes de la suma resultante, que luego podemos combinar para obtener el vector de suma.
Suma de componentes horizontal
Para sumar las componentes horizontales de los vectores, simplemente sumamos todas las componentes horizontales individuales. Esto nos dará la componente horizontal de la suma resultante.
Suma de componentes vertical
De manera similar, para sumar las componentes verticales de los vectores, sumamos todas las componentes verticales individuales. Esto nos dará la componente vertical de la suma resultante.
Obtención del vector resultante
Una vez que hayamos calculado las componentes de la suma resultante, podemos combinar estas componentes para obtener el vector de suma. Utilizamos estas componentes para formar un nuevo vector, cuyo punto de inicio se encuentra en el origen del sistema de coordenadas, y su extremo coincide con las componentes de la suma resultante.
Magnitud y dirección
La magnitud del vector resultante se puede encontrar utilizando el teorema de Pitágoras en el triángulo formado por las componentes horizontal y vertical. La dirección se puede obtener utilizando funciones trigonométricas, como el ángulo tangente. Estas dos características son vitales para comprender completamente la naturaleza de la suma de vectores.
Ejemplos y aplicaciones
El método analítico para la suma de vectores se aplica en una amplia gama de contextos, desde la física fundamental hasta la ingeniería avanzada. Los conceptos discutidos anteriormente tienen aplicaciones prácticas en problemas de movimiento de partículas, análisis de fuerzas en estructuras y diseño de sistemas complejos que involucran múltiples fuerzas.
Problemas de movimiento bidimensional
En el análisis de movimiento de partículas en dos dimensiones, la suma de vectores es esencial para encontrar la velocidad resultante, aceleración y trayectoria de un objeto en movimiento. El método analítico nos permite descomponer las fuerzas y velocidades en componentes manejables, facilitando el cálculo de la resultante.
Análisis de fuerzas estructurales
En la ingeniería estructural, la suma de vectores se utiliza para calcular las fuerzas resultantes en diferentes partes de una estructura, lo que es fundamental para garantizar la estabilidad y seguridad de una construcción. Al descomponer las fuerzas en sus componentes, podemos evaluar la magnitud y dirección de las fuerzas resultantes.
El método analítico para la suma de vectores es una herramienta poderosa que nos permite comprender y calcular la resultante de múltiples vectores de manera eficiente. Al descomponer los vectores en sus componentes rectangulares, sumar estas componentes y luego formar el vector resultante, podemos abordar una amplia gama de problemas en física y matemáticas con mayor claridad y precisión.
Al comprender y dominar este método, los estudiantes y profesionales pueden desarrollar una comprensión más profunda de los conceptos vectoriales y aplicarlos con confianza en diversas situaciones del mundo real.