«`html
Para calcular el área de un cuadrilátero no regular, es crucial entender sus propiedades y cómo se relacionan las diferentes medidas dentro de la figura. En este artículo, exploraremos un método paso a paso para calcular el área de un cuadrilátero no regular, brindando una comprensión clara y detallada para que puedas aplicarlo en cualquier contexto.
Entendiendo la geometría del cuadrilátero no regular
Antes de sumergirnos en el cálculo del área, es esencial comprender la estructura y las características de un cuadrilátero no regular. A diferencia de un cuadrado o un rectángulo, un cuadrilátero no regular no posee lados iguales ni ángulos rectos. Esta diversidad de longitudes y ángulos lo hace desafiante a la hora de calcular su área, pero con el enfoque adecuado, es factible obtener el resultado.
Identificando los lados y ángulos
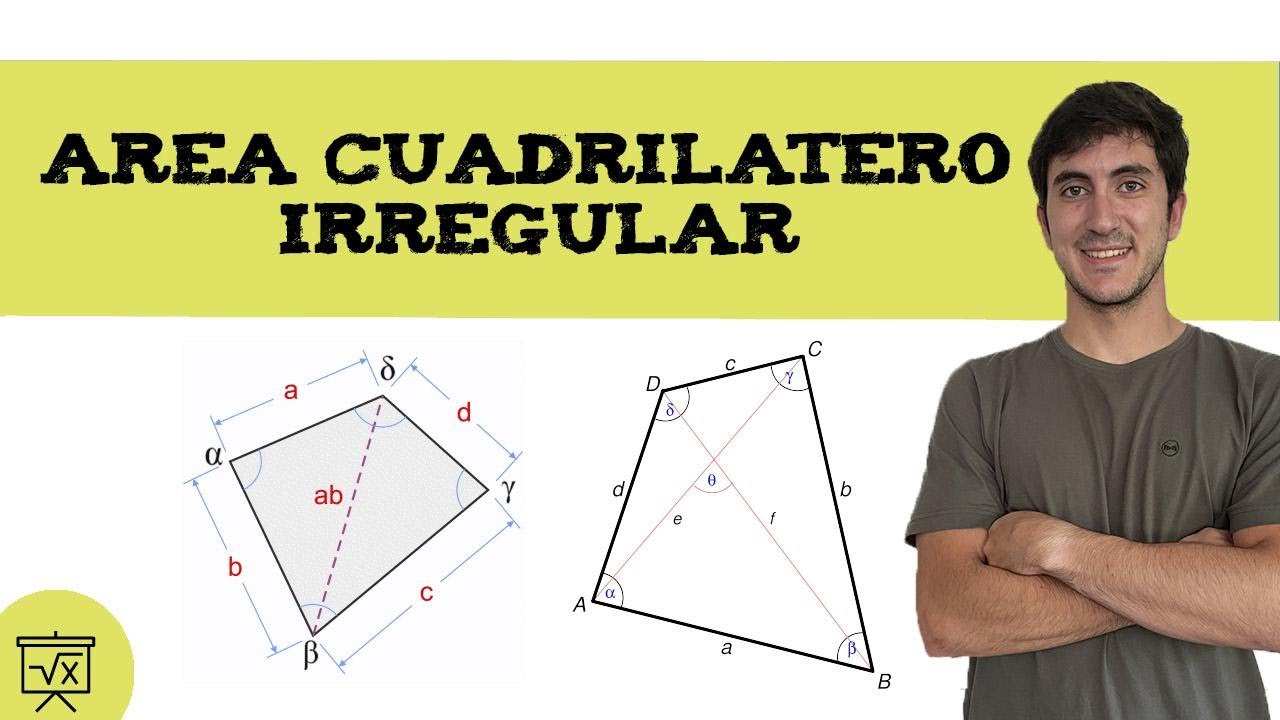
El primer paso para calcular el área de un cuadrilátero no regular es identificar y medir los lados y ángulos relevantes. Utiliza una regla o un instrumento de medición para obtener las longitudes de los lados y un transportador para medir los ángulos con precisión. Anota cuidadosamente estos valores, ya que serán fundamentales en el proceso de cálculo.
Cálculo del área utilizando la fórmula de Brahmagupta
Una vez que hayas reunido los datos necesarios sobre los lados y ángulos, puedes proceder a utilizar la fórmula de Brahmagupta para calcular el área del cuadrilátero no regular. Esta fórmula es especialmente útil para cuadriláteros cuyos lados y ángulos no son uniformes, proporcionando un enfoque integral para obtener el área de la figura.
Conocimiento de la fórmula de Brahmagupta
La fórmula de Brahmagupta para el área de un cuadrilátero no regular se basa en los lados y las semiperímetros de la figura. Para un cuadrilátero con lados de longitud a, b, c, y d, y semiperímetros s1, s2, s3, y s4, la fórmula se expresa como: Área = √(s – a)(s – b)(s – c)(s – d), donde s = (s1 + s2 + s3 + s4) / 2.
Implementación de la fórmula en el cálculo del área
Una vez que has calculado los semiperímetros utilizando la longitud de los lados del cuadrilátero, puedes aplicar la fórmula de Brahmagupta para obtener el área. Asegúrate de reemplazar los valores correspondientes en la fórmula y realizar los cálculos de forma precisa para obtener el área final del cuadrilátero no regular.
Consideraciones adicionales
Es importante recordar que el método de la fórmula de Brahmagupta es aplicable específicamente a cuadriláteros no regulares, y su uso se justifica cuando otros métodos de cálculo resultan inadecuados debido a la complejidad de la figura. Además, la precisión en la medición de los lados y ángulos es crucial para obtener un resultado confiable al aplicar esta fórmula.
Verificación de los resultados
Una vez que hayas calculado el área utilizando el método de la fórmula de Brahmagupta, es recomendable verificar los resultados. Puedes comparar tus cálculos con los de otras fórmulas para calcular áreas de cuadriláteros, como el método de coordenadas o la fórmula de Herón, para confirmar la precisión de tus hallazgos.
Aplicaciones prácticas
Comprender cómo calcular el área de un cuadrilátero no regular es fundamental en diversas disciplinas, incluyendo la arquitectura, la cartografía, y la ingeniería. Este conocimiento puede aplicarse en la determinación de espacios y terrenos no convencionales, así como en el diseño y la planificación de estructuras complejas.
Integración de software de diseño asistido por computadora
En entornos de diseño asistido por computadora (CAD), el cálculo preciso del área de cuadriláteros no regulares es esencial para la generación de modelos tridimensionales y planos de construcción. Los profesionales que trabajan con software de CAD pueden beneficiarse de comprender y aplicar métodos como la fórmula de Brahmagupta para obtener resultados exactos en sus proyectos.
Calcular el área de un cuadrilátero no regular puede presentar desafíos, pero con un enfoque sistemático y la aplicación de fórmulas como la de Brahmagupta, es posible obtener resultados precisos. La comprensión de las propiedades geométricas del cuadrilátero y la precisión en la medición son fundamentales para realizar cálculos confiables y aplicar este conocimiento en diversas áreas profesionales.
«`