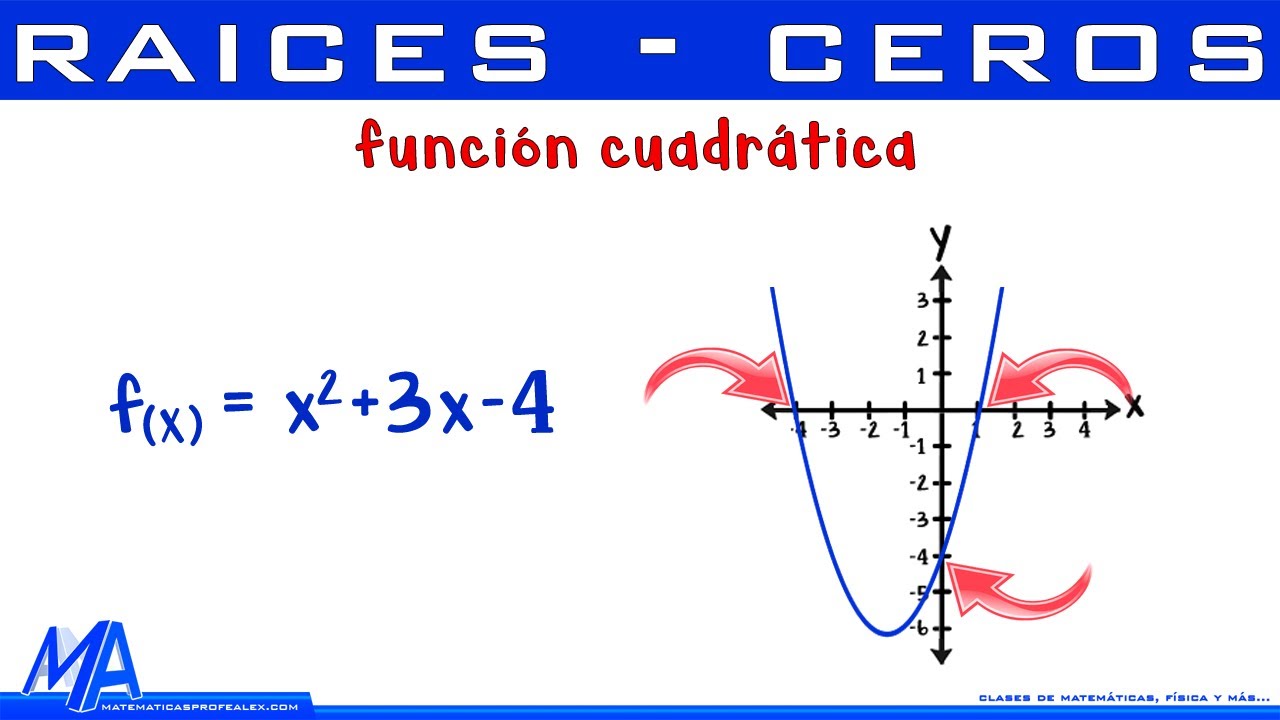
¿Qué es una función cuadrática?
Una función cuadrática es un tipo de función matemática que se caracteriza por tener un término de grado 2, es decir, su ecuación tiene la forma f(x) = ax^2 + bx + c, donde a, b y c son constantes.
La función cuadrática tiene forma de parábola y su gráfica siempre es simétrica respecto a un eje vertical llamado eje de simetría. El vértice de la parábola se encuentra precisamente en el punto medio de este eje.
El coeficiente “a” en la ecuación de la función cuadrática determina si la parábola se abre hacia arriba (si a > 0) o hacia abajo (si a < 0). Si a ≠ 0, la concavidad de la parábola es constante.
Al analizar una función cuadrática, se pueden determinar diferentes características, como el vértice, la concavidad, la intersección con el eje x (raíces) y el punto de intersección con el eje y. Estas características son útiles para comprender el comportamiento de la función en un contexto dado.
Las funciones cuadráticas son ampliamente utilizadas en diversas áreas, como la física, la economía y la ingeniería. Además, su estudio y comprensión son fundamentales en el álgebra y el cálculo.
En resumen, una función cuadrática es una función matemática de segundo grado que tiene la forma f(x) = ax^2 + bx + c. Esta función se representa mediante una parábola y tiene diversas características que permiten analizar su comportamiento en un contexto dado.
Definición de raíz de una función cuadrática
Una raíz de una función cuadrática es un valor en el cual la función se iguala a cero. En otras palabras, es el valor de x que hace que la función cuadrática corte o intersecte el eje x en el plano cartesiano. Estas raíces también son conocidas como ceros, puntos de intersección o soluciones de la función.
La fórmula cuadrática permite encontrar las raíces de una función cuadrática. Esta fórmula, también conocida como la fórmula general, es:
x = (-b ± √(b^2 – 4ac)) / (2a)
Donde a, b y c son los coeficientes de la función cuadrática:
- a es el coeficiente cuadrático.
- b es el coeficiente lineal.
- c es el término independiente o constante.
Las raíces de una función cuadrática pueden ser reales o imaginarias. Cuando el discriminante (b^2 – 4ac) es mayor o igual a cero, las raíces son reales. Si el discriminante es menor que cero, las raíces son imaginarias.
Es importante mencionar que una función cuadrática puede tener dos raíces reales distintas, dos raíces reales iguales o dos raíces imaginarias conjugadas, dependiendo del valor del discriminante.
En conclusión, las raíces de una función cuadrática son los valores de x en los cuales la función se iguala a cero. Estas raíces se pueden encontrar utilizando la fórmula cuadrática y pueden ser reales o imaginarias dependiendo del discriminante de la función.
¿Cuántas raíces puede tener una función cuadrática?
Una función cuadrática puede tener 0, 1 o 2 raíces.
El número de raíces de una función cuadrática está determinado por el discriminante, que se obtiene al evaluar la expresión dentro de la raíz cuadrada en la fórmula general:
𝑥 = (−𝑏 ± √(𝑏^2 − 4𝑎𝑐)) / (2𝑎)
Si el discriminante es mayor que 0, la función tiene dos raíces reales distintas. Si el discriminante es igual a 0, la función tiene una única raíz real. Y si el discriminante es menor que 0, la función no tiene raíces reales.
Por lo tanto, podemos concluir que una función cuadrática puede tener 0, 1 o 2 raíces, dependiendo del valor del discriminante.
Cálculo del número de raíces
En el ámbito de las matemáticas, el cálculo del número de raíces de una función es una tarea crucial. Las raíces de una función son aquellos valores de la variable independiente que hacen que la función se anule, es decir, que el valor de la función sea igual a cero.
Una forma común de calcular el número de raíces de una función es utilizando el Teorema de Bolzano. Este teorema establece que si una función es continua en un intervalo cerrado [a, b] y toma valores de signos opuestos en los extremos del intervalo, entonces existe al menos un valor de la variable independiente dentro del intervalo donde la función se anula.
Para utilizar el Teorema de Bolzano, es necesario encontrar los valores de la función en los extremos del intervalo y verificar si tienen signos opuestos. Si esto se cumple, podemos concluir que existe al menos una raíz en el intervalo.
Además del Teorema de Bolzano, existen otros métodos numéricos para calcular las raíces de una función, como el método de Newton-Raphson o el método de bisección. Estos métodos son algoritmos que nos permiten encontrar de manera aproximada las raíces de una función, incluso cuando no es posible calcularlas de forma exacta.
Ejemplo:
Supongamos que queremos calcular el número de raíces de la función f(x) = x^2 – 4 en el intervalo [-3, 3].
Primero, evaluamos la función en los extremos del intervalo:
- f(-3) = (-3)^2 – 4 = 5
- f(3) = (3)^2 – 4 = 5
Como los valores de la función en los extremos tienen el mismo signo (positivo), no podemos aplicar el Teorema de Bolzano en este caso. Sin embargo, podemos observar que la función es una parábola con concavidad hacia arriba, por lo que sabemos que tiene al menos una raíz.
Utilizando métodos numéricos, podemos encontrar aproximaciones de las raíces de la función. Por ejemplo, aplicando el método de Newton-Raphson, podemos encontrar que una de las raíces de la función es x ≈ -2.
En resumen, el cálculo del número de raíces de una función es una tarea importante en el campo de las matemáticas. Existen diferentes métodos numéricos y teoremas que nos permiten determinar el número de raíces de una función y encontrar aproximaciones de dichas raíces.
Ejemplos de funciones cuadráticas y sus raíces
En matemáticas, una función cuadrática es aquella que puede ser descrita por una ecuación de la forma y = ax^2 + bx + c, donde a, b y c son constantes. Estas funciones se caracterizan por tener una gráfica en forma de parábola.
Función cuadrática: y = 2x^2 – 3x + 1
Este es un ejemplo de una función cuadrática. Los coeficientes son a = 2, b = -3 y c = 1. Para encontrar las raíces de esta función, utilizamos la fórmula general conocida como la fórmula cuadrática.
La fórmula cuadrática establece que las raíces de una función cuadrática están dadas por la fórmula x = (-b ± √(b^2 – 4ac))/(2a).
Aplicando esta fórmula a nuestra función cuadrática, obtenemos:
x = (-(-3) ± √((-3)^2 – 4(2)(1)))/(2(2))
x = (3 ± √(9 – 8))/(4)
x = (3 ± √(1))/(4)
Por lo tanto, las raíces de la función cuadrática son x = (3 + 1)/4 = 1 y x = (3 – 1)/4 = 1/2.
Función cuadrática: y = -x^2 + 5x – 6
Este es otro ejemplo de una función cuadrática. Los coeficientes son a = -1, b = 5 y c = -6. Aplicando la fórmula cuadrática, obtenemos:
x = (-(5) ± √((5)^2 – 4(-1)(-6)))/(2(-1))
x = (-5 ± √(25 – 24))/(-2)
x = (-5 ± √(1))/(-2)
Las raíces de esta función cuadrática son x = (-5 + 1)/(-2) = 2 y x = (-5 – 1)/(-2) = 3.
Como podemos ver en estos ejemplos, las funciones cuadráticas pueden tener dos raíces reales, una raíz única o ninguna raíz real dependiendo del discriminante de la fórmula cuadrática. El discriminante (b^2 – 4ac) determina la naturaleza y cantidad de raíces de la función cuadrática.
Espero que estos ejemplos hayan ayudado a comprender las funciones cuadráticas y cómo encontrar sus raíces.