Comprender la función coseno
La función coseno es un concepto fundamental en matemáticas que representa la relación entre los lados de un triángulo rectángulo y sus ángulos. Su comportamiento se extiende más allá de las figuras geométricas, ya que es una función periódica que se repite a lo largo de la recta real. En este artículo, exploraremos en detalle el rango de la función coseno y desentrañaremos sus valores característicos.
Definición de la función coseno
El coseno de un ángulo en un triángulo rectángulo se define como la razón entre la longitud del cateto adyacente y la hipotenusa. Matemáticamente, se expresa como cos(θ) = adyacente / hipotenusa. Esta definición es fundamental para comprender cómo varían los valores de la función coseno en diferentes contextos.
El rango de la función coseno
El rango de la función coseno se refiere a los valores posibles que puede tomar. Dado que el coseno es una función continua y periódica, su rango se extiende a lo largo de todo el intervalo [-1, 1].
Rango estándar de la función coseno
En el rango estándar de la función coseno, los valores oscilan entre -1 y 1. Es importante destacar que el coseno alcanza su valor máximo de 1 cuando el ángulo es 0 grados, y su valor mínimo de -1 cuando el ángulo es 180 grados. Esto representa un ciclo completo de la función coseno en el intervalo de 0 a 360 grados, o de 0 a 2π radianes.
Variaciones en el rango de la función coseno
A pesar de su rango estándar, la función coseno puede experimentar variaciones cuando se combinan con otras operaciones matemáticas, como transformaciones lineales o composiciones con otras funciones. Estas variaciones pueden extender su rango más allá de los límites tradicionales, lo que resulta en una mayor diversidad de valores posibles.
Aplicaciones del rango de la función coseno
El conocimiento del rango de la función coseno es fundamental en numerosos campos, incluyendo la física, la ingeniería, la informática y la economía. En la física, por ejemplo, el coseno se utiliza para modelar fenómenos ondulatorios, como el movimiento armónico simple. En la ingeniería, la función coseno es esencial para analizar circuitos eléctricos de corriente alterna. En la informática, se aplica en algoritmos de gráficos por computadora y en la interpolación de datos. En la economía, se utiliza para modelar el comportamiento cíclico de los mercados. En cada uno de estos contextos, comprender el rango de la función coseno es crucial para realizar cálculos precisos y extraer conclusiones significativas.
Gráfica del rango de la función coseno
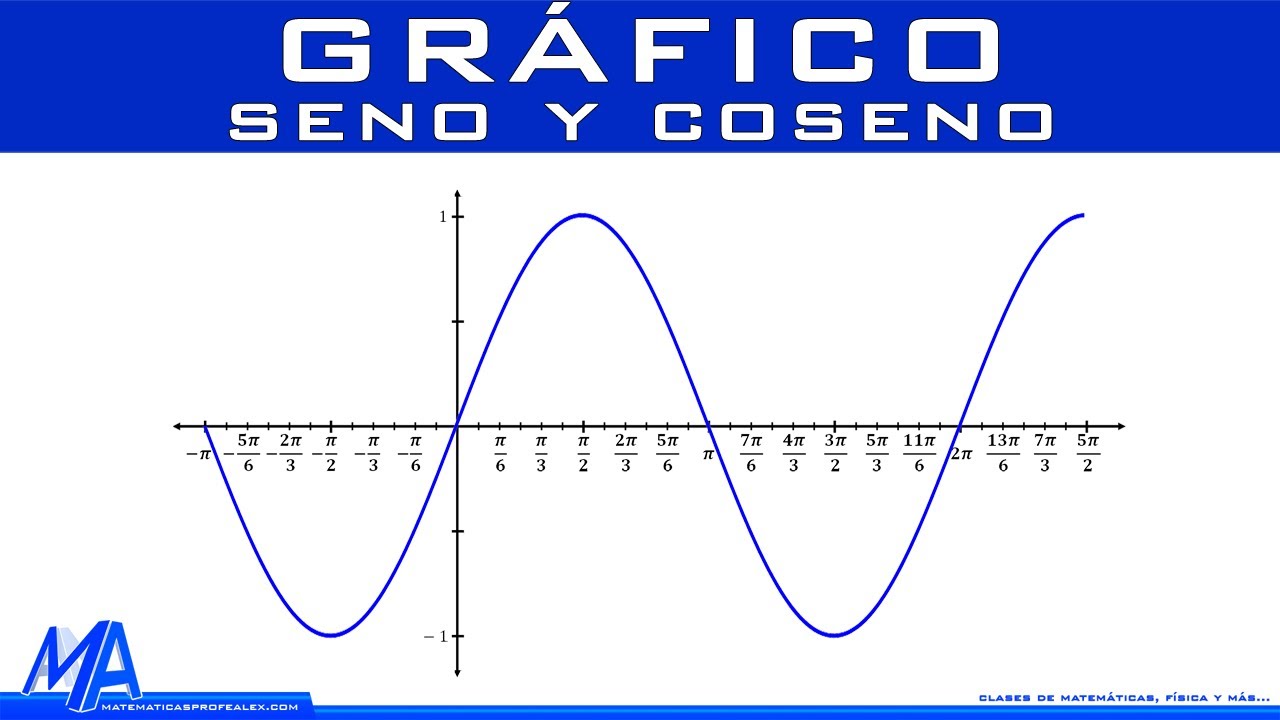
Una forma efectiva de visualizar el rango de la función coseno es a través de su gráfica. Al representar la relación entre el ángulo y el valor del coseno en un sistema de coordenadas, se obtiene una curva suave que oscila entre -1 y 1 a medida que el ángulo varía. Esta representación gráfica proporciona una perspectiva intuitiva del rango de la función coseno y su comportamiento periódico.
Características de la gráfica del coseno
La gráfica del coseno exhibe varias características distintivas que reflejan su rango y patrón repetitivo. La curva oscila simétricamente alrededor del eje horizontal, ya que el coseno es una función par. Además, presenta puntos de inflexión en los valores medios de cada período, lo que marca los puntos de transición entre el crecimiento y la decrecimiento de la función.
Transformaciones de la gráfica del coseno
Mediante la aplicación de transformaciones como el desplazamiento, la compresión o la reflexión, es posible alterar la gráfica estándar del coseno y modificar su rango de valores. Estas transformaciones pueden ampliar la comprensión del comportamiento de la función coseno en diferentes escenarios y su impacto en el rango resultante.
Relación con otras funciones trigonométricas
La función coseno está estrechamente relacionada con otras funciones trigonométricas, como el seno y la tangente. Estas relaciones ofrecen una visión más amplia del rango de valores y las interacciones entre las funciones. Al explorar estas conexiones, se revelan patrones y propiedades fundamentales de las funciones trigonométricas, enriqueciendo así la comprensión del rango de la función coseno en un contexto más holístico.
Paridad y complementariedad
La paridad del coseno, su relación inversa con la función seno, y su conexión con la tangente y las demás funciones trigonométricas, son aspectos que permiten ampliar la comprensión del rango de la función coseno y sus valores característicos.
Convergencia y divergencia de las series trigonométricas
Explorar la convergencia y divergencia de las series trigonométricas asociadas con el coseno proporciona información valiosa sobre la distribución y el límite de los valores dentro de su rango. Este enfoque ofrece una perspectiva más profunda sobre la forma en que los valores de la función coseno se acumulan o divergen en diferentes contextos y configuraciones matemáticas.
En resumen, el rango de la función coseno abarca un intervalo definido de valores que se extiende a lo largo de toda la recta real. Comprender estos valores, sus variaciones y sus aplicaciones es esencial para el estudio de las matemáticas, la física, la ingeniería y muchos otros campos. Al explorar las propiedades y relaciones de la función coseno con profundidad, se desvela un mundo de patrones y comportamientos que enriquecen nuestra comprensión del universo matemático que nos rodea.