«`html
La recta secante y la tangente son conceptos fundamentales en el cálculo y la geometría analítica. Comprender la relación entre estas dos líneas en una función original es crucial para desarrollar una comprensión profunda de las derivadas y la tasa de cambio en el análisis matemático. En este artículo, exploraremos detenidamente cómo la recta secante y la tangente se relacionan entre sí en el contexto de una función original, y cómo este conocimiento fundamental puede aplicarse en problemas reales y abstracciones matemáticas.
«`
«`html
Definición y concepto de la recta secante
«`
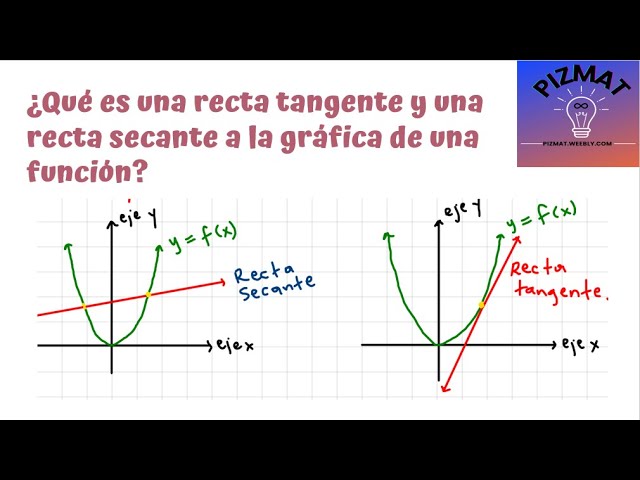
La recta secante es un término utilizado en el campo de la geometría y el cálculo para describir una línea que cruza una curva en al menos dos puntos. Más específicamente, en el contexto de una función matemática, la recta secante es una línea que intersecta a una curva en dos puntos distintos. Esto significa que toca la curva en dos lugares, lo que nos permite calcular la pendiente entre esos dos puntos y comprender mejor el comportamiento de la función en ese intervalo.
La pendiente de la recta secante entre dos puntos específicos en una función original nos proporciona una medida de la tasa de cambio promedio de la función en ese intervalo. Este concepto es fundamental para el desarrollo del cálculo y la comprensión de cómo las funciones cambian a lo largo de diferentes intervalos. La recta secante, por lo tanto, nos permite aproximarnos al comportamiento de la función entre dos puntos específicos, lo que es esencial para comprender la relación entre la recta secante y la tangente.
«`html
Definición y concepto de la tangente
«`
La tangente, por otro lado, es una línea que toca una curva en un solo punto, conocido como el punto de tangencia. En el contexto de una función matemática, la tangente representa la dirección instantánea de cambio de la función en un punto específico. Mientras que la recta secante nos da la tasa de cambio promedio entre dos puntos, la tangente nos proporciona la tasa de cambio instantánea en un punto particular de la función.
La pendiente de la tangente en un punto dado nos indica la tasa de cambio exacta de la función en ese punto, lo que es crucial para comprender el comportamiento local de la función y cómo se acerca a esa ubicación específica. La tangente es fundamental en el cálculo diferencial, ya que nos permite calcular las derivadas de las funciones y comprender cómo cambian en cada punto a lo largo de la curva. Entender la definición y el concepto de la tangente es esencial para apreciar su relación con la recta secante en una función original.
«`html
Relación entre la recta secante y la tangente
«`
La relación entre la recta secante y la tangente en una función original es fundamental para comprender la noción de la derivada y la tasa de cambio en el cálculo diferencial. Al estudiar cómo estas dos líneas se relacionan entre sí, podemos profundizar nuestra comprensión de cómo una función cambia y se comporta en diferentes puntos a lo largo de la curva.
En primer lugar, es importante notar que a medida que los dos puntos de intersección de la recta secante se acercan entre sí, la recta secante se aproxima a la tangente en el punto de tangencia. Esta observación es crucial, ya que nos permite entender intuitivamente cómo la tasa de cambio promedio (representada por la pendiente de la recta secante) se acerca a la tasa de cambio instantánea (representada por la pendiente de la tangente) a medida que los dos puntos de intersección se acercan.
El concepto de límites es esencial para comprender esta relación entre la recta secante y la tangente. La noción de límite nos permite estudiar el comportamiento de una función cuando los dos puntos de intersección de la recta secante se acercan cada vez más, lo que nos proporciona la pendiente de la tangente en el punto de tangencia. Este concepto es crucial para calcular las derivadas de las funciones y entender cómo cambian en cada punto.
Además, la relación entre la recta secante y la tangente nos proporciona un marco conceptual para comprender el concepto de instantaneidad en el cambio. Mientras que la recta secante nos da una idea de cómo cambia la función en un intervalo promedio, la tangente nos proporciona una visión instantánea de cómo se comporta la función en un punto específico. Esta distinción es vital para desarrollar una comprensión profunda de las derivadas y el cambio local en el análisis matemático.
«`html
Aplicaciones prácticas
«`
Comprender la relación entre la recta secante y la tangente en una función original tiene numerosas aplicaciones prácticas en campos como la física, la economía, la ingeniería y la biología. Por ejemplo, en física, la velocidad instantánea de un objeto en movimiento se puede modelar utilizando la tangente a la curva de su posición-tiempo, lo que nos permite calcular la aceleración y comprender mejor su trayectoria. Del mismo modo, en economía, la tasa instantánea de cambio en la demanda o la oferta se puede modelar utilizando la tangente a la curva de la función de demanda o oferta, lo que permite tomar decisiones informadas sobre políticas y estrategias comerciales.
En el campo de la ingeniería, comprender la relación entre la recta secante y la tangente es fundamental para el diseño de estructuras y máquinas, ya que nos permite calcular las velocidades y aceleraciones instantáneas, lo que es crucial para garantizar la seguridad y eficiencia de los sistemas. Incluso en biología, la tasa de crecimiento instantánea de una población se puede modelar utilizando la tangente a la curva de crecimiento, lo que es esencial para comprender las dinámicas de las poblaciones y tomar decisiones informadas sobre conservación y gestión ambiental.
«`html
Desarrollo de la noción de la derivada
«`
La relación entre la recta secante y la tangente en una función original es fundamental para el desarrollo de la noción de la derivada en el cálculo diferencial. La derivada de una función en un punto específico nos da la pendiente de la tangente en ese punto, lo que representa la tasa de cambio instantánea de la función en ese lugar. Al comprender cómo la recta secante se aproxima a la tangente a medida que los dos puntos de intersección se acercan, podemos desarrollar una comprensión profunda de cómo calcular estas pendientes instantáneas y comprender el cambio local en las funciones.
El proceso de encontrar la derivada de una función implica tomar el límite de la pendiente de la recta secante a medida que los puntos de intersección se acercan entre sí, lo que nos proporciona la pendiente de la tangente en el punto de tangencia. Este proceso nos permite determinar cómo cambia la función en cada punto y desarrollar un profundo entendimiento de sus propiedades locales. La derivada es esencial en el cálculo diferencial y nos permite resolver una amplia gama de problemas en matemáticas, física, ingeniería y otros campos.
«`html
Implicaciones teóricas en el análisis matemático
«`
Además de sus aplicaciones prácticas, la relación entre la recta secante y la tangente en una función original tiene profundas implicaciones teóricas en el análisis matemático. Comprender cómo estas dos líneas se relacionan entre sí nos permite profundizar nuestra comprensión de cómo las funciones cambian y se comportan en diferentes puntos a lo largo de la curva, lo que es fundamental para la teoría matemática subyacente.
La relación entre la recta secante y la tangente es esencial para el desarrollo de la teoría de límites en matemáticas, lo que nos permite estudiar el comportamiento de las funciones a medida que los dos puntos de intersección se acercan entre sí. Este concepto es crucial para comprender la continuidad de las funciones, la existencia de las derivadas y el comportamiento local de las curvas, lo que es fundamental para el análisis matemático avanzado y el estudio de funciones más complejas.
Además, la relación entre la recta secante y la tangente nos proporciona un marco teórico para entender el concepto de concavidad y puntos de inflexión en las curvas de las funciones. Al estudiar cómo la recta secante se acerca a la tangente y cómo la pendiente de la tangente cambia en diferentes puntos, podemos desarrollar una comprensión profunda de la curvatura de las funciones y su comportamiento local, lo que es esencial para el análisis gráfico y el estudio de la forma de las curvas.
«`html
«`
En resumen, la relación entre la recta secante y la tangente en una función original es fundamental para el cálculo diferencial, la geometría analítica y el análisis matemático en general. Comprender cómo estas dos líneas se relacionan entre sí nos permite desarrollar una comprensión profunda de la tasa de cambio, la derivada y el comportamiento local de las funciones a lo largo de sus curvas. Esta comprensión no solo tiene aplicaciones prácticas en campos como la física, la economía, la ingeniería y la biología, sino que también tiene profundas implicaciones teóricas en el desarrollo de la matemática como disciplina.
Al estudiar la relación entre la recta secante y la tangente, los estudiantes y los profesionales de las matemáticas pueden desarrollar una apreciación más profunda del cambio y la variación en las funciones, lo que es esencial para la resolución de problemas reales y la comprensión de la teoría subyacente. Esta relación es fundamental en el desarrollo de la noción de la derivada y la comprensión de cómo las funciones cambian en cada punto a lo largo de sus curvas, lo que tiene implicaciones profundas en una amplia gama de disciplinas académicas y prácticas.
Al profundizar en esta relación entre la recta secante y la tangente, los estudiantes y los investigadores pueden fortalecer su comprensión de cómo las funciones se comportan y cambian, lo que es esencial para el avance del conocimiento matemático y su aplicación en el mundo real. Por lo tanto, la relación entre la recta secante y la tangente en una función original es un tema fundamental que merece una atención cuidadosa y una comprensión profunda en el contexto del análisis matemático y sus aplicaciones.