Signos de desigualdad matemática
Las desigualdades son una parte fundamental de las matemáticas y se utilizan para comparar dos cantidades. Los signos de desigualdad nos indican la relación entre dos números y son clave para comprender y resolver problemas matemáticos. Es importante conocer los signos utilizados en las desigualdades y entender su representación gráfica para poder trabajar de manera efectiva con ellas.
Signo de mayor que (>)
El signo de mayor que (>) se utiliza para expresar que un número es mayor que otro. Por ejemplo, si tenemos la desigualdad 5 > 2, esto significa que 5 es mayor que 2. En una representación gráfica, esto se mostraría como una flecha apuntando hacia la derecha, indicando que el número mayor está a la derecha del número menor en una recta numérica.
Signo de menor que (<)
Por otro lado, el signo de menor que (<) se utiliza para expresar que un número es menor que otro. Por ejemplo, la desigualdad 3 < 7 indica que 3 es menor que 7. En la representación gráfica, esto se mostraría como una flecha apuntando hacia la izquierda, indicando que el número menor está a la izquierda del número mayor en la recta numérica.
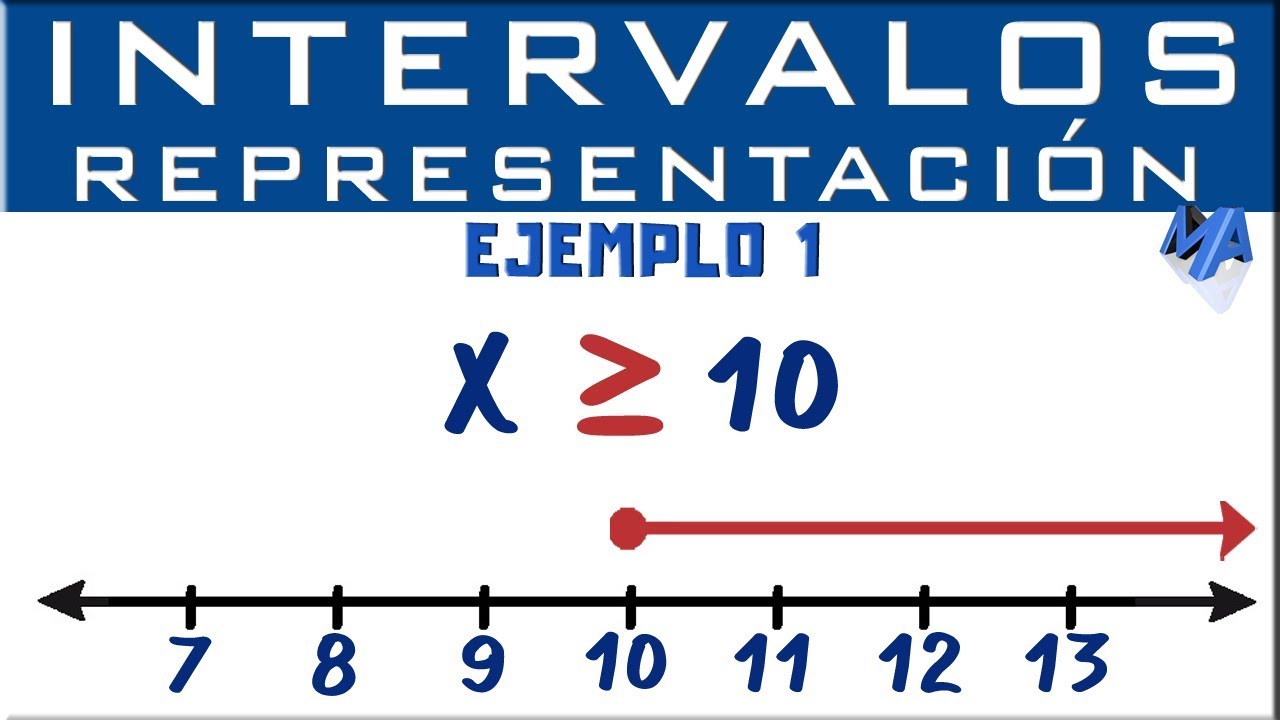
Signo de mayor o igual que (≥)
El signo de mayor o igual que (≥) se utiliza para indicar que un número es mayor o igual que otro. Por ejemplo, la desigualdad 4 ≥ 4 representa que 4 es mayor o igual que 4. En la representación gráfica, esto se mostraría como una línea sólida apuntando hacia la derecha, indicando que el número es igual o mayor que el otro.
Signo de menor o igual que (≤)
Asimismo, el signo de menor o igual que (≤) se usa para expresar que un número es menor o igual que otro. Por ejemplo, la desigualdad 2 ≤ 2 indica que 2 es menor o igual que 2. En la representación gráfica, esto se mostraría como una línea sólida apuntando hacia la izquierda, indicando que el número es igual o menor que el otro.
Resolución de desigualdades lineales
Las desigualdades lineales son expresiones matemáticas en las que se compara una expresión lineal con otra utilizando signos de desigualdad. Para resolver desigualdades lineales, es importante seguir ciertos pasos para encontrar el valor de la variable que satisface la desigualdad.
Paso 1: Simplificar la desigualdad
El primer paso para resolver una desigualdad lineal es simplificar la expresión, tal como se haría al resolver una ecuación. Se pueden combinar términos semejantes y reducir la desigualdad a su forma más simple.
Paso 2: Aislar la variable
Una vez que la desigualdad está simplificada, el siguiente paso es aislar la variable en un lado de la desigualdad. Esto implica realizar operaciones algebraicas para dejar la variable sola en un lado de la desigualdad, de manera similar a como se haría al resolver una ecuación.
Paso 3: Graficar la solución
Una vez que se ha encontrado el valor de la variable que satisface la desigualdad, es útil graficar la solución en una recta numérica. Esto permite visualizar claramente los valores que satisfacen la desigualdad y determinar si se incluyen o no en la solución.
Desigualdades compuestas
Las desigualdades compuestas son expresiones que combinan múltiples desigualdades a través de conectores lógicos como «y» o «o». Resolver desigualdades compuestas implica trabajar con cada desigualdad individual y luego combinar las soluciones de manera apropiada.
Desigualdades con valor absoluto
Las desigualdades que involucran valor absoluto presentan un desafío adicional debido a la naturaleza de la función de valor absoluto. Es necesario considerar los casos en los que el valor dentro del valor absoluto es positivo y negativo para encontrar la solución correcta.
Desigualdades en dos variables
Cuando se trabajan con desigualdades que involucran dos variables, es importante graficar las soluciones en un plano cartesiano para visualizar las regiones que satisfacen la desigualdad. Esto permite identificar claramente las áreas que cumplen con las condiciones establecidas por la desigualdad.
Aplicaciones en la vida cotidiana
Las desigualdades matemáticas tienen aplicaciones en diversos aspectos de la vida cotidiana, desde la planificación de presupuestos hasta la programación de horarios. Comprender cómo representar y resolver desigualdades es fundamental para abordar situaciones del mundo real de manera efectiva.
En resumen, la representación de desigualdades a través de signos matemáticos es esencial para comparar cantidades y resolver problemas en diversos contextos. Desde los signos básicos de mayor que y menor que, hasta la resolución de desigualdades lineales y compuestas, dominar este concepto es fundamental para desarrollar habilidades en matemáticas y aplicarlas en la vida diaria.