1. ¿Qué son las coordenadas de un punto?
Las coordenadas de un punto son un par de valores numéricos que se utilizan para ubicar ese punto en un sistema de coordenadas. Estas coordenadas representan la posición relativa del punto en relación con un origen.
En un sistema de coordenadas bidimensional, las coordenadas de un punto se expresan generalmente como un par ordenado (x, y). El valor de x representa la distancia horizontal desde el origen hasta el punto, mientras que el valor de y representa la distancia vertical.
Por ejemplo, si tenemos un punto P en un sistema de coordenadas y se encuentra a 3 unidades a la derecha del origen y 2 unidades hacia arriba, las coordenadas de ese punto serían (3, 2).
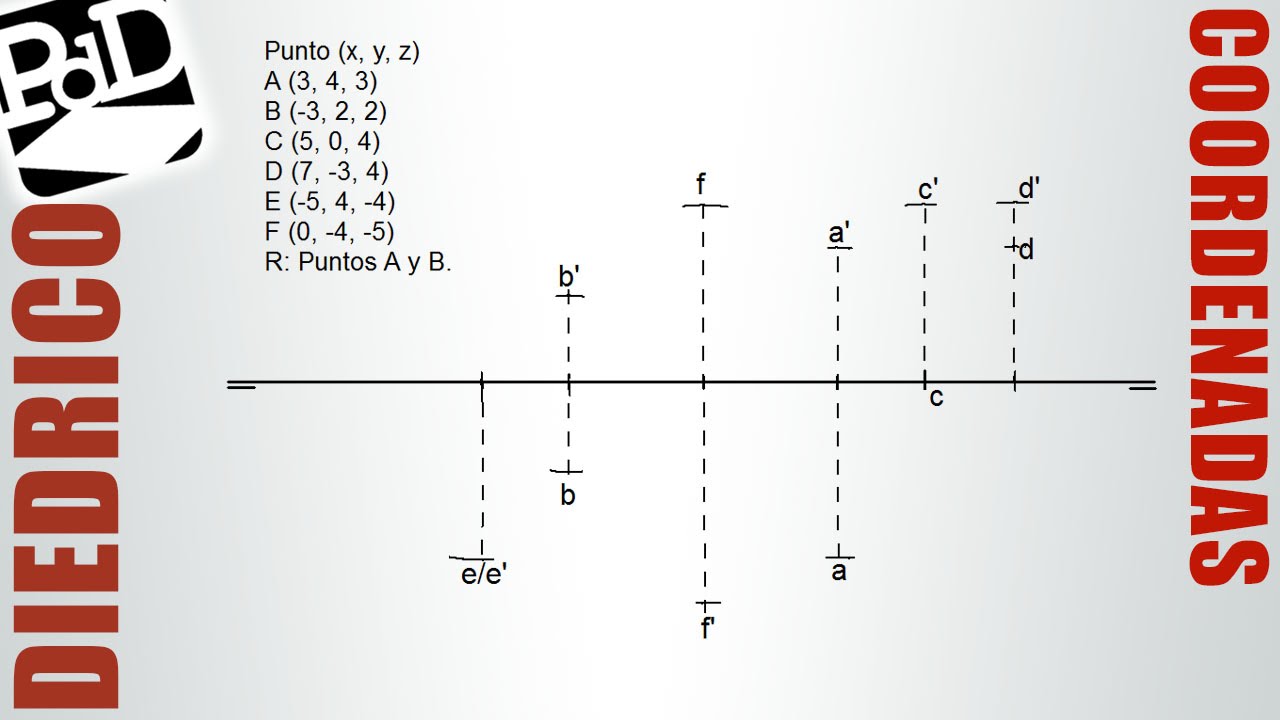
Las coordenadas de un punto también pueden expresarse en un sistema de coordenadas tridimensional, donde se utiliza un par ordenado (x, y, z). El tercer valor, z, representa la distancia del punto al plano de referencia o su altura.
En resumen, las coordenadas de un punto son valores numéricos que nos permiten ubicar ese punto en un sistema de coordenadas, ya sea bidimensional o tridimensional.
2. Sistema de coordenadas cartesianas
El sistema de coordenadas cartesianas es un sistema utilizado en matemáticas y física para ubicar puntos en un plano. Fue desarrollado por el matemático y filósofo francés René Descartes en el siglo XVII.
En este sistema, se utilizan dos líneas perpendiculares: el eje x (también conocido como abscisa) y el eje y (también conocido como ordenada). Estos ejes se cruzan en un punto llamado origen, que se representa como (0, 0). Las coordenadas de un punto en el plano se representan mediante pares ordenados (x, y), donde x representa la posición del punto en el eje x y y representa la posición en el eje y.
El eje x se extiende hacia la derecha de origen, con valores positivos, y hacia la izquierda, con valores negativos. El eje y se extiende hacia arriba desde el origen, con valores positivos, y hacia abajo, con valores negativos. De esta manera, se puede localizar cualquier punto en el plano mediante sus coordenadas cartesianas.
Las coordenadas (x, y) nos permiten medir distancias y ángulos en el plano. Por ejemplo, la distancia entre dos puntos A(x1, y1) y B(x2, y2) se calcula utilizando la fórmula de la distancia euclidiana:
d = √((x2 – x1)^2 + (y2 – y1)^2)
Además, podemos calcular el ángulo formado por dos puntos A(x1, y1) y B(x2, y2) utilizando la fórmula del ángulo:
θ = arctan((y2 – y1)/(x2 – x1))
En resumen, el sistema de coordenadas cartesianas es una herramienta fundamental en matemáticas y física que nos permite representar y ubicar puntos en un plano, y realizar cálculos de distancias y ángulos entre ellos.
3. Sistema de coordenadas polares
El sistema de coordenadas polares es una forma de representar puntos en un plano utilizando una coordenada radial y una coordenada angular. En lugar de utilizar los ejes cartesianos tradicionales, este sistema utiliza un eje central (conocido como polo) y una línea de referencia (conocida como eje polar).
En este sistema, cada punto se representa mediante un par ordenado (r, θ), donde r representa la distancia del punto al polo y θ representa el ángulo formado entre el eje polar y la línea que une el polo con el punto.
La coordenada radial r puede ser positiva o negativa, dependiendo de si el punto se encuentra en el mismo lado o en el opuesto del polo. Por otro lado, el ángulo θ se mide en sentido contrario a las agujas del reloj, comenzando en el eje polar.
Para visualizar mejor el sistema de coordenadas polares, es común utilizar gráficos circulares o diagramas de rosas. En estos gráficos, cada punto se representa mediante un vector que parte del polo y se extiende hacia la dirección y distancia indicadas por las coordenadas r y θ.
Es importante destacar que el sistema de coordenadas polares presenta algunas ventajas y desventajas en comparación con el sistema de coordenadas cartesianas. Por un lado, es especialmente útil para representar formas circulares o simétricas, facilitando la comprensión de ciertos fenómenos físicos y matemáticos.
Por otro lado, este sistema puede resultar más complejo de utilizar en situaciones donde se requiere una representación precisa de la ubicación de los puntos, ya que la medición de distancias y ángulos puede ser más complicada que en el sistema cartesiano.
4. Coordenadas geográficas
Las coordenadas geográficas son un sistema utilizado para localizar cualquier punto en la superficie terrestre. Consisten en dos valores numéricos: la latitud y la longitud.
La latitud se refiere a la distancia que hay desde un punto hasta el ecuador, y se mide en grados. Puede ser norte (+) o sur (-) del ecuador. La latitud máxima es 90 grados y es el Polo Norte, mientras que la latitud mínima es -90 grados y es el Polo Sur.
La longitud es la distancia que hay desde un punto hasta el meridiano de Greenwich, y también se mide en grados. Puede ser este (+) u oeste (-) del meridiano de Greenwich. La longitud máxima es 180 grados y es la línea internacional de cambio de fecha. La longitud mínima es -180 grados, que también es la línea internacional de cambio de fecha.
Para representar las coordenadas geográficas en un mapa, se utilizan las líneas de latitud (también conocidas como paralelos) y las líneas de longitud (también conocidas como meridianos).
Líneas de latitud
Las líneas de latitud se trazan de manera paralela al ecuador, y su valor aumenta o disminuye a medida que te alejas del ecuador. Se utilizan para determinar la distancia norte o sur de un punto en relación al ecuador. Algunas de las líneas de latitud más conocidas son:
- Trópico de Cáncer (23.5° N): se encuentra al norte del ecuador y marca el punto más al norte donde el sol puede estar directamente en el cenit.
- Trópico de Capricornio (23.5° S): se encuentra al sur del ecuador y marca el punto más al sur donde el sol puede estar directamente en el cenit.
- Círculo Polar Ártico (66.5° N): marca el límite más al norte de la zona donde se puede experimentar el fenómeno del sol de medianoche.
- Círculo Polar Antártico (66.5° S): marca el límite más al sur de la zona donde se puede experimentar el fenómeno del sol de medianoche.
Líneas de longitud
Las líneas de longitud se trazan de manera perpendicular al ecuador y se utilizan para determinar la distancia este u oeste de un punto en relación al meridiano de Greenwich. Algunas de las líneas de longitud más conocidas son:
- Meridiano de Greenwich (0°): es la línea de longitud de referencia y separa el hemisferio este y el oeste.
- Meridiano de 180°: es la línea que marca la línea internacional de cambio de fecha, y separa el hemisferio este y el oeste.
- Meridiano de 90° este: divide el hemisferio este en dos partes iguales.
- Meridiano de 90° oeste: divide el hemisferio oeste en dos partes iguales.
En resumen, las coordenadas geográficas son un sistema utilizado para localizar cualquier punto en la superficie terrestre. Las líneas de latitud se utilizan para determinar la ubicación norte o sur de un punto, mientras que las líneas de longitud se utilizan para determinar la ubicación este u oeste de un punto. Estas coordenadas son fundamentales para la cartografía y la navegación, ya que permiten ubicar con precisión cualquier lugar en el mundo.
5. Aplicaciones de las coordenadas de un punto
Las coordenadas de un punto son valores numéricos que permiten ubicar dicho punto en un sistema de coordenadas.
Estas coordenadas son ampliamente utilizadas en diferentes aplicaciones, tanto en la geometría como en la física y la navegación. Algunas de las aplicaciones más comunes son:
- Geolocalización: Las coordenadas son utilizadas para determinar la ubicación exacta de un punto en la Tierra. Esto es especialmente útil en aplicaciones de navegación, como GPS, mapas en línea y aplicaciones de seguimiento en tiempo real.
- Modelado 3D: En software de diseño y modelado en 3D, las coordenadas son esenciales para poder ubicar y posicionar objetos en un espacio tridimensional. Estas coordenadas permiten determinar la posición en el eje x, y, y z de cada punto del modelo.
- Física y matemáticas: En física, las coordenadas son utilizadas para describir la posición de objetos en un sistema de referencia. También se utilizan en cálculos matemáticos complejos, como en el cálculo vectorial y en la geometría analítica.
- Cartografía: En la creación de mapas y planos, las coordenadas son fundamentales para ubicar y representar correctamente cada punto del terreno. Esto permite tener una representación precisa y detallada de un área determinada.
- Robótica y control de movimiento: En el campo de la robótica, las coordenadas se utilizan para controlar los movimientos de los robots. Con las coordenadas, es posible programar y controlar la posición y trayectoria de los robots en un espacio determinado.
En conclusión, las coordenadas de un punto tienen diversas aplicaciones en diferentes áreas, como la geolocalización, el modelado 3D, la física, la cartografía y la robótica. Estas aplicaciones demuestran la importancia de las coordenadas para ubicar y representar puntos en un sistema de referencia.